Время прочтения: 3 мин.
На вход модели могут подаваться следующие виды признаков:
Dj — множество возможных значений для j – ого признака.
- Бинарные признаки: Dj = {0;1}
- Числовые признаки: Dj = R
- Категорийные признаки: Dj = {u1, … , un}, где n — количество категорий
Первые два типа признаков значительно реже требуют обработок чем третий, так как в них чаще всего нет никакой структуры, нам не известно, как та или иная категория влияет на отклик. Поэтому очень полезно перекодировать такие признаки.
На просторах интернета почти всегда предлагают применять к категориальным признакам One-hot encoding, пример применения метода приведен в таблице ниже.
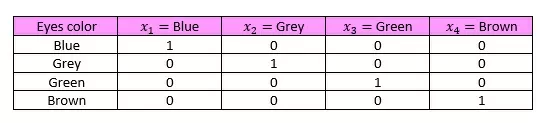
Перед тем как говорит о том, чем плох данный метод в линейных моделях вспомним базовые предположения МНК.
- Линейность отклика: y=Xw + ε
- Случайность выборки: наблюдения (xj, yj)
- Полнота ранга X: ни один из признаков не является линейной комбинацией других признаков
- Случайность ошибок: E(x)=0
При соблюдении всех этих условий мы получаем несмещенные и состоятельные оценки коэффициентов перед регрессорами.
Теперь вспомним, что при построении линейной регрессии в матрицу объектов-признаков мы добавляем столбец из единиц, с помощью которого мы будем учитывать константный признак. Однако после применения One-hot encoding этот столбец будет полностью линейно выразѝм с помощью новых признаков. То есть мы утратим несмещенность и состоятельность оценок коэффициентов, а их дисперсия будет бесконечной. Это не очень удобно при построении доверительных интервалов: это будут доверительные интервалы бесконечной ширины, гипотезы тоже не проверить. Способ избежать этого можно использовать dummy-кодирование, кодировать n-1 переменную, как в таблицу ниже.
Перейдем к практическому примеру, воспользуемся данными из прошлой статьи (ссылка), прологарифмируем totsp, kitsp и целевую переменную price, удалим kitsp. Наша таблица имеет следующий вид.
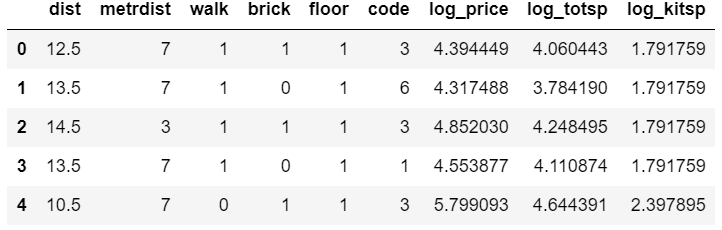
Применим One-hot encoding к признаку code.
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import ColumnTransformer
ohe = ColumnTransformer([("One hot", OneHotEncoder(sparse=False),[5])], remainder="passthrough")
X = ohe.fit_transform(X.drop(columns=['log_price']))
y = df['log_price']
На выходе мы получаем numpy матрицу, у которой первые восемь столбцов соответствуют нашим новым признакам. Обучим модель.
reg = LinearRegression().fit(X, y)
print(reg.intercept_, reg.coef_, reg.score(X, y), sep='\n')

Обратим внимание на значения коэффициентов, уж больно они велики, хоть и качество приемлемое. Попробуем использовать dummy-кодирование.
df['code_1'] = np.where(df['code'] == 1, 1, 0)
df['code_2'] = np.where(df['code'] == 2, 1, 0)
df['code_3'] = np.where(df['code'] == 3, 1, 0)
df['code_4'] = np.where(df['code'] == 4, 1, 0)
df['code_5'] = np.where(df['code'] == 5, 1, 0)
df['code_6'] = np.where(df['code'] == 6, 1, 0)
df['code_7'] = np.where(df['code'] == 7, 1, 0)
X = df.drop(columns=['log_price'])
y = df['log_price']
X.head()
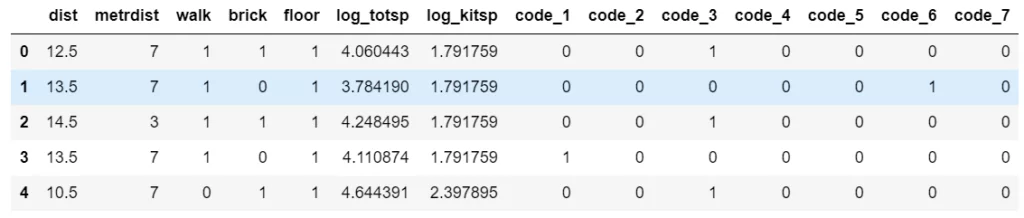
reg = LinearRegression().fit(X, y)
print(reg.intercept_, reg.coef_, reg.score(X, y), sep='\n')
Как видим результат стал значительно лучше, теперь можно проверять гипотезы и получать корректную информацию о влиянии признака на отклик. Важно заметить, что проблема с использованием One-hot encoding в линейных моделях не всегда дает о себе знать, но учитывать риск нужно.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
