Время прочтения: 5 мин.
А что если использовать свои навыки регрессии, чтобы предсказать длину головы опоссума по остальным метриками его тела?
Для тех, кто подзабыл: линейная регрессия— это регрессионная модель, которая позволяет описать зависимость одной переменной от одной или нескольких других переменных с линейной функцией зависимости.
В открытом доступе есть датасет про опоссумов. Для расчёта нужно взять csv-файл, который содержит информацию из девяти метрик каждого из 104 горных кистехвостых опоссумов, отловленных в семи местах от Южной Виктории до центрального Квинсленда.
Необходимо загрузить датасет и проанализировать базу для исследования. Построю модель линейной регрессии с помощью Python. Для этого понадобится несколько библиотек:
- pandas поможет прочитать данные;
- Numpy для обработки данных;
- matplotlib будет отвечать за визуализацию результата;
- Sklearn, statsmodels помогут создать саму модель линейной регрессии.
Описание загрузки библиотек и бинаризации переменных опущу (ссылка на полный код). На выходе получаю следующий датафрейм
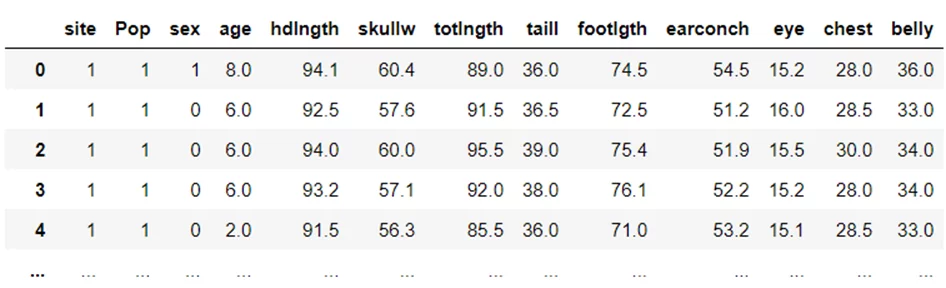
Модель линейной регрессии, которую нужно будет обучить, импортируется с помощью библиотеки sklearn. В качестве X будут выступать метрики, отвечающие за размеры тела опоссума: skullw , totlngth , taill , footlgth , earconch , eye , chest , belly, а в качестве Y – параметр hdlngth.
Нужно нормализовать данные (т. к. линейная регрессия чувствительна к нормализации) и обучить модель.
X = df_possum[['skullw','totlngth','taill','footlgth','earconch','eye','chest','belly']]
y = df_possum['hdlngth']
X = (X - X.mean(axis=0)) / (X.std(axis=0))
X_with_constant = sm.add_constant(X)
X_train, X_test, y_train, y_test = train_test_split(X_with_constant, y, train_size=0.7, random_state = 777)
lr_model_ols = sm.OLS(y_train, X_train).fit()
Модель готова и обучена. Это значит, что получены заветные коэффициенты линейной регрессии, которые позволяют решить задачу по ловле опоссума. Проанализирую параметры модели:
lr_model_ols.summary()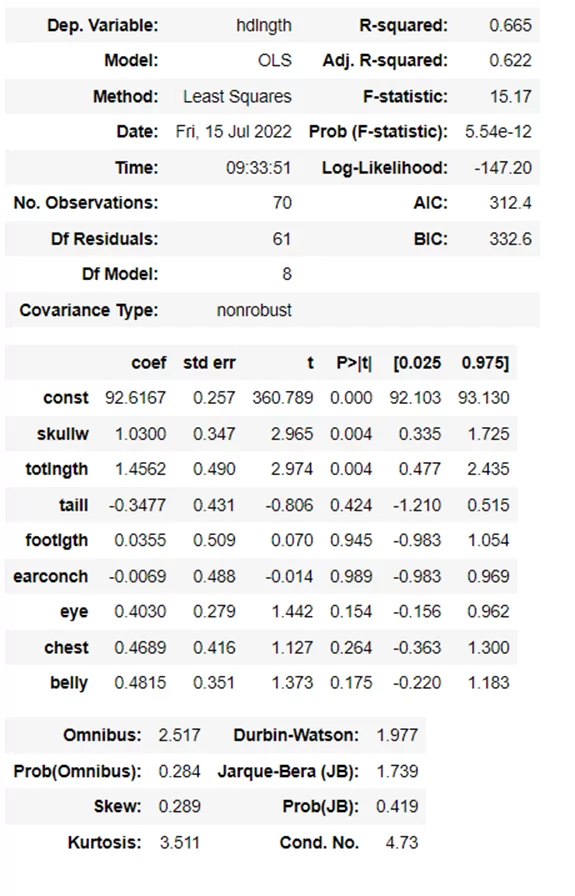
Левый верхний столбец показывает детали, которые уже известны – зависимая переменная, какая модель использовалась, дата, время. Правый столбец отображает статистические критерии – в данном случае наиболее важен второй – adj. R – squared. Этот критерий показывает насколько независимые переменные (показатели размеров тела) объясняют зависимую переменную (местообитания опоссума), в моём случае – на 62%. Другие статистические критерии также важны, про них много написано в интернете.
Теперь перейдём к анализу нижней части – по сути это и есть наша модель. Она показывает коэффициенты в формуле линейной регрессии – то как каждая переменная влияет на изменение зависимой переменной, стандартные отклонения коэффициента. Наиболее важным критерием здесь является P>|t| — это вероятность того, что коэффициент в целом получен случайно, о статистической значимости обычно говорят если этот параметр меньше или равен 0.05. Не все наши переменные удовлетворяют условия, но для обучающей модели подойдут.
Дальше необходимо проанализировать ошибки, коэффициент детерминации и построить гистограмму «важности» признаков. Ошибки показывают насколько «хорошую» модель удалось получить. А гистограмма – какие признаки были наиболее влиятельными в ходе построения решения, иными словами, какие из них наиболее «весомы» в определении места обитания.
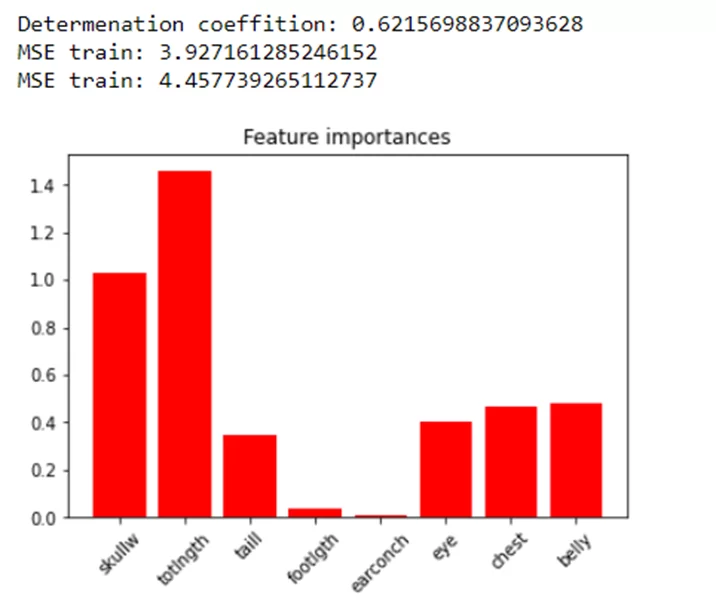
На графике видно, что не все признаки одинаково влияют на выбор модели. Необходимо рекурсивно обучить модель на различном количестве признаков (сортируя по их важности) и посмотреть на ошибки. Часто такой подход помогает избавиться от «лишних» переменных, которые создают шум при построении модели, тем самым ухудшая её качество. Для этого попытаюсь улучшить качество модели, а также сократить время обучения за счёт уменьшения количества признаков.
Код приведён в источнике, получаю такую зависимость

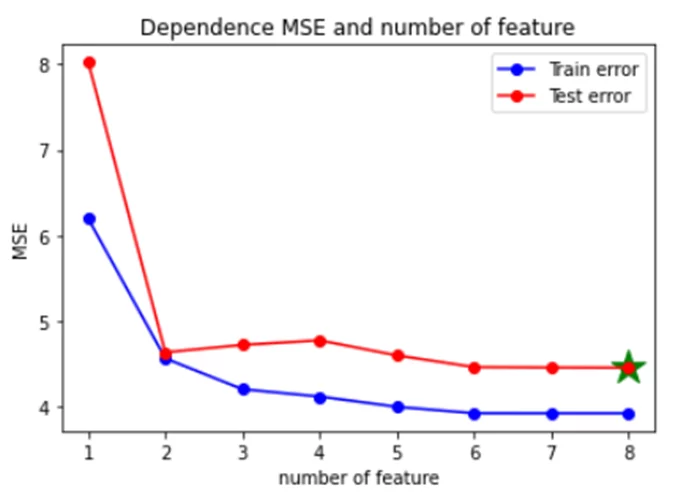
Наименьшая ошибка получилась при 8 признаках из 8. Часто встречаются ситуации, когда 3 или 4 признака показывают себя лучше, чем при использовании всех.
Лучшим выбором при использовании только 1 признака был бы столбец totlngth, если 2 – то skullw , totlngth и т.д. Причем на двух признаках ошибка резко становится меньше.
Теперь попробую обучить модель на 2 лучших признаках и посмотреть, как изменятся ошибки в модели. Код приведён в источнике, получаю такие ошибки

Качество модели не улучшилось, а ошибки стали больше, но уменьшилось время обучения, особенно это заметно на больших датасетах.
Теперь рассмотрю на двух конкретных примерах работу модели:
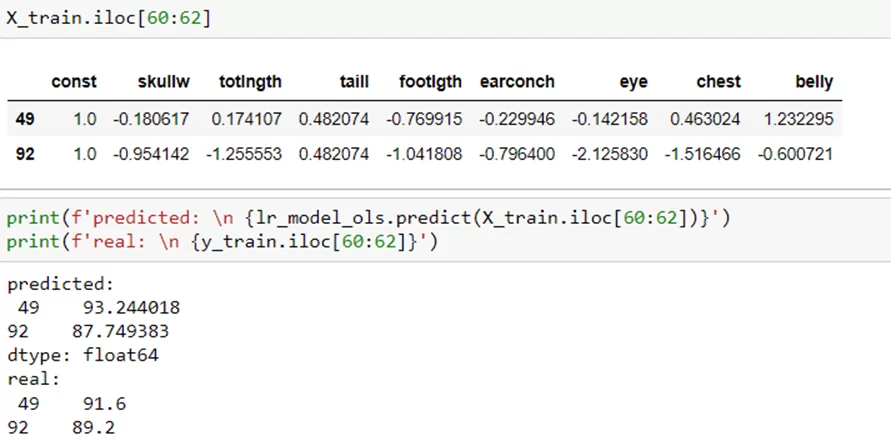
В заключении хотелось бы сказать, что в посте рассмотрен принцип работы линейной регрессионной модели, а также базовое применение и подбор признаков. Однако обучение не ограничивается этим набором. Можно использовать регуляризацию и подбирать коэффициенты для нее для улучшения предсказаний. Ну и конечно необходимо иметь ввиду, что не все данные возможно описать с помощью этой модели, так как не все они являются хорошо линейно разделимыми.
Готовый Jupiter notebook размещен здесь (ссылка на полный код)

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
