Время прочтения: 4 мин.
В качестве примера будем использовать датасет “flats_moscow” с ценами квартир в Москве.
Все квартиры описывается с помощью следующих полей:
- n – порядок квартиры в таблице
- price – стоимость квартиры, тыс. $
- totsp – общая площадь квартиры, кв.м.
- livesp — жилая площадь квартиры, кв.м.
- kitsp – площадь кухни, кв.м.
- dist – расстояние от центра, км.
- metrdist – время до метро, мин.
- walk – 1 – пешком от метро, 0 – на транспорте
- brick 1 – кирпичный, монолит ж/б, 0 – другой
- floor 1 – этаж кроме первого и последнего, 0 – иначе
- code – число от 1 до 8, при помощи которых группируются наблюдения по районам.
При желании можно найти датасет по ссылке. Сейчас не будем задумываться над предобработкой данных и увеличением score, построим классическую модель линейной регрессии.
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
from sklearn.linear_model import LinearRegression
df = pd.read_csv('flats_moscow.txt', sep='\t')
X = df.drop(columns=['n', 'price'])
y = df['price']
reg = LinearRegression().fit(X, y)
Выведем полученные коэффициенты перед регрессорами и (коэф. детерминации).
print(reg.intercept_, reg.coef_, reg.score(X, y), sep='\n')
Построим такую же модель используя библиотеку statsmodels. Основной отличительной чертой является ручное прописывание формулы модели, которую мы хотим получить.
model_1 = smf.ols('price ~ totsp + livesp + kitsp + dist + metrdist +'\
'walk + brick + floor + code', data=df).fit()
Выведем информацию о модели.
print(model_1.summary())Получаем таблицу, обратим внимание на её правую верхнюю часть. R-squred – коэф. детерминации, Adj. R-squred – скорректированный коэф. детерминации, значение F-статистики, проверяющей гипотезу о незначимости модели в целом и её достигнутый уровень значимости, а также информационные критерии AIC, BIC. Ниже находится информация о регрессорах. В столбце coef находятся значения коэффициентов, std err стандартное отклонение коэффициента, t значение t-статистики, проверяющей гипотезу о незначимости признака, R > |t| достигнутый уровень значимости для этой статистики. В последнем столбце находится 95% доверительный интервал для коэффициентов.
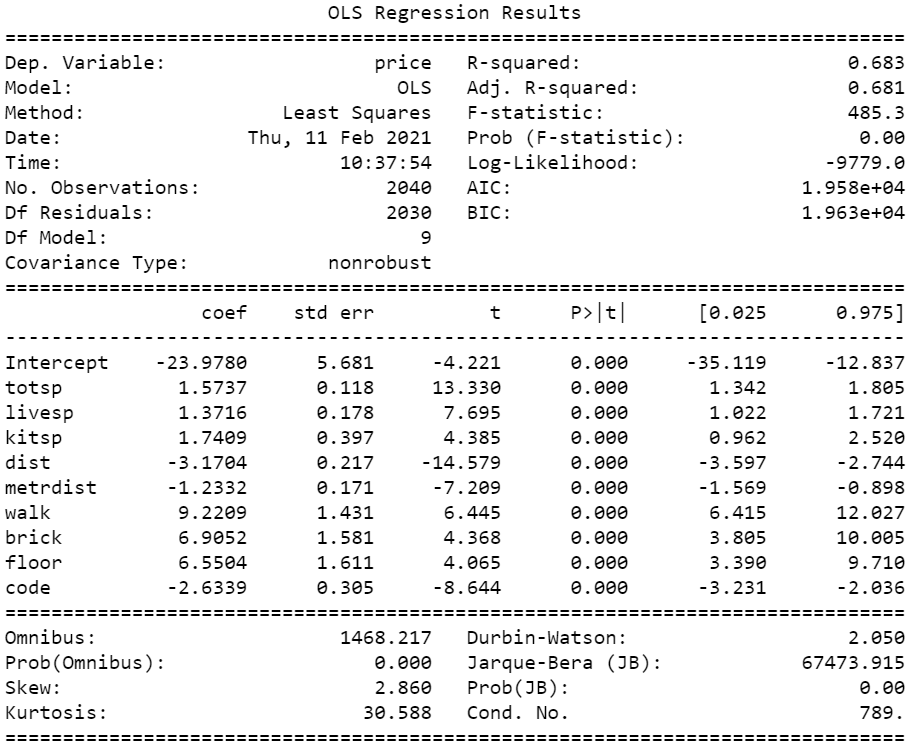
Теперь прологарифмируем totsp, livesp, kitsp и целевую переменную. При использовании sklearn нам бы пришлось отдельно изменять эти признаки, но это долго и муторно. В statsmodel от нас потребуется в строке с формулой явно указать, что мы хотим использовать логарифм признака.
model_2 = smf.ols('np.log(price) ~ np.log(totsp) + np.log(livesp) + np.log(kitsp) + dist +'\
' metrdist + walk + brick + floor + code', data=df).fit()
print(model_2.summary())
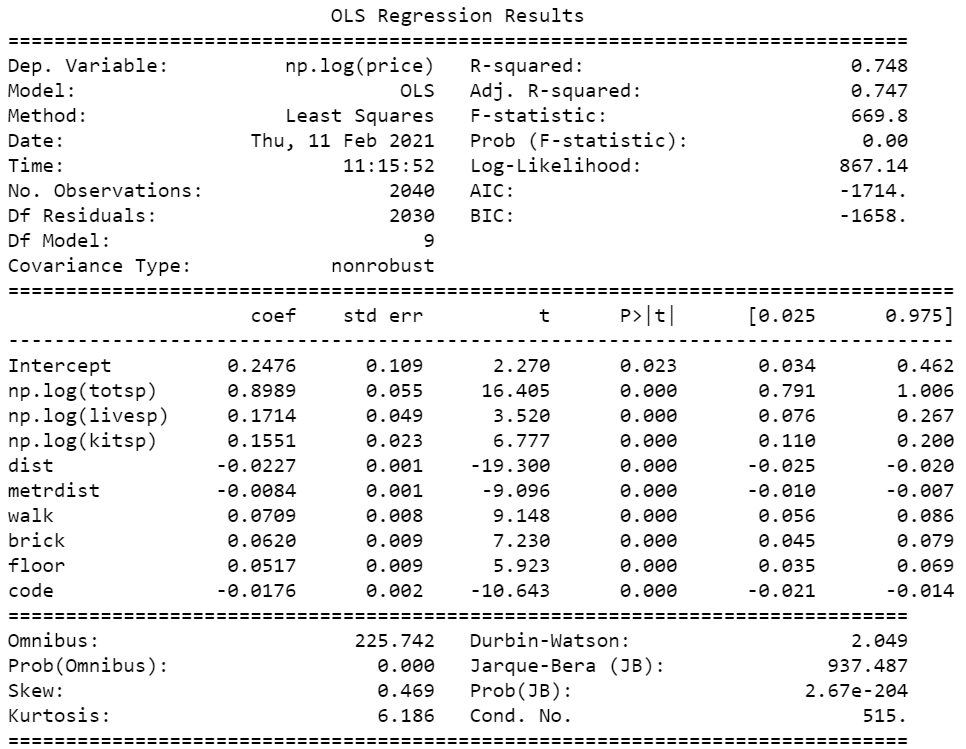
При построении моделей так же важно перекодировать категориальные переменные. В sklearn нам бы пришлось все так же вручную создавать новые n — 1 переменные, где – кол-во категорий. Используя statsmodel достаточно изменить тип столбца на категориальный.
df["code"] = df["code"].astype('category')Построим такую же модель на преобразованных данных.
model_3 = smf.ols('np.log(price) ~ np.log(totsp) + np.log(livesp) + np.log(kitsp) + dist +'\
' metrdist + walk + brick + floor + code', data=df).fit()
print(model_3.summary())
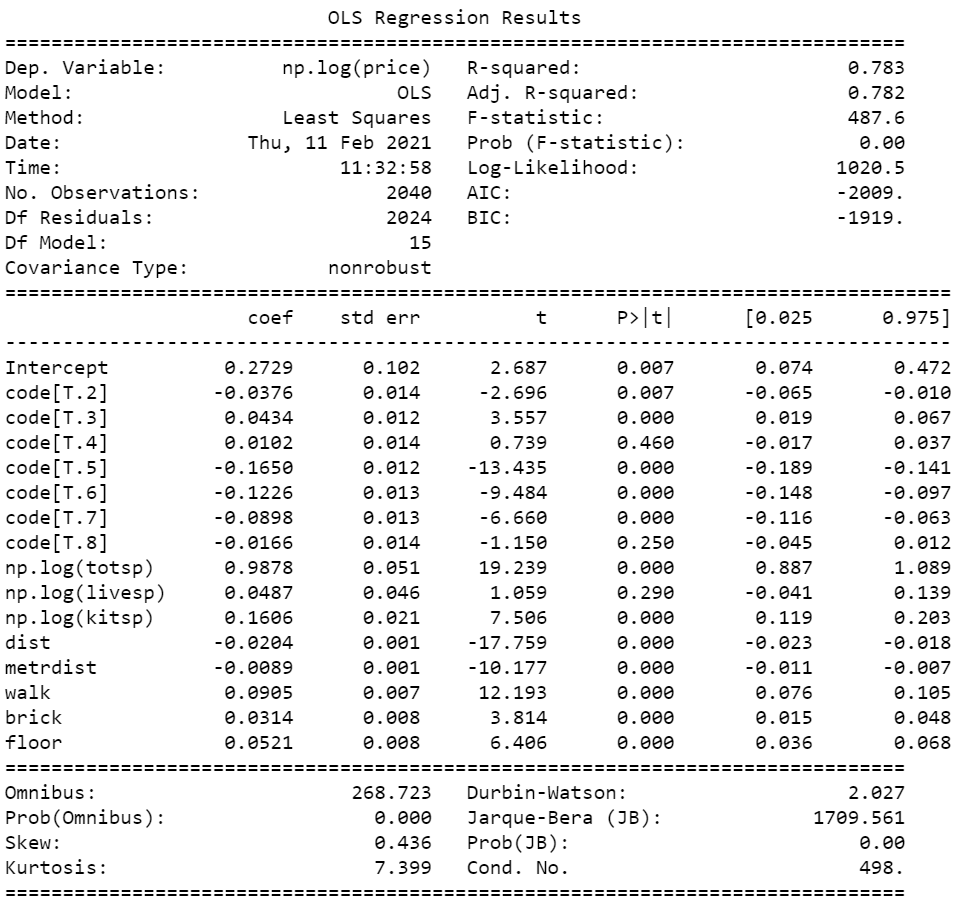
Обратим внимание на достигнутый уровень значимости логарифма признака kitsp в столбце R > |t|. Он больше 0.05 , т.е. мы не можем отклонить гипотезу о незначимости этого признака. Это вполне логично, так как информацию, которую в себе содержит это признак могут уже содержать totsp и livesp. Удалим его. К категориальным признакам данных подход не применим.
Таким образом мы убедились, что для построения модели линейной регрессии, удобно использовать библиотеку statsmodel. Почему в линейных моделях нельзя перекодировать категориальные признаки в n новых, то есть использовать One-hot encoding, обсудим в следующей статье.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
