Время прочтения: 8 мин.
А/В-тестирование – это метод, который используется для сравнения двух версий переменной, например, дизайна сайта при маркетинговом исследовании с целью выявления лучшей версии. Это критически важный метод исследования в Data Science, который часто используется различными организациями при принятии решений с целью оптимизации существующего продукта и максимизации прибыли.
Представлю, что компания, продающая мебель, хочет увеличить число кликов по баннеру «Мебель на заказ». Они значительно изменили дизайн сайта для этой цели. К сожалению, не существует способов предсказать, как именно изменится поведение людей на обновленном сайте по сравнению со старой версией. А/В-тестирование может помочь, например, измерить разницу в конверсии между двумя версиями сайта и сказать, является ли эта разница статистически значимой.
Основные понятия
Прежде чем перейти к проведению А/В-тестирования, введу следующие понятия:
- Нулевая и альтернативная гипотезы
- Уровень значимости (α)
- P-value
- Доверительный интервал
- Статистическая мощность
Нулевая гипотеза в рамках А/В-тестирования – предположение о том, что разницы между версиями сайта А и В в действительности нет, а все наблюдаемые различия обусловлены случайностью. Моя задача в ходе А/В-тестирования – опровергнуть нулевую гипотезу. Альтернативная гипотеза в рамках А/В-тестирования утверждает, что версии сайта А и В различны с точки зрения поведения пользователей.
Уровень значимости – это порог вероятности для определения того, являются ли результаты эксперимента статистически значимыми. Чаще всего уровень значимости устанавливается равным 0,05. Это значит, что моё утверждение о значимости результата будет справедливо на 95%. Чем ниже выбранный уровень значимости, тем ниже риск того, что будет обнаружена разница, вызванная случайностью.
P—value – это вероятность наблюдения данного результата при условии, что нулевая гипотеза верна. Если p-value меньше, чем уровень значимости (α), то отвергается нулевая гипотеза в пользу альтернативной (то есть результаты являются статистически значимыми). Например, при уровне значимости 0,05 p-value должна быть меньше 0,05 для признания результатов эксперимента статистически значимыми.
Доверительный интервал – интервал значений, в котором, с вероятностью (1- α), лежит истинное значение переменной. Доверительный интервал является оценкой возможных значений переменной в зависимости от её стандартного отклонения.
Статистическая мощность – вероятность отклонения нулевой гипотезы в случае, если альтернативная гипотеза верна. Обычно статистическая мощность теста устанавливается равной 0,8. Это значение используется для вычисления размера выборки, необходимой для подтверждения гипотезы с необходимой силой эффекта.
Организация эксперимента
Для проведения А/В-теста требуется разделить всех пользователей на две группы: одна группа будет видеть старый дизайн сайта, а другая – новый. Пользователи распределяются между группами случайным образом. Как правило, группу, которой показывают новый дизайн сайта (В), называют тестовой, а группу, которой показывают старый дизайн (А) – контрольной.
Целевая метрика – CTR, то есть количество кликов на баннер, делённое на количество показов. Буду сравнивать среднее значение метрики CTR для контрольной и тестовой групп. Предположу, что в контрольной группе среднее значение метрики составляет 12%, а в тестовой – 14%.
Если среднее значение метрики в тестовой группе выше, чем в контрольной, то означает ли это, что дизайн сайта В лучше дизайна сайта А? Ответ: нет. Необходимо показать, что результаты А/В-теста статистически значимы. Это означает, что различие в версиях наблюдается не случайно и не обусловлено какой-либо ошибкой. Проверить это можно с помощью статистических тестов.
Не буду заниматься сбором данных в рамках данной публикации. Буду анализировать данные, взятые из датасета с Kaggle. Скачать его можно здесь.
В описании датасета нет информации о том, как именно были собраны данные, но можно предположить, как это было сделано. Перед началом сбора данных рассчитывается размер контрольной и тестовой групп, а также продолжительность эксперимента. Вероятнее всего, размер выборки, необходимой для проведения эксперимента, был рассчитан с помощью калькулятора. Пример такого калькулятора находится здесь. Калькулятор подсчитывает необходимое количество просмотров для каждой версии сайта. В моём случае количество просмотров каждой версии составило 147 239. Для планирования эксперимента это число необходимо поделить на количество пользователей, которое ежедневно будет видеть каждую версию сайта. Предположу, что ежедневный трафик в данном случае составил 10 000 пользователей, это означает, что только 5 000 пользователей могли увидеть каждую версию сайта. Таким образом, количество дней, в течение которых проводился эксперимент, составило 147 239/5 000 ≈ 29 дней.
Реализация на Python
Рассмотрю, как проанализировать результаты А/В-тестирования с помощью Python.
Импортирую библиотеки:
import numpy as np
import pandas as pd
import scipy.stats as stats
import statsmodels.stats.api as sms
import seaborn as sns
from math import ceil
from statsmodels.stats.proportion import proportions_ztest, proportion_confint
Для начала рассчитаю минимальный размер выборки, который нужно взять для наблюдения желаемого эффекта. Допустим, я хочу достигнуть разницы в конверсии 2% за счёт введения нового дизайна сайта. Тогда с учётом изначальной конверсии 12%, статистической мощности 0,8 и уровня значимости 0,05 имею:
effect_size = sms.proportion_effectsize(0.12, 0.14)
required_n = sms.NormalIndPower().solve_power(effect_size, power=0.8, alpha=0.05, ratio=1)
required_n = ceil(required_n)
print(required_n)
Вывод:

Итак, для каждой группы (А или В) необходимо выбрать минимум 4 433 наблюдений.
Импортирую датасет:
df = pd.read_csv('ab_data.csv')
df.head()
Вывод:
Датасет содержит ID пользователей, время посещения, принадлежность к тестовой или контрольной группе, дизайн сайта, который видит пользователь, а также информацию о том, был ли клик на баннер для данного пользователя (1 – клик был, 0 – не был). ID пользователей не уникальны, т.к. некоторые пользователи заходили на сайт несколько раз. Эти пользователи будут искажать результат эксперимента, согласно правилам проведения А/В-тестирования их нужно убрать.
# Пользователи, которые заходили на сайт несколько раз
session_counts = df['user_id'].value_counts(ascending=False)
multi_users = session_counts[session_counts > 1].count()
# Удаление пользователей с несколькими сессиями
users_to_drop = session_counts[session_counts > 1].index
df = df[~df['user_id'].isin(users_to_drop)]
Я должна случайным образом определить 4 433 пользователей, которые видели версию сайта А, и 4 433 пользователей, которые видели версию сайта В.
# Определение выборок для контрольной и тестовой группы
control_sample = df[df['group'] == 'control'].sample(n=4433, random_state=43)
treatment_sample = df[df['group'] == 'treatment'].sample(n=4433, random_state=43)
ab_test = pd.concat([control_sample, treatment_sample], axis=0)
ab_test.reset_index(drop=True, inplace = True)
Далее, определю функции для стандартного отклонения (std_dev) и стандартной ошибки (std_error) на основе ранее импортированных библиотек.
def std_dev(x):
return np.std(x, ddof=0)
def std_error(x):
return stats.sem(x, ddof=0)
Посчитаю значение функций для контрольной и тестовой группы.
conversion_rate = ab_test.groupby('group')['converted'].agg([np.mean, std_dev, std_error])
conversion_rate.columns =['conversion_rate','std_deviation','std_error']
conversion_rate
Вывод:
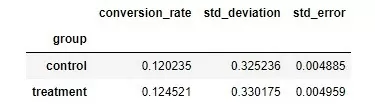
Значения метрик conversion_rate, std_deviation и std_error в контрольной и тестовой группе посчитаны для наглядности. Например, видно, что conversion_rate в тестовой группе несколько выше, чем в контрольной, с примерно одинаковой ошибкой. Однако, как будет показано в дальнейшем, этот результат не является статистически значимым.
Рассчитаю количество «успехов» (т.е. конвертаций показа в клик) для контрольной и тестовой групп, а также общее количество показов.
# Количество показов для контрольной группы
control_results = ab_test[ab_test['group']=='control']['converted']
num_control = control_results.count()
# Количество показов для тестовой группы
treatment_results = ab_test[ab_test['group']=='treatment']['converted']
num_treatment = treatment_results.count()
# «Успехи»
successes = [control_results.sum(), treatment_results.sum()]
# Показы
nobs = [num_control, num_treatment]
Рассчитаю значение p-value, z-статистику и доверительный интервал с помощью статистических функций из модуля statsmodels.stats.proportion.
z_stat, pval = proportions_ztest(successes, nobs = nobs)
(lower_con, lower_treat), (upper_con, upper_treat) = proportion_confint(successes, nobs=nobs)
Вывод:

Как видно, p-value равно 0,538, что больше, чем 0,05 (уровень значимости). Таким образом, нельзя отвергнуть нулевую гипотезу. Это значит, что нет статистически значимого различия между версиями сайта А и В. Наблюдаемая разница в метрике CTR – результат действия случайных факторов.
Кроме того, я посчитала доверительный интервал для контрольной и тестовой групп, куда с 95-процентной вероятностью входит истинное значение конверсии для этих групп.
Если проделать аналогичные расчеты на всем объеме наблюдений (143 345 образцов в каждой группе А и В после удаления дублей), то получу аналогичный результат: p_value равно 0,232, что больше 0,05. Таким образом, нельзя отвергнуть нулевую гипотезу.

Это дополнительно доказывает, что для моих расчетов я имела право взять минимально допустимый объем выборки, равный, как показано выше, 4 433 образцам.
Подведение итогов
В моём случае А/В-тест показал отрицательный результат. Количество конвертаций показов в клик не зависит от версии сайта А или В, которую видит пользователь. Таким образом, можно сделать вывод, что дизайн сайта не влияет на конверсию. Или же, возможно, дизайн сайта имеет влияние, но версии А и В должны отличаться более радикальным образом. Например, нужно не просто изменить цвет обложки сайта, но и кардинально поменять дизайн кнопок и их размещение на подложке. Дальнейшая доработка дизайна сайта и последующие за этим новые А/В-тесты должны производиться при совместном участии продуктового аналитика и UX-дизайнера.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
