Время прочтения: 5 мин.
Используем Numpy
Установим необходимые пакеты:
pip install numpy pandas matplotlibСоздадим случайный набор данных, имеющих нормальное распределение. Надо отметить, что в теории вероятностей нормальное распределение – это весьма распространенное, непрерывное распределение вероятностей, симметричное относительно среднего. Оно показывает, что данные, близкие к среднему, встречаются чаще, чем данные, далекие от среднего. Нормальные распределения используются в статистике для представления случайных величин с действительными значениями. Например, данные роста, артериального давления, IQ подчиняются нормальному распределению.
В приведенном ниже коде создадим случайный набор данных:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# инициализируем параметры для нормального распределения:
# определение среднего
mu = 0.5
# определение стандартного отклонения
sigma = 0.1
# random использует начальное значение в качестве основы
# для генерации случайного числа.
np.random.seed(0)
# определим координаты x
X = np.random.normal(mu, sigma, (546, 1))
# определим координаты y
Y = np.random.normal(mu * 2, sigma * 3, (546, 1))
# строим граф
plt.scatter(X, Y, color = 'r')
plt.show()
Вывод графа:
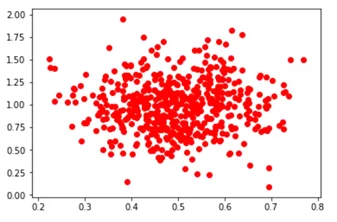
Теперь создадим немного другой набор данных, включающих 3 столбца, которые представляют функцию в наборе данных и еще один 4-й столбец – метки вывода, значения которых меняются в пределах от 0 до 3. Созданный таким способом набор данных можно использовать для обучения, к примеру, классификатора логистической регрессии или классификатора нейронной сети.
import numpy as np
import pandas as pd
import math
import random
import matplotlib.pyplot as plt
# определение столбцов с использованием нормального распределения
# столбец1
point1 = abs(np.random.normal(1, 15, 50))
# столбец2
point2 = abs(np.random.normal(2, 10, 50))
# столбец3
point3 = abs(np.random.normal(3, 4, 50))
# x содержит функции датасета
x = np.c_[point1, point2, point3]
# метки вывода варьируются от 0 до 3
y = [int(np.random.randint(0, 3)) for i in range(50)]
# определяем DataFrame для последующего использования
data = pd.DataFrame()
# определяем столбцы датасета
data['col1'] = point1
data['col2'] = point2
data['col3'] = point3
# построение функций (x) по меткам (y)
plt.subplot(2, 2, 1)
plt.title('col1')
plt.scatter(y, point1, color ='r', label ='col1')
plt.subplot(2, 2, 2)
plt.title('Col2')
plt.scatter(y, point2, color = 'g', label ='col2')
plt.subplot(2, 2, 3)
plt.title('Col3')
plt.scatter(y, point3, color ='b', label ='col3')
# сохраняем граф
plt.savefig('dataset.jpg')
# отображение графа
plt.show()
Результат вывода графа:
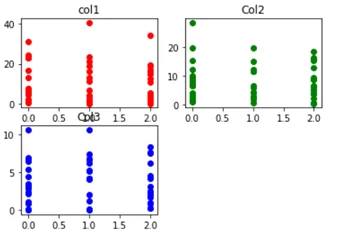
Используем Sklearn
Sklearn имеет генератор образцов наборов данных. Процесс создания датасета несложный и быстрый. Далее приведу примеры того, как это сделать. Импортируем необходимые библиотеки:
from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt
from matplotlib import style
Генерирование изотропных Гауссовских капель для кластеризации с помощью функции make_blobs ()
Датасет подходит для задач линейной классификации с учетом линейно разделяемой природы двоичных объектов.
# Создаем тестовый датасет с использованием make_blobs
from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt
from matplotlib import style
style.use("fivethirtyeight")
X, y = make_blobs(n_samples = 300, centers = 3,
cluster_std = 1, n_features = 2)
plt.scatter(X[:, 0], X[:, 1], s = 40, color = 'b')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
Вывод результата:
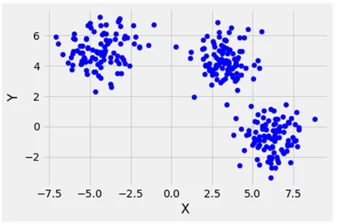
Генерирование датасета для задачи двоичной классификации с помощью функции make_moons ()
Этот тестовый датасет подходит для алгоритмов, изучающих нелинейные границы классов.
# Создаем тестовый датасет с использованием make_moon
from sklearn.datasets import make_moons
from matplotlib import pyplot as plt
from matplotlib import style
X, y = make_moons(n_samples = 500, noise = 0.1)
plt.scatter(X[:, 0], X[:, 1], s = 40, color ='r')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
plt.clf
Вывод результата:
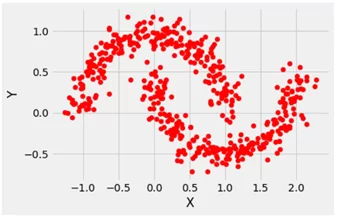
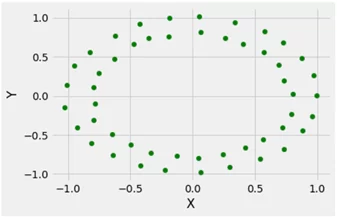
Генерирование датасета для задачи двоичной классификации с помощью функции make_circles ()
Этот датасет подходит для алгоритмов, изучающих сложные нелинейные многообразия.
# Создаем тестовый датасет с использованием make_circles
from sklearn.datasets import make_circles
from matplotlib import pyplot as plt
from matplotlib import style
style.use("fivethirtyeight")
X, y = make_circles(n_samples = 50, noise = 0.02)
plt.scatter(X[:, 0], X[:, 1], s = 40, color ='g')
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
plt.clf()
Вывод:
В приведенных примерах с использованием Numpy и Sklearn показаны способы создания случайных наборов данных. И несмотря на то, что такие датасеты не могут учесть всех особенностей реального набора данных, они хорошо контролируемы, чтобы быть использованными для обучения и исследования сильных и слабых качеств вашей модели.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
