Время прочтения: 5 мин.
Математическое моделирование нашло широкое применение в различных областях науки, в том числе в медицине. Возможность воспроизвести результат, не прибегая к реальным экспериментам, весьма полезна по ряду причин: это быстро, дешево, этично. Я приведу пример построения модели распространения инфекции. Для этого нам потребуется немного математики и небольшой скрипт на python. Для визуализации будем использовать библиотеку matplotlib. Модель будет упрощенная, т.е. мы пропустим ряд параметров, влияющих на распространение болезни. Поэтому нельзя сказать, что реальная инфекция распространяется именно так, как на графиках ниже. Хотя некоторые тенденции все-таки будут прослеживаться.
Будем наблюдать за группой мышей, в которой доля привитых (вакциной против некого патогена) равна vасс_ratio. Допустим нам известно, что патоген распространяется по воздуху не дальше, чем на расстояние distination. И на расстоянии менее или равным distination заражает некоторый процент среди привитых мышек и некоторый процент среди непривитых. Особь продолжает выделять патоген еще некоторое время после заражения – ill_durat, далее она становится безопасной для окружающих.
Импортирую необходимые библиотеки:
import numpy as np
import random
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation
Задаю начальные условия:
population = 100# Количество точек
vacc_ratio = 0.9 # Доля вакцинированных
vacc_infect_prb = 0.05 # Вероятность заражения вакцинированной точки
not_vacc_infect_prb = 0.4 # Вероятность заражения невакцинированной точки
distination = 0.08 # Расстояние для заражения
ill_durat = 12 # Длительность выделения патогена точкой
timer = 100 # Время наблюдений
Одна мышка — это точка на плоскости, имеющая координаты (x, y). Привитых мышек обозначим зеленым цветом, а непривитых — синим. Мышки время от времени перемещаются (меняют свои координаты). Первую точку мы заразим искусственно, и отметим красным цветом.
Создаем Dataframe наблюдений, содержащий идентификатор точки, временную метку, цвет, координаты точки, и время заболевания.
# Задаем координаты, начальное время, ID, цвет (состояние), время заражения
X = pd.Series(np.random.rand(population))
Y= pd.Series(np.random.rand(population))
time = [0.0]*population
id = pd.Series(range(0,population))
color = ['green']*int(population*vacc_ratio)+['blue']*(population-int(population*vacc_ratio))
# Первое заражение
first_infect_id = random.randint(0,population-1)
color[first_infect_id] = 'red'
infect_date = pd.Series([-1]*population)
infect_date[first_infect_id] = 0
# Сохраняем в DateFrame
observ_df = pd.DataFrame({ 'ID': id, 'time':time, 'color': color, 'X': X, 'Y':Y,'infect_date':infect_date })
Далее запустим цикл, который обновляет состояния на каждой итерации (одна итерация — одна единица времени) и сохраняет эти состояния в общей таблице.
for i in range(1, timer):
# Cоединяем таблицу наблюдений саму с собой, чтобы получить все пары точек (сочетание без повторений).
cross_observ = observ_df.merge(observ_df, how='cross',suffixes=('_1', '_2'))
cross_observ = cross_observ[cross_observ['ID_1'] < cross_observ['ID_2']]
# Считаем евклидово расстояние между каждой парой точек и записываем его в столбец destinaton
cross_observ['destinaton']=cross_observ.apply(lambda obs: np.sqrt((obs['X_1'] - obs['X_2']) ** 2 + (obs['Y_1'] - obs['Y_2']) ** 2), axis=1)
# Рассчет новых состояний точек
a = cross_observ.apply(func=change_color, axis=1)
# Обновляем DataFrame observ df в связи с изменением состояний некоторых точек после применения функции change_color
df_new_1 = pd.DataFrame()
df_new_2 = pd.DataFrame()
df_new = pd.DataFrame()
df_new_1[['ID','color','infect_date']] = a[a['color_1']=='red'][['ID_1', 'color_1','infect_date_1']].drop_duplicates()
df_new_2[['ID','color','infect_date']] = a[a['color_2'] == 'red'][['ID_2','color_2','infect_date_2']].drop_duplicates()
df_new[['ID', 'color','infect_date']] = pd.concat([df_new_1, df_new_2],ignore_index=True).drop_duplicates()
observ_df = observ_df.merge(df_new, how='left', on=['ID'], suffixes=('', '_new'))
observ_df['color'] = np.where(pd.notnull(observ_df['color_new']), observ_df['color_new'], observ_df['color'])
observ_df['infect_date'] = np.where(pd.notnull(observ_df['infect_date_new']), observ_df['infect_date_new'], observ_df['infect_date'])
observ_df.drop(['color_new','infect_date_new'], axis=1, inplace=True)
# Добавляем observ_df в общий DataFrame
observ_all = observ_all.append(observ_df)
# Обновляем время и координаты точек
observ_df['time'] = i
if i%5 == 0:
observ_df['X'] = pd.Series(np.random.rand(population))
observ_df['Y'] = pd.Series(np.random.rand(population))
Реализация функции change_color():
#Если 2 точки находятся на расстоянии не более destination
# и только одна из точек помечена красным(заражена),
# и с момента ее заражения прошло не более ill_durat,
# тогда вторая точка окрашивается красным (заражается) с вероятностью
#vacc_infect_prb, если она была привита и с вероятностью not_vacc_infect_prb, если непривита.
def change_color(row):
if row['destinaton'] <= distination and row['color_1']== 'red' and (row['time_1'] - row['infect_date_1']) < ill_durat:
if row['color_2']=='blue':
row['color_2'] = np.random.choice(['blue', 'red'], p=[1 - not_vacc_infect_prb, not_vacc_infect_prb])
if row['color_2']=='red':
row['infect_date_2'] = row['time_1']
if row['color_2'] == 'green':
row['color_2'] = np.random.choice(['green', 'red'], p=[1 - vacc_infect_prb, vacc_infect_prb])
if row['color_2'] == 'red':
row['infect_date_2'] = row['time_1']
if row['destinaton'] <= distination and row['color_2']== 'red' and (row['time_1'] - row['infect_date_2']) < ill_durat:
if row['color_1']=='blue':
row['color_1'] = np.random.choice(['blue', 'red'], p=[1 - not_vacc_infect_prb, not_vacc_infect_prb])
if row['color_1'] == 'red':
row['infect_date_1'] = row['time_1']
if row['color_1'] == 'green':
row['color_1'] = np.random.choice(['green', 'red'], p=[1 - vacc_infect_prb, vacc_infect_prb])
if row['color_1'] == 'red':
row['infect_date_1'] = row['time_1']
return row
Осталось создать анимированные графики и сохранить их в формате gif.
fig, ax = plt.subplots()
x, y = [], []
sc = ax.scatter(x, y)
sc.set_cmap("brg")
plt.xlim(0, 1)
plt.ylim(0, 1)
ttl = ax.text(-0.05, 1.05, "", transform=ax.transAxes, fontsize=14)
def animate(i):
ill_prc = int(observ_all[(observ_all['time']==i) & (observ_all['color']==0.5)]['ID'].count()/population *100)
ttl.set_text('vacc_ratio = {}, time = {}, ill_prc = {}'.format(vacc_ratio, i,ill_prc))
x = list(observ_all[observ_all['time']==i]['X'])
y = list(observ_all[observ_all['time'] == i]['Y'])
colors = list(observ_all[observ_all['time'] == i]['color'])
sc.set_offsets(np.c_[x,y])
sc.set_array(colors)
ani = matplotlib.animation.FuncAnimation(fig, animate,frames=timer-1, interval=1, repeat=True)
# Сохраняем анимацию в виде gif файла:
my_writer=matplotlib.animation.PillowWriter(fps = 8)
ani.save('vacc_ratio='+str(vacc_ratio)+'.gif',writer=my_writer)
Теперь, изменяя параметры vacc_ratio, vacc_infect_prb, not_vacc_infect_prb, distination, ill_durat можно наблюдать за охватом и скоростью распространения инфекции. Изменяя параметр vacc_ratio c 30% до 90%, я построила следующие графики:
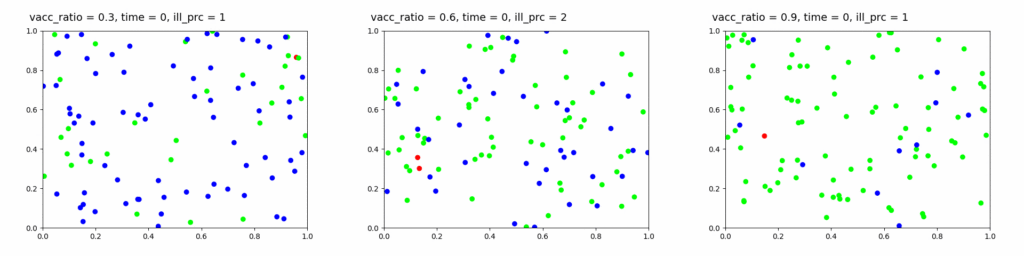
Те же результаты, но в табличном виде (в абсолютных и относительных значениях:
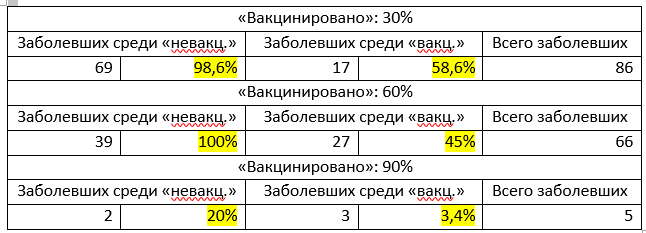
В заключение, я не хотела углубляться в биологию, ведь модель условная и упрощенная, и, вообще, я не биолог. Однако, я могу обратить ваше внимание на бОльшую важность относительных значений перед абсолютными (см. последнюю строку таблицы).
В реальной жизни похожие модели применяются для оценки распространения различных инфекционных заболеваний в мегаполисах. И, конечно, они куда сложнее, и учитывают большее количество параметров. Например, пол и возраст человека, карту города и перемещения людей по этому городу, статус (студент, работающий, школьник детсадовец, безработный), продолжительность инкубационного периода, вирусную нагрузку в зависимости от периода инфекции и т.д. Но даже на такой простой модели как наша, можно заметить эффект, называемый в эпидемиологии, — коллективным иммунитетом.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
