Время прочтения: 3 мин.
Для начала рассмотрим на примере работу метода std() двух библиотек pandas и numpy. Импортируем необходимые для обработки данных библиотеки:
import pandas as pd
import numpy as np
Посмотрим на результат работы для заданного массива чисел:
num_list = [1, 2, 3, 4, 6, 2, 4, 2, 6, 3, 3, 3, 8, 4, 3, 2, 1]
df_num_list = pd.DataFrame(num_list)
print('Стандартное отклонение, используя pandas.std() = {}'.format(df_num_list[0].std()))
print('Стандартное отклонение, используя numpy.std() = {}'.format(np.std(num_list)))

А почему они разные? Давайте разбираться.
Среднеквадратичное отклонение (англ. standard deviation) – показатель рассеивания значений случайной величины относительно её математического ожидания.
Для начала давайте разберёмся с нормальным распределением. На рисунке показан график нормального распределения. По середине проходит нормаль: справа и слева от неё одинаковое количество наблюдений.
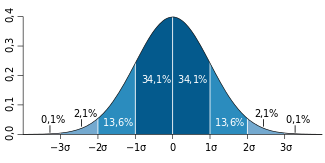
На графике на оси Х отмечены 3 сигмы. Наблюдение «не вылезет» за пределы сигмы с вероятностью 68,2%, за пределы двух сигм – с вероятностью 95,4%, за пределы трёх сигм – с вероятностью 99,7%. Функции, рассмотренные в начале статьи, вычисляют значение, которое будет вычитаться/добавляться к среднему значению, чтобы получить представление о разбросе/диапазоне значений.
А теперь про вычисление стандартного отклонения с математической точки зрения:
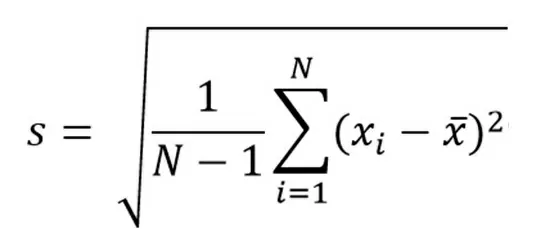
Под знаком суммы вычисляется квадрат разности между средним значением и значением элемента. Дальше всё это суммируется и делится на количество элементов уменьшенное на единицу. В самом конце берется квадратный корень из заданного выражения.
Давайте пошагово проделаем этот алгоритм в Python. Найдем среднее значение с помощью метода mean() библиотеки numpy:
overall_mean = np.mean(num_list)Вычислим количество элементов с помощью функции len:
list_count = len(num_list)В цикле будем проходить по каждому элементу, вычислять квадрат разницы и печатать корень из частного:
sum_of_nums = 0
for num in num_list:
sum_of_nums += (num - overall_mean) ** 2
print((sum_of_nums/(list_count - 1)) ** 0.5)
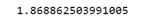
Дело в том, что внутри этих методов происходит деление на разные числа: в библиотеке pandas из N (количества элементов) вычитается единица, а в библиотеке numpy не вычитается ничего (происходит деление на N). Таким образом в первом случае вычисляется стандартное отклонение на основании несмещённой оценки дисперсии, а во втором случае на основании смещённой оценки дисперсии (вычисляется выборочное среднее). В методе std() библиотеки pandas есть параметр ddof, который позволяет задать число для вычета его из N. Зададим единицу и сравним работу методов:
num_list = [1, 2, 3, 4, 6, 2, 4, 2, 6, 3, 3, 3, 8, 4, 3, 2, 1]
df_num_list = pd.DataFrame(num_list)
print('Стандартное отклонение, используя pandas.std() = {}'.format(df_num_list[0].std()))
print('Стандартное отклонение, используя numpy.std() = {}'.format(np.std(num_list, ddof=1)))

Бинго! Всё совпало. Поэтому всегда читайте документацию по работе методов перед их использованием.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
