Время прочтения: 7 мин.
И снова всем привет! Если вас заинтересовала моя недавняя статья «Простая генерация синтетических данных на Python», устраивайтесь поудобнее, заваривайте чай и мы продолжим разбирать эту тему.
В предыдущей статье я показывал, как с помощью готовых библиотек выкрутиться из ситуации, когда необходимо сгенерировать данные в условиях нехватки времени/недостаточности знаний и получить приемлемый результат, с которым вполне можно работать.
Теперь мы рассмотрим ситуацию, когда нас не сковывают два вышеописанных обстоятельства. Зато в распоряжении мы имеем машину со средним железом, не способным на особые подвиги — а точность генерации повысить хочется.
Как я и говорил ранее, ключевым фактором качественного синтеза данных в задачах машинного обучения является то, что на синтетическом наборе данных модель с определенными параметрами будет вести себя так же, как и на реальных данных.
Более гибко и точно процесс генерации позволяет провести байесовская сеть.
Краткий ликбез: понятие байесовской сети неразрывно связано со старой доброй теоремой Байеса. Да-да, той самой, про вероятности взаимозависимых событий:
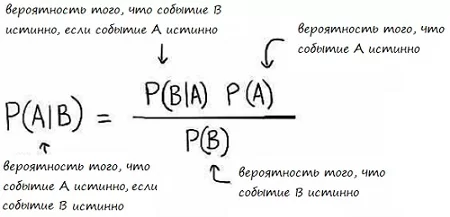
Байесовская сеть – это графическое представление взаимосвязей переменных (событий, факторов) и отношений между ними, основанное на апостериорных вероятностях. Представлен в виде ориентированного ацикличного графа, ребрами которого является отношение между переменными в виде апостериорных вероятностей.
Для лучшего понимания рассмотрим пример из Википедии про мокрый газон. Допустим, есть у нас газон (GRASS WET), который по каким-то причинам может стать мокрым. Пусть будут две такие причины – дождь (RAIN) и срабатывание садовой поливалки (SPINKLER). Также допустим, что поливалка не включится, если на улице в данный момент идет дождь. Данный пример хорошо подходит для иллюстрации Байесовской сети, что мы и сделаем:
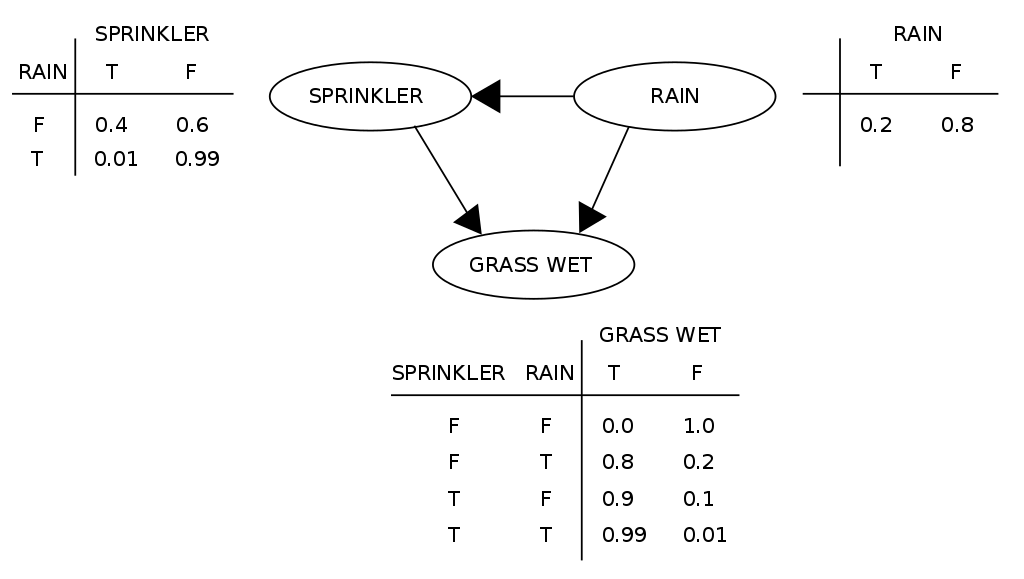
Описанные выше события можно представить в виде трех переменных, которые принимают значения true и false. Вероятности принятия переменными SPINKLER и GRASS WET тех или иных значений являются апостериорными и как раз описываются формулой Байеса. Общая совместная вероятность модели может быть описана как:
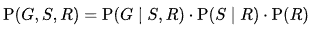
На практике такая модель позволяет как определить вероятность увлажнения газона, если прошел дождь, либо если сработала поливалка, так и пойти от обратного – например, подсчитать вероятность того, что прошел дождь, если известно, что газон мокрый.
Точек приложения у байесовских сетей очень много – например, моделирование в тех или иных областях, предсказания болезней на основе симптоматики, фильтрация спама и прочие задачи. Этот подход можно применить на практике и в генерации данных – байесовская сеть строится на данных, поданных на вход, в результате чего будут подсвечены связи между значениями признаков. Это позволяет построить условные распределения между признаками, а, значит, у нас есть возможность сделать генерацию данных на их основе.
Если у Вас есть желание подробнее ознакомиться с этой темой и всеми её нюансами – прикрепляю ссылку на научную статью.
А мы тем временем перейдем от теории к практике. В качестве данных будем использовать уже хорошо знакомый нам набор данных о клиентах банка, взятый из Интернета:
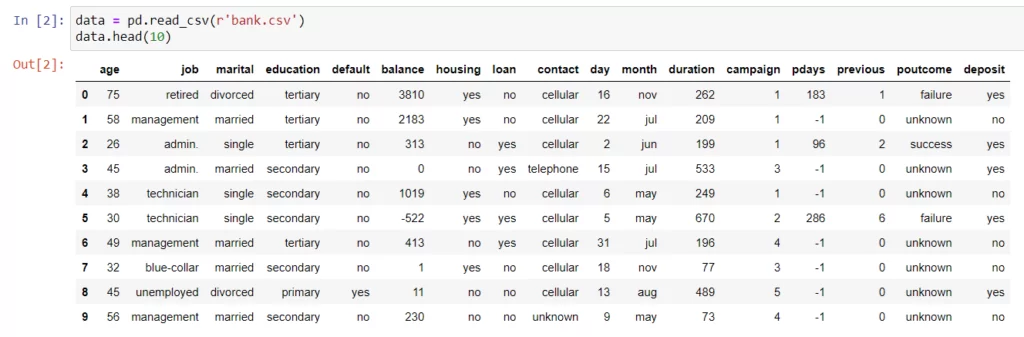
Чтобы использовать Байесовскую сеть как генератор синтетических данных, сначала необходимо предобработать данные:
- Дискретизировать непрерывные числовые величины по бинам.
Пример для понимания: значение непрерывной переменной в диапазоне, скажем, от -10 до 10 мы разобьем на 5 бинов (равных частей). В описанном случае один бин будет включать в себя 4 значения (так как мы интервал в 20 значений разбиваем на 5 частей), после чего каждое исходное значение будет заменено номером бина, в который оно попало. Непрерывный признак станет категориальным (будет принимать малое число целочисленных значений).
Для наглядности привожу иллюстрацию:
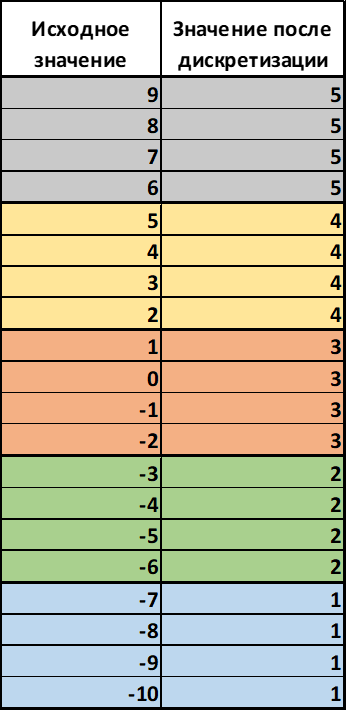
В нашем случае дискретизацию можно произвести следующим образом:
from sklearn.preprocessing import KBinsDiscretizer
est = KBinsDiscretizer(n_bins=5, encode='ordinal', strategy='quantile')
data_discrete = est.fit_transform(data.values[:,[0,5,9,11,12,13,14]])
data[['age','balance', 'day', 'duration', 'campaign', 'pdays', 'previous']] = data_discrete
data.loc[:,:] = data.loc[:,:].astype('int')
2. Закодировать категориальные признаки в числа. Обычный Label Encoder здесь вполне подойдёт.
from sklearn.preprocessing import LabelEncoder
data[['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome', 'deposit']] = data['job', 'marital', 'education', 'default', 'housing', 'loan', 'contact', 'month', 'poutcome', 'deposit']].apply(LabelEncoder().fit_transform)
В результате предобработки все признаки в нашем датасете становятся целочисленными и категориальными:
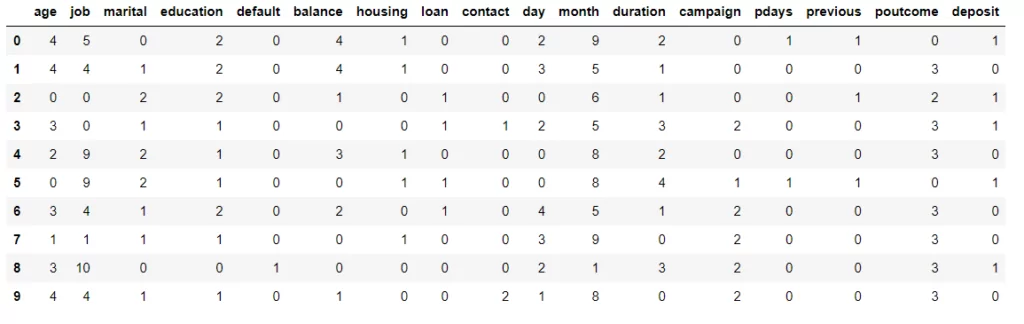
Здесь возникает логичный вопрос — если исходные данные перед построением Байесовской сети изменяются до такого вида, и, соответственно, синтезируемые данные будут иметь аналогичный вид, то как нам восстановить значения признаков?
- В случае кодирования текстовых категориальных признаков все просто — сохраняем Label Encoder для каждого признака, скажем, в словарь, ключом которого будет название признака, а значением — сами энкодеры. После этого через цикл/df.аpply производим inverse_transform(), и признаки в новых данных примут прежний вид.
- В случае дискретизации, к сожалению, не всё так просто. Тот же KBinsDiscretizer тоже имеет метод inverse_transform(), однако он восстанавливает значения как среднее между максимальным и минимальным значением бина с конкретным номером. Точность восстановления можно повысить, наращивая количество бинов. Но не советую с этим усердствовать — будет расти количество потребляемых ресурсов, да и слишком большим количеством бинов можно нивелировать пользу от преобразования.
Так, с подготовкой данных разобрались. Теперь перейдем к построению байесовской сети. На языке Python это можно сделать с помощью библиотеки PgmPy. В ней реализован алгоритм Hill Climb Search (поиск глобального максимума), строящий сеть, максимально соответствующую входным данным, путем максимизации скоринговой функции. В данной реализации на выбор доступно 3 скоринговых функции: K2, Bic и BDeu. Для каждого конкретного случая лучшую скоринговую функцию можно подбирать эмпирическим путем — тем более алгоритм работает не так уж и долго, если, конечно, на компьютере стоит что-то лучше Intel Celeron.
Ссылка на теорию.
Ниже приведен код использования алгоритма HillClimbSearch для построения байесовской сети:
from pgmpy.estimators import HillClimbSearch
from pgmpy.estimators import BDeuScore, K2Score, BicScore
hc_BicScore = HillClimbSearch(data, scoring_method=K2Score(data))
best_model_BicScore = hc_BicScore.estimate()
Также, с помощью библиотеки networkx построенную сеть можно визуализировать и изучить.
import networkx as nx
G_K2 = nx.DiGraph()
G_K2.add_edges_from(best_model_K2.edges())
pos = nx.layout.circular_layout(G_K2)
nx.draw(G_K2, pos, with_labels=True,font_weight='bold')
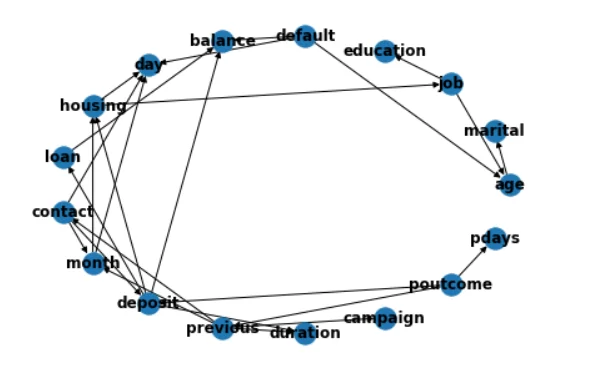
Теперь после построения сети её можно использовать для генерации новых данных. Сделать это можно следующим образом:
from pgmpy.models import BayesianModel
from pgmpy.sampling import BayesianModelSampling
def sampling (bn: DAG, data: pd.DataFrame, n: int = 100):
bn_new = BayesianModel(bn.edges())
bn_new.fit(data)
sampler = BayesianModelSampling(bn_new)
sample = sampler.forward_sample(size=n, return_type='dataframe')
return sample
Применение этой функции будет выглядеть так:
sample_K2 = sampling(best_model_K2, data, 600)
Sample_K2 — это новые данные, синтезированные байесовской сетью. Сравним их с реальными данные тем же методом, что и в прошлой статье — путем построения сравнительных гистограмм.
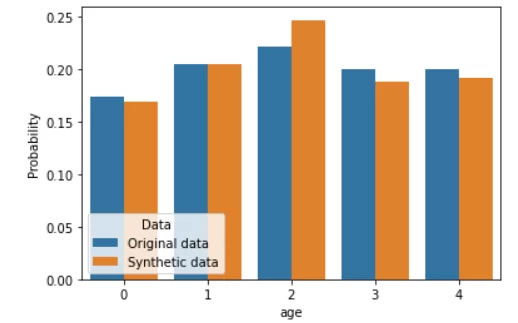
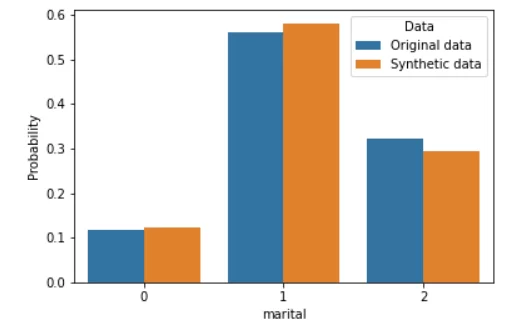
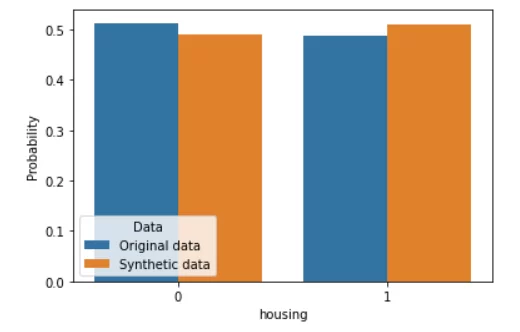
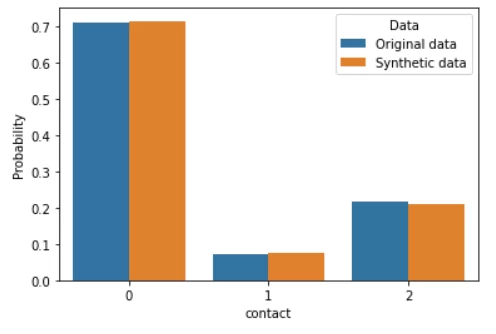
По-моему, выглядит неплохо. В отличие от модели GaussianCopula из библиотеки SDV, при использовании байесовских сетей отсутствует необходимость эмпирически подбирать распределения для каждого признака и надеяться на то, что алгоритм правильно их сформирует. Также, если сравнить гистограммы с таковыми из прошлой статьи, можно убедиться, что генерация данных происходит гораздо точнее. Нагрузка на вычислительные мощности, конечно, выросла, но всё еще остается невысокой.
Из спорных моментов могу указать:
- Как было сказано ранее, необходимо привести данные к исходному виду. В случае дискретизации вероятна потеря точности непрерывных численных значений.
- Генеративно-состязательные сети, пусть для них требуется хорошее железо и большой набор данных, при должном погружении в матчасть и настройке гиперпараметров способны добиться еще большей точности в генерации данных.
- В отличие от модели GaussianCopula из библиотеки SDV, с этой моделью необходимо гораздо большее погружение в матчасть и понимание того, что мы делаем.
На этом всё. Желаю успехов!

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
