Выявление неявных связей при анализе графов или как увидеть незримое

Время прочтения: 8 мин.

Неявные связи в графах. Что это и как с ними работать, разберу на примерах.

Для начала немного теории. Граф — множество узлов, объединенных множеством ребер. С узлами все понятно, взяли города России, клиентов банка или компьютеры в сети, и получили множество объектов, которые и будут узлами для графа. Что же с ребрами? На первый взгляд все просто: города соединены дорогами, клиенты совершают переводы денежных средств, а компьютеры постоянно обмениваются информацией. Все, что было перечислено, относится к явным типам связей. Существует факт взаимосвязи между объектами: если дороги нет, то ребро между узлами отсутствует. Что же относится к неявным связям? Неявные связи сложнее, они могут зависеть от явных связей или же быть самостоятельными. Например, возьмем двух людей, которые работают на абсолютно разных работах, живут в разных концах города. На первый взгляд, они не имеют ничего общего, но при этом они оба по выходным приходят на матч любимой команды – это и есть неявная связь.

Теперь перейдем к практическому примеру. Есть 2 файла:

1. Данные о мошенниках, их номерах телефонов, а также периоды их активности;
2. Данные о клиентах и номерах телефонов с периодами активности.

Данные с номерами телефонов сложно найти в открытом доступе, придется сгенерировать их самостоятельно. Код для генерации необходимых данных расположен по ссылке.

Следующим этапом будет создание графа.  Для этой задачи понадобятся следующие python-библиотеки:

• Pandas – для работы с файлами;
• NetworkX – для создания графа связей, его визуализации;
• Matplotlib и Numpy – нужны для настройки визуализации графа;
• Datetime – для операций над временными данными.

Перед созданием графа взглянем на данные, с которыми нам предстоит работать.

Описание данных:

• index – id клиента / мошенника;
• numbers – номер телефона;

• Date_start – начало периода активности;
• Date_end – окончание периода активности.

Описание загрузки данных и создание графа опущу (ссылка на полный код).

Для визуализации графа буду использовать раскладку графа методом Фрухтермана-Рейнгольда. Данный метод относится к семейству силовых алгоритмов, подробнее о нем можно прочесть в посте по ссылке.

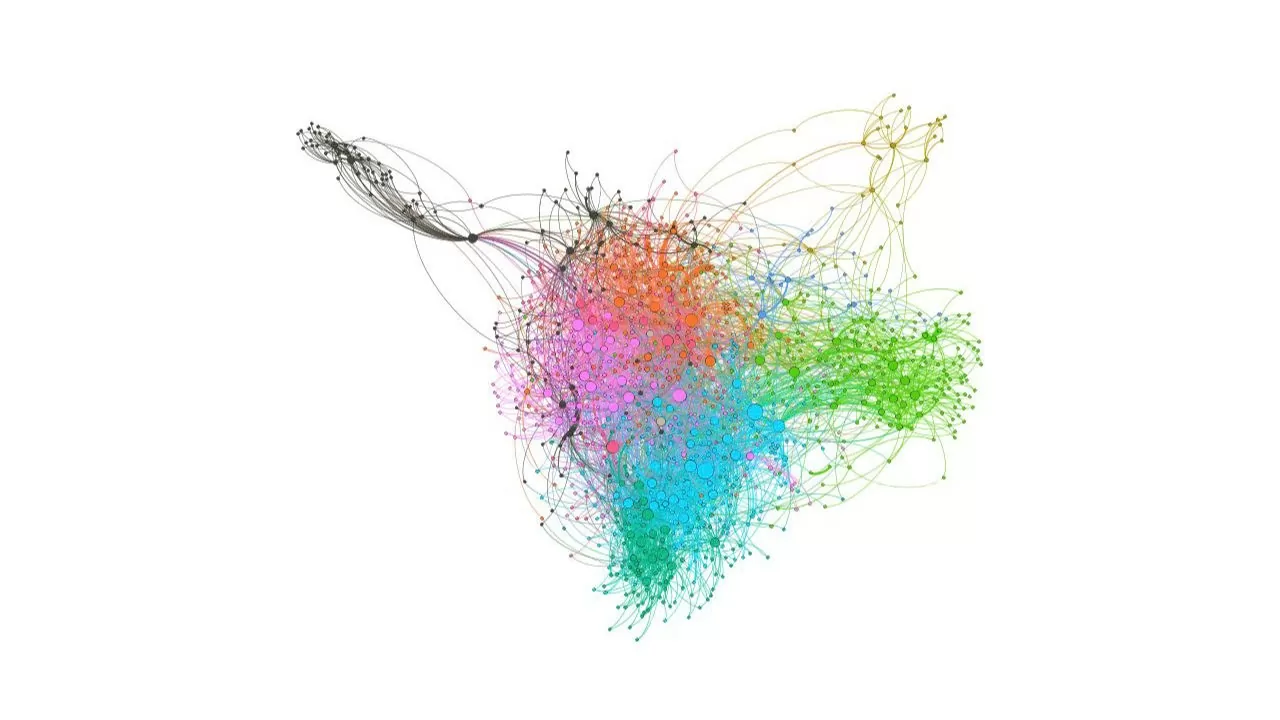
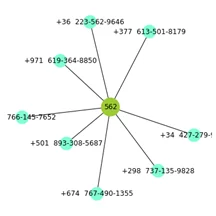
Узлы клиентов – зеленые, узлы телефонов – бирюзовые. Также на узлы наложены аргументы с периодами использования клиентом номера телефона.

На данном этапе граф отображает связь между клиентами и их номерами телефонов. Более наглядно будет выглядеть кейсовое представление, для этого нам понадобится создать датафрейм с подграфами из нашего графа.

# Создаем список подграфов
sub_cc = [graph.subgraph(sub).copy() for sub in nx.connected_components(graph)]

print(f"В нашем графе содержится {len(sub_cc)} подграфа")

# Создаем DataFrame с подграфами и их размерами,
# сортируем так чтобы самый большой подграф - 1
sub_cc = pd.DataFrame().from_dict({ sub: len(sub) for sub in sub_cc},
                                    orient='index',
                                    columns=['len_sub'])\
                        .sort_values('len_sub', ascending=False)\
                        .reset_index()

Для удобства добавим поле с количеством узлов в подграфе и отсортируем таким образом, чтобы подграф с наибольшим количеством узлов был первым, а следующие подграфы следовали по убыванию.

Подграф позволяет более точно анализировать данные на графе. Это очень удобно, если уже есть какие-либо представления.

Следующим этапом будет добавление узлов мошенников и сопоставление периодов использования номеров телефонов. Связь будет устанавливаться только тогда, когда происходит наложение периодов использования номерами телефонов друг на друга.

#   Проверяем условие пересечения периодов   
    if (date_start <= date_start_f <= date_end) or\
                          (date_start <= date_end_f <= date_end):
        
        graph.add_edge(id_ph, int(fr), weight=1.5, size=1000)

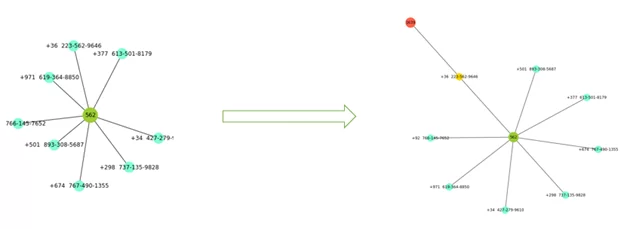
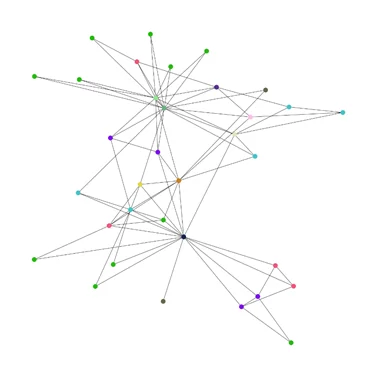
После добавления новых связей граф стал выглядеть немного иначе. Появились узлы мошенников, а телефоны, через которые пролегает связь и периоды пользования совпадают, окрасились в желтый.

Для большей наглядности обратим внимание на подграф, который демонстрировали на первом этапе.

Далее я рассмотрю аналогичные методы выявления связей.

Для выявления неявных связей в графе можно использовать различные методы анализа данных, такие как алгоритмы кластеризации, анализ сходства и различия, анализ сетевых свойств и т.д.

Рассмотрю алгоритм кластеризации. Он может помочь выделить группы вершин, которые имеют схожие свойства или взаимодействуют между собой чаще, чем с другими вершинами, вследствие чего вероятность возникновения связи между узлами одного кластера гораздо выше.

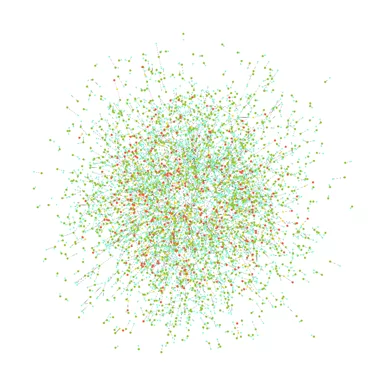
Разберу кластеризацию в networkx на примере, для этого создам граф с помощью метода karate_club_graph(). Метод создает граф социальных связей между людьми в клубе, который хорошо подходит для демонстрации нашего примера.

Так выглядит созданный граф.

Теперь перейду к кластеризации. Для начала вспомним, что это метод машинного обучения для группировки объектов на основе их схожести. В примере я использую его для определения групп людей с похожими характеристиками, что позволяет выявлять неявные связи между ними, так как пользователи в одном кластере могут не быть связаны друг с другом.

Далее я рассмотрю подробнее, как работает кластеризация в NetworkX.

В NetworkX кластеризация проводится с помощью агломеративного алгоритма[1]разбивания графа на отдельные узлы, которые затем объединяются в группы, если имеют высокую степень схожести. Процесс продолжается, пока все узлы не будут объединены в кластеры. Метрика сходства может быть выбрана на основе различных параметров, таких как косинусное или евклидовое расстояние. Для кластеризации в NetworkX существует метод clustering() , который принимает на входе граф и узел и возвращает кластер, к которому принадлежит узел.

for node in G.nodes:
	cl=nx.clustering(G, node)
	if cl not in clusters:
		color, color_list = get_color(color_list)
		clusters[cl] =  {‘nodes’:[node], ‘color’: color}
	else:
		clusters[cl][‘nodes’].append(node)

Для каждого узла из графа вызываю функцию clustering для получения кластера узла, а также присваиваем каждому кластеру свой уникальный цвет с помощью реализованной функции get_color().

def get_color(color_list):
	color = “#”+’’.join([choice(‘0123456789ABCDEF’) for j in range(6)])
	while color in color_list:
		color = “#”+’’.join([choice(‘0123456789ABCDEF’) for j in range(6)])

	return color, color_list

После чего получаю словарь, где в качестве ключа используется кластер, а в качестве значения словарь со списком узлов этого кластера и цветом.

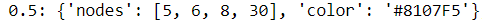
Далее каждому узлу присваиваем цвет в соответствии с цветом кластера, к которому он относится.

И получаем граф, где цвет узла отражает кластер, к которому он относится.

Как можно заметить, узлы зеленого кластера расположились по краям, и большая их часть связана через общее колено (узел, на который опирается одно из ребер). Также можно заметить, что у узлов зеленого кластера по 2 ребра.

Кластеризация может помочь в решении следующих задач:

1. Определение структуры графа: позволяет выявить основные компоненты, такие как вершины и ребра, и определить, как они связаны между собой.

2. Анализ связей между вершинами: могут использоваться для анализа связей между различными вершинами в графе. Например, можно определить, какие вершины связаны друг с другом и какие являются наиболее важными.

В целом, кластеризация является мощным инструментом для анализа и обработки графов, который может помочь в различных задачах, связанных с анализом данных.

Итак, в этом посте я реализовал алгоритм выявления связей между мошенником и клиентом на основе пересечения временных атрибутов, а также разобрал алгоритм кластеризации из библиотеки netwokx. В итоге была найдена связь с мошенником.

В заключение хотелось бы сказать, что данный алгоритм лишь простой пример выявления связей. В нем я разобрал лишь фактор пересечения дат. Необходимо понимать, что графовая аналитика — это полноценный инструмент для анализа, а не средство визуализации. Желаю удачи в покорении вершин Graph Mining!

[1] Агломеративная кластеризация (agglomerative clustering) — это один из методов кластеризации, который начинается с разбиения всех объектов на отдельные кластеры и затем объединяет соседние кластеры, пока не останется только один кластер. Агломеративная кластеризация используется для анализа больших объемов данных и может быть полезна для выявления групп похожих объектов. Она также может быть использована для определения границ кластеров и определения их количества.