Время прочтения: 7 мин.
Мейнстримом последних лет в сфере DS/ML является NLP, в особенности, перспективы использования нейронных сетей, построенных на архитектуре трансформеров. Они используются в том числе в системах голосовых помощников, а голосовые помощники прочно входят в нашу жизнь. Тем не менее, важной составляющей успеха голосовых помощников является то, что они «голосовые», то есть, обращение к ним осуществляется посредством голоса, что значит — аудио. Часто работа с аудиосигналом производится посредством анализа как звука, так и изображения спектрограммы, но в данной статье будут рассмотрены способы представления именно аудио как совокупности различных признаков. Для работы используются библиотеки Python librosa и matplotlib. В качестве основного исходного аудиофайла будет использоваться мелодия открытия обычного сундука из игры The Legend of Zelda: Breath of the Wild в формате wav длительностью ~1 секунда. Информация, представленная в статье, может быть применена в областях speech-to-text, классификации звуков и других направлениях анализа аудио.
Импорт библиотек и загрузка файла:
import librosa
import librosa.display
import matplotlib.pyplot as plt
y, sr = librosa.load(file)
В данном случае, «y» будет массивом чисел, содержащим в себе сам аудиофайл в числовом виде, а «sr» — sample rate, то есть, частотой дискретизации аудио.
Имея эти данные уже можно представить аудио как временной ряд, где по оси Y будет амплитуда сигнала. Следует отметить, что, по умолчанию, librosa.load() считывает файл в моно-режиме. Далее представлен код для отрисовки необходимых представлений:
fig, ax = plt.subplots(nrows=1, sharex=True, sharey=True)
librosa.display.waveplot(y, sr=sr, ax=ax)
ax.set(title='Monophonic')
ax.label_outer()
plt.show()
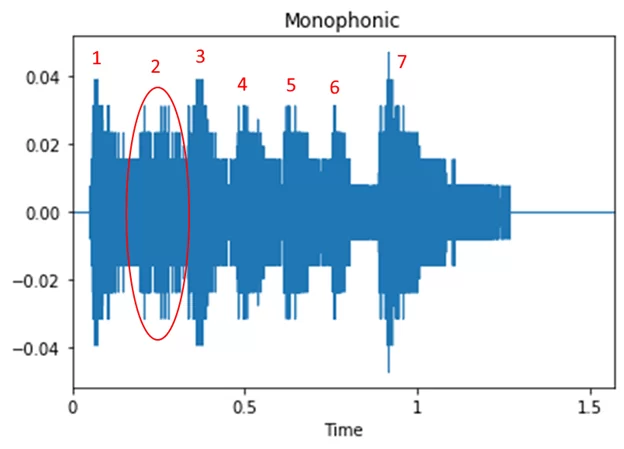
На рисунке 1 можно заметить «бугорки». Если прослушать исходный файл, то станет очевидно, что количество «бугорков» соответствует количеству нот в мелодии (семь), хотя вторая нота «смазанная», что заметно на графике. При этом, акцентированные ноты, а именно: первая, третья и седьмая, звучат резче, громче и это отражено на графике большей амплитудой сигнала.
Теперь же можно посмотреть на более интересное представление аудио. Далее приведён его код:
S = np.abs(librosa.stft(y))
fig, ax = plt.subplots()
img = librosa.display.specshow(librosa.amplitude_to_db(S,
ref=np.max),
y_axis='log', x_axis='time', ax=ax)
ax.set_title('Power spectrogram')
fig.colorbar(img, ax=ax, format="%+2.0f dB")
plt.show()
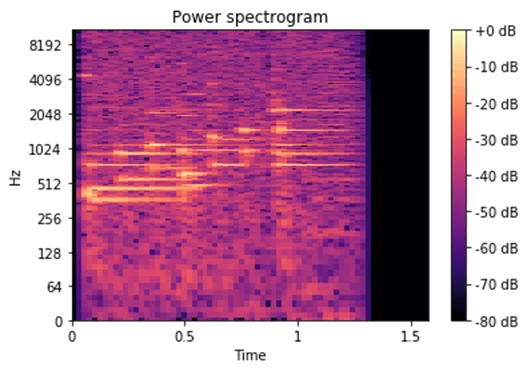
Немного теории для понимания того, что показывает изображенная на рисунке 2 спектрограмма.
Преобразование Фурье разлагает функцию времени (сигнал) на составляющие частоты. Точно так же, как музыкальный аккорд может быть выражен громкостью и частотами составляющих его нот, преобразование Фурье, применённое к функции, отображает амплитуду каждой частоты, присутствующей в базовой функции (сигнале). Именно это мы и видим на рисунке 2. На нём три шкалы – время к частоте, что интуитивно понятно, и дополнительная шкала децибел, показывающая плотность, мощность сигнала на определённой частоте в определённый промежуток времени. Существует альтернативное трёхмерное представление, которое может помочь понять спектрограммы. Оно представлено на рисунке 3:

Так, если сложить все «срезы» трёхмерного представления и «насыщенность» областей отразить цветом, то получится цветное двухмерное представление как на рисунке 2.
Подытожим вышенаписанное: спектрограмма, полученная применением преобразования Фурье к аудиосигналу позволяет «увидеть» как насыщены определённые частоты в аудиосигнале.
Наиболее наглядным, по мнению автора, является сравнение спектрограмм записи классической музыки с лёгким звучанием и какого-нибудь «тяжёлого» жанра с большой плотностью и насыщенностью звука. Пусть, в данном случае, это будут «Чайковский – Танец феи драже» (рисунок 4) и «Megadeth – Symphony of Destruction» (рисунок 5).
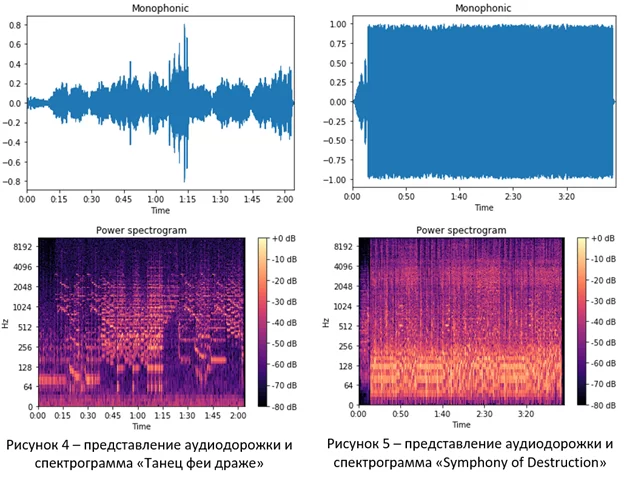
На изображениях аудиодорожек в данном случае видно, что классика и метал сильно отличаются, как минимум, в части громкости: классика может быть тихой и громкой — отчётливо видны места затишья и громких моментов, метал же почти всю композицию звучит только громко.
Спектрограммы же показывают, что в «Танце феи драже» много высоких нот, низких довольно мало – их частоты слабее заполнены, и композиция выстроена сложнее стандартных «куплет-припев». «Symphony of Destruction» же, напротив, практически равномерно заполняет все частоты, ударные и бас-гитара «раскаляют» низкие частоты спектрограммы, композиция содержит много повторяющихся частей.
Теперь, вооружившись знаниями выше, перейдём к разбору, вероятно, наиболее популярного представления аудио в machine learning – мел-кепстральным коэффициентам.
Здесь графики внесут мало понимания, поэтому, сразу приступим к теории:
Если несколько грубо обобщить, то можно прийти к определению, что нота – это колебание определённой частоты, так, Ля первой октавы – это колебания 440 Гц. Однако, человек воспринимает звук неидеально, восприятие высоты звука зависит не только от частоты колебаний, но и от уровня громкости звука и его тембра. Именно для анализа аудио, учитывающего особенности человеческого слуха, была введена психофизическая единица высоты звука – мел. Факт из Википедии: «Звуковые колебания частотой 1000 Гц при эффективном звуковом давлении 2⋅10−3 Па (то есть при уровне громкости 40 фон), воздействующие спереди на наблюдателя с нормальным слухом, вызывают у него восприятие высоты звука, оцениваемое по определению в 1000 мел. Звук частоты 20 Гц при уровне громкости 40 фон обладает по определению нулевой высотой (0 мел). Зависимость нелинейна, особенно при низких частотах (для «низких» звуков).» На рисунке 6 изображена шкала мел к частоте:
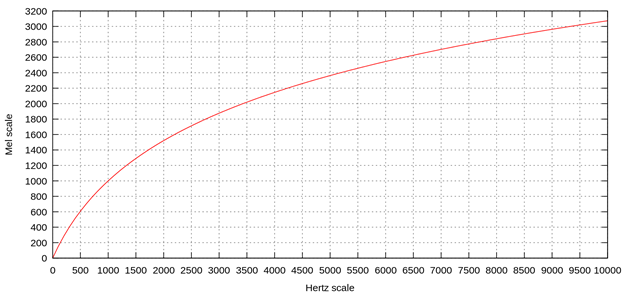
Таким образом, для того чтобы получить спектрограмму, которая будет отражать то, как именно человек воспринимает звучание, необходимо произвести некоторые преобразования, чтобы получить мел-кепстральные коэффициенты. Также, следует отметить, что «некоторые преобразования» устроены таким образом, что большая детализация признаков обеспечивается в области низких частот – наиболее используемых человеком. Ведь, человеческое ухо, в среднем, слышит в диапазоне 20-20000 Гц, при этом (приведём ещё один факт из Википедии): «Голос типичного взрослого мужчины имеет фундаментальную частоту (нижнюю) от 85 до 155 Гц, типичной взрослой женщины от 165 до 255 Гц.». Остальные же составляющие голоса – обертоны. Примерно так же обстоит дело и с музыкальными инструментами.
Подытожим вышенаписанное: мел-кепстральные коэффициенты позволяют нам представить аудио в виде, наиболее близком к восприятию звука человеком.
С помощью библиотеки librosa можно получить данные в нужном виде простым вызовом функции mfcc(). Код вызова функции вместе с отрисовкой результата приведён ниже, а результат выполнения кода представлен на рисунке 7.
mfccs = librosa.feature.mfcc(y=y, sr=sr)
fig, ax = plt.subplots()
img = librosa.display.specshow(mfccs, x_axis='time', ax=ax)
fig.colorbar(img, ax=ax)
ax.set(title='MFCC')
plt.show()
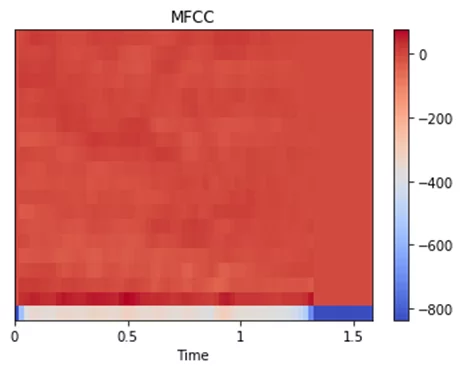
К сожалению, приведённая на рисунке 7 визуализация, по мнению автора, не так наглядна и информативна, как спектрограммы, но ниже также представлены визуализации для «Танца феи драже» (рисунок 8) и «Symphony of Destruction» (рисунок 9):
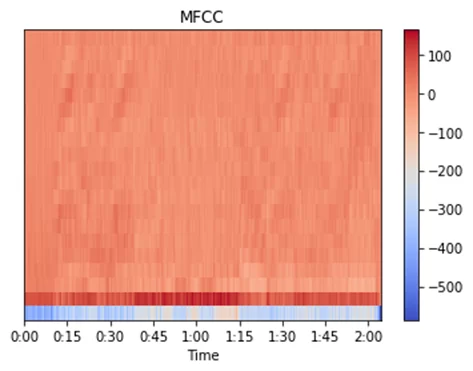
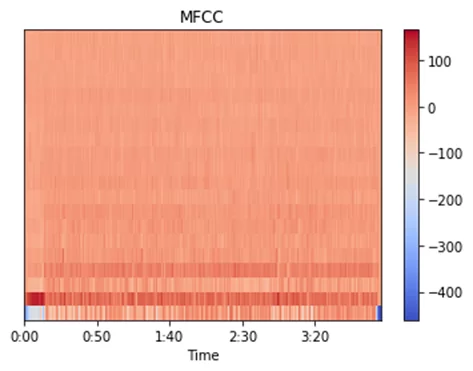
Таким образом, в статье были рассмотрены наиболее часто используемые способы представления аудио в области ML и анализа аудио как такового. Также, проведено наглядное сравнение спектрограмм двух разных музыкальных произведений с целью демонстрации отличий в их наборе признаков. Далее приведены использованные для статьи материалы, которые рекомендуются для более глубокого погружения в тему:
How to apply machine learning and deep learning methods to audio analysis
Audio Deep Learning Made Simple (Part 1): State-of-the-Art TechniquesAudio Deep Learning Made Simple (Part 2): Why Mel Spectrograms perform better

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
