Время прочтения: 6 мин.
Давайте представим, что для работы над задачей классификации вы уже сформировали набор гипотез и определились с признаками. А уже через час необходимо предоставить первый вариант модели.
В использовании уже есть обучающие данные, состоящие из огромного количества объектов и признаков. Что же вам предпринять? Я бы порекомендовал использовать наивный байесовский алгоритм (далее – НБА), т.к. по скорости он опережает большинство других алгоритмов классификации.
Сейчас мы поподробней рассмотрим этот алгоритм, чтобы в вашем распоряжении оказался очень эффективный инструмент обработки большого набора данных. Новичкам в Python также будет полезен готовый код, рассматриваемый в этой статье.
НБА – это алгоритм классификации, в основе которого лежит теорема Байеса. Ее мы рассмотрим, прежде чем переходить к изучению алгоритма.
Теорема Байеса позволяет определить вероятность того или иного события при условии наличия другого статистически связанного с ним.
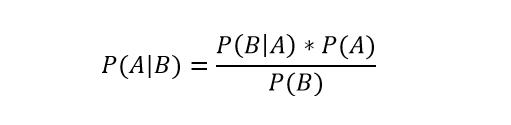
В этом выражении, используя теорему Байеса, мы сможем найти вероятность А при случившемся B. То есть A – будет гипотезой, а B — признаком
P(B|A) – это вероятность B, при которой A будет истиной.
P(A) и P(B) – это независимые вероятности А и В
Концепция НБА
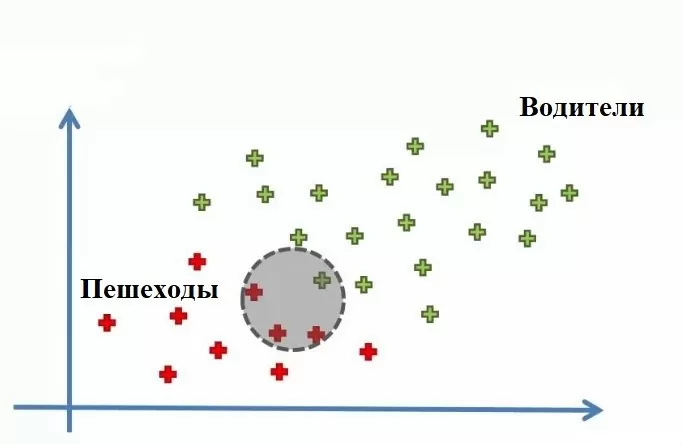
Давайте рассмотрим концепцию наивной теоремы Байеса на примере. Допустим, у нас есть датасет сотрудников компании, и наша цель — создать модель, определяющую способ перемещения до работы сотрудника (пешком или на машине) в зависимости от его дохода и возраста.
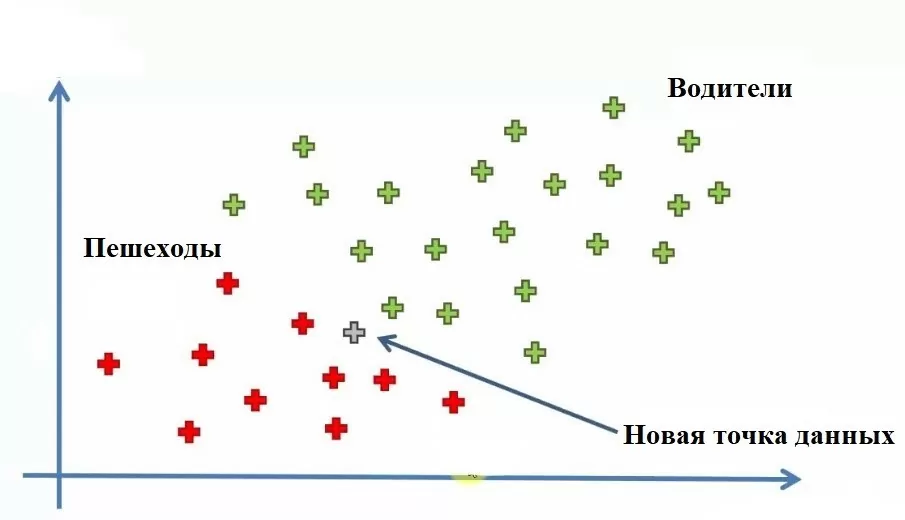
Мы видим 30 точек данных, где красные – ходят пешком (пешеходы), а зеленые – ездят на машине (водители). Теперь давайте добавим еще одну новую точку. И нашей задачей станет нахождение категории для этой новой точки.
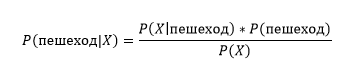
P(пешеход|X) – апостериорная вероятность,
P(X│пешеход) – правдоподобие,
P(пешеход) – априорная вероятность гипотезы,
P(X) – априорная вероятность признака.
Отметим, что для возраста мы выбрали ось Х, а для дохода – ось Y. Используя НБА, найдем категорию нашей новой точки данных. Для этого определим апостериорную вероятность[1] пешеходов и водителей на наших точках. Апостериорная вероятность для пешеходов для новой точки:
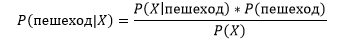
А для водителей соответственно:
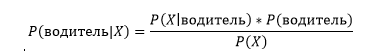
Этапы НБА
Этап 1: Нужно определить все вероятности, необходимые для теоремы Байеса, с целью вычисления апостериорной вероятности.
P(пешеход) – это отношение всех пешеходов и общего количества сотрудников.

Для определения предельной правдоподобности P(X), мы должны сформировать окружность любого радиуса рядом с нашей точкой данных, в которую бы вошли и красные и зеленые точки.

Вычислим P(X|пешеход):

Теперь мы можем найти апостериорную вероятность, используя теорему Байеса:
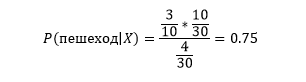
Этап 2: Похожим образом мы найдем апостериорную вероятность для водителей. И это будет 0.25.
Этап 3: Сравнив две найденные вероятности выясним, что P(пешеход|X) имеет большее значение, и новая точка данных принадлежит этой категории.
Реализация НБА
Теперь мы реализуем НБА, используя Python.
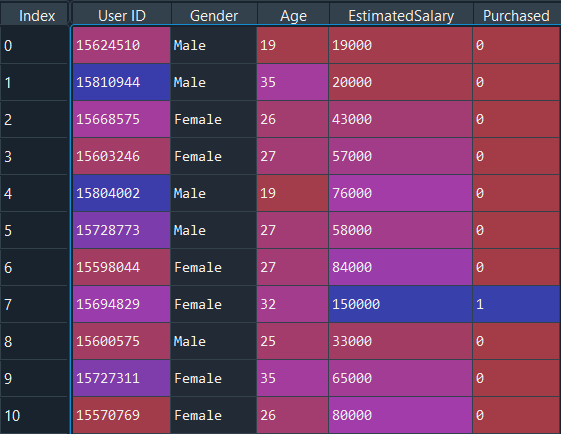
Возьмем датасет из социальной сети, в котором присутствуют данные о пользователях сайта, необходимые для определения условий покупки товара через переход с рекламного баннера, основанный на их доходе, возрасте и поле.
Начнем работу с программой, импортируя необходимые библиотеки.
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import sklearn
Импортируем датасет
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [1, 2, 3]].values
y = dataset.iloc[:, -1].values
Поскольку наш датасет содержит текстовые переменные, необходимо перекодировать его, используя LabelEncoder.
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
X[:,0] = le.fit_transform(X[:,0])
Создаем обучающую и тестовую выборку.
Создаем тестовую выборку на нашем датасете. Размер теста будет 0.20, это означает, что наша обучающая выборка содержит 320 объектов, а тестовая – 80.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)
Масштабирование функций
Теперь мы масштабируем функции для тестовой и обучающей выборки на независимых переменных.
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Обучаем Наивную Байесовскую модель на выборке
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, y_train)
Спрогнозируем результаты теста:
y_pred = classifier.predict(X_test)Прогнозное и реальное значение
y_pred 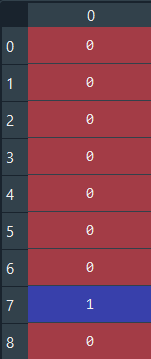
y_test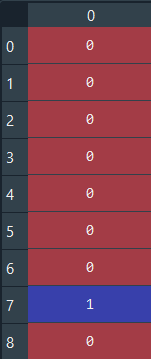
Для первых восьми значений результаты одинаковые. Оценить результат можно, используя матрицу ошибок и показатель точности, сравнивая прогнозируемые и фактические тестовые значения.
from sklearn.metrics import confusion_matrix,accuracy_score
cm = confusion_matrix(y_test, y_pred)
ac = accuracy_score(y_test,y_pred)
Показатель точности — 0.9125
Матрица ошибок:

Точность хорошая, однако, можно добиться лучших результатов, используя другие алгоритмы.
Вывод
В этой статье мы изучили НБА – алгоритм, который чаще всего применяется в задачах классификации.
Основными его преимуществами является простота и способность работать с огромным количеством данных. Сразу после установки НБА можно использовать в работе, а его настройка необходима в очень редком случае.
Несмотря на то, что НБА является хорошим классификатором, значения прогнозных вероятностей не всегда точны. И воспринимать очень серьезно полученные результаты не следует.
Полный код программы:
# Импорт библиотек
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Импорт датасета
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, -1].values
# Разделение датасета на обучающую и тестовую выборку
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.20, random_state = 0)
# Масштабирование функций
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# Обучение наивной модели Байеса на обучающей выборке
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train, y_train)
# Прогноз тестовой выборки
y_pred = classifier.predict(X_test)
# Создание матрицы ошибок
from sklearn.metrics import confusion_matrix, accuracy_score
ac = accuracy_score(y_test,y_pred)
cm = confusion_matrix(y_test, y_pred)
[1] Апостерио́рная вероя́тность — условная вероятность случайного события при условии того, что известны данные, полученные после опыта.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
