Время прочтения: 5 мин.
Использование наивного Байесовского классификатора для фильтрации спама — довольно старый и известный способ фильтрации сообщений. В его основе лежит простая идея – на обучающих данных для каждого слова в сообщении вычисляется оценка вероятности того, что письмо с этим словом является спамом и, исходя их этого, для вновь пришедшего письма на основании всех слов, вычисляется его вероятность оказаться спамом. Это модель предполагает серьезное допущение, что вероятность встретить одно слово не зависит от вероятности встретить другое слово в спамном или неспамном сообщении (отсюда и наивность в названии), однако до сих пор такой классификатор может использоваться и показывать хорошие результаты, даже по сравнению с более продвинутыми методами.
Рассмотрим подробнее как данный алгоритм можно пошагово реализовать на python. Для этого возьмем данные с сайта Kaggle (SMS Spam Collection Dataset). В датасете содержится информация о 5572 сообщений, среди которых 13% спама.
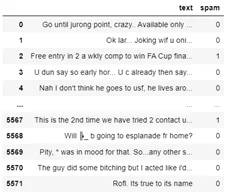
Разделим данные на обучающую и тестовую выборки. Сохраним обучающий датасет в переменную df. Для начала напишем простую вспомогательную функцию для того, что бы получить множество всех слов:
import re
def tokenize(message):
message = message.lower()
all_words = re.findall("[a-z0-9]+", message)
return set(all_words)
Теперь перейдем непосредственно к алгоритму. Для начала для каждого слова нужно найти оценку вероятности встретить его в спамном или неспамном сообщении. Для этого просто посчитаем сколько раз каждое слово встречается в каждом из типов сообщений. Также напишем функцию под это:
from collections import defaultdict
import pandas as pd
def count_words(data):
counts = defaultdict(lambda: [0,0])
for index, row in data.iterrows():
for word in tokenize(row['text']):
counts[word][0 if row['spam'] else 1] +=1
return counts
Воспользуемся этой функцией и сохраним результат в переменную freq:
freq = count_words(df)В результате получаем словарь, следующего вида:
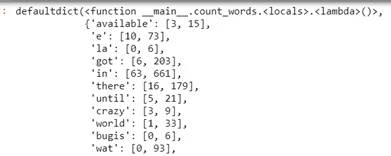
Мы можем видеть каждое слово и сколько раз оно встречается в каждом типе сообщений. Теперь переходим к вычислению веса, то есть нам необходимо поделить конкретную частоту на общее количество сообщений каждого типа. Но здесь есть еще одно допущение. Если какое-то слово присутствует только в сообщениях без спама, то сообщение с этим словом классификатор всегда будет относить к неспамному. Что бы этого избежать при расчете вероятности добавим коэффициент сглаживания равный единицы. Это позволит избежать нулевые вероятности.
Итак идем дальше. Сохраним в переменных общее число сообщений со спамом и без него:
all_spam = df['spam'].loc[df['spam'] == 1].count()
all_not_spam = df['spam'].loc[df['spam'] == 0].count()
Напишем очередную функцию. Она будет возвращать для каждого слова уже посчитанную вероятность:
def prob(freq, all_spam, all_not_spam, k = 1):
return [ (word,
(frequency[0] + k) / (all_spam + 2*k),
(frequency[1] + k) / (all_not_spam + 2*k))
for word, frequency in counts.items()]
Воспользуемся функцией и сохраним результат в переменной result:
result = prob(freq, all_spam, all_not_spam)Получим данные следующего вида:

Теперь мы можем посчитать вероятности для сообщений. Также сделаем это с помощью функции. По идее мы должны перемножить частные вероятностные друг на друга. Но так как вероятности могут представлять собой очень маленькие числа, их перемножение может привести к исчезновению разрядов. Поэтому воспользуемся алгебраическими свойствами и заменим действия на сумму логарифмов:
import math
def final(word_probs, message):
# Также обрабатываются сообщения
message_words = tokenize(message)
# изначально вероятности спама и неспама равны нулю
spam_prob = not_spam_prob = 0.0
# наращиваем вероятности в циклах
for word, prob_if_spam, prob_if_not_spam in word_probs:
# если слово в сообщении используем посчитанную вероятность
if word in message_words:
spam_prob += math.log(prob_if_spam)
not_spam_prob += math.log(prob_if_not_spam)
# если слова нет в сообщении используем вероятность противоположного события, т.е 1 - посчитанная вероятность
else:
spam_prob += math.log(1.0 - prob_if_spam)
not_spam_prob += math.log(1.0 - prob_if_not_spam)
e_spam_prob = math.exp(spam_prob)
e_not_spam_prob = math.exp(not_spam_prob)
# непосредственно формула вероятность по теореме Баейса
return e_spam_prob/(e_spam_prob+e_not_spam_prob)
Из тестового набора данных собираем датасет с вероятностями:
for index, row in test.iterrows():
df_test = df_test.append({'text': row['text'],'prob': final(result, row['text']), 'spam_': row['spam']}, ignore_index=True)
Получаем датасет вида:
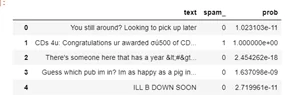
Осталось только поставить порог отнесения к классу на вероятность и проверить работу алгоритма на тестовых данных.
Так как в результате работы предыдущих функций мы получили значение вероятности, от него необходимо перейти непосредственно к метке. Данная функция возвращает метку спама исходя из полученной вероятности:
def func(row):
if row['prob']>0.5:
return 1
else:
return 0
df_test['spam_final'] = df_test.apply(func, axis = 1)
accuracy_score(df['spam'], df['spam_final'])
Для работы этой функции необходимо выбрать порог по которому по вероятности будет присваиваться метка. От выбора этого порога будет зависеть направленность фильтра. Если выбрать минимальный порог, то любое подозрительное сообщение будет отправляться в спам, а это означает что некоторое число «хороших» сообщений будут отнесены в спам. Если выбрать слишком высокий порог, то некоторое число спамных сообщений все же сможет обойти фильтр. Таким образом порог следует выбирать исходя из того, ошибки какого типа для нас в данном случае более приемлемы.
Посмотрим как это будет работать при изменение порога. Для начала попробуем установить порог ровно посередине вероятности – 50%. Для порога в 50% точность составила 76,88%. Попробуем немного сдвинуть. Повторим те же действия для порога в 60% и получим точность уже 98,42%. Получаем очень хороший результат для такой простой модели.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
