Время прочтения: 5 мин.
Дерево решений, как гласит «Википедия» – это средство поддержки принятия решений, использующееся в машинном обучении, анализе данных и статистике. Более простыми словами, дерево решений – это способ разбиения информации на группы для более удобной классификации.
Посмотрим, как дерево решений работает на тривиальном примере. Мы будем определять вероятность того, что заданная машина сломана, на основе следующих данных:
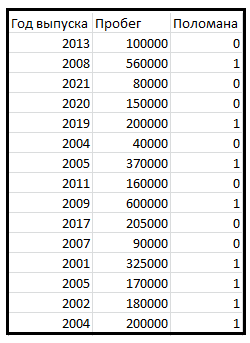
Для простоты понимания работы дерева решений будем рассматривать эту задачу на основе всего двух параметров: «Год выпуска» и «Пробег». Расположим наши данные на точечном графике.
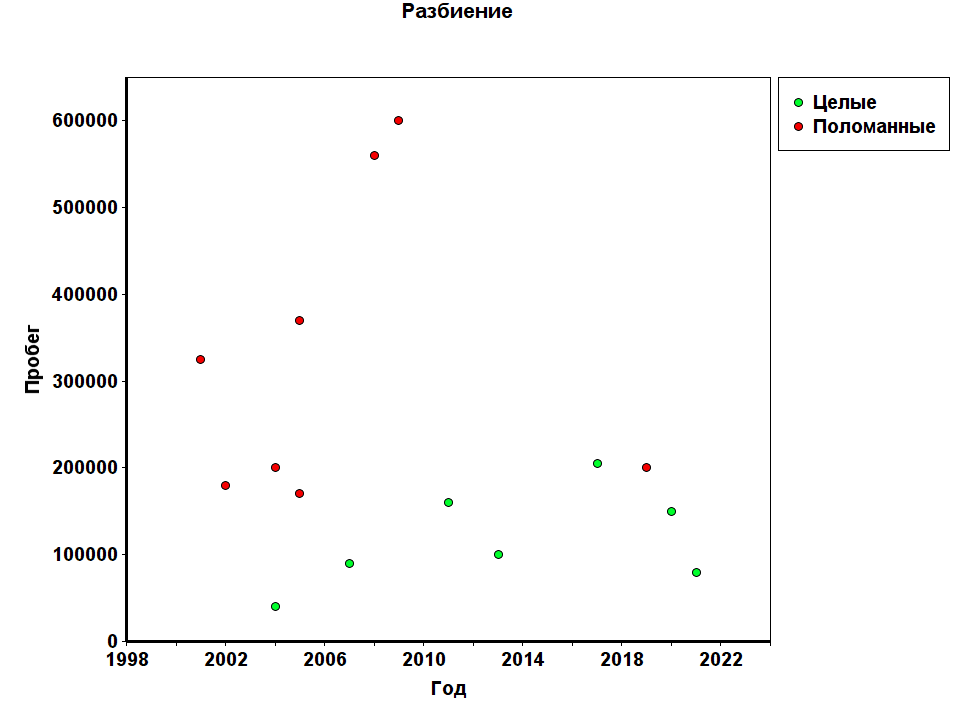
На графике видно, что наши данные эффективно будет разбить по пробегу на группы до 165 тысяч и более 165 следующим образом:
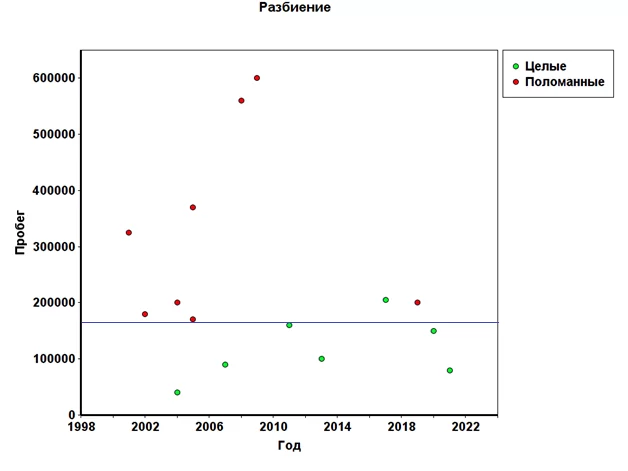
Целью разбиения было получение чистого множества. В данном случае все автомобили с пробегом менее 165 тысяч целы. Таким образом, мы получили чистое множество.
Чистым множеством называется множество, энтропия которого равна 0.
Энтропия – это мера неопределённости некоторой системы, которая колеблется от 0 до 1. Другими словами, чем ближе энтропия к 0, тем большая часть данных принадлежит к одной и той же группе. Энтропия вычисляется по формуле:
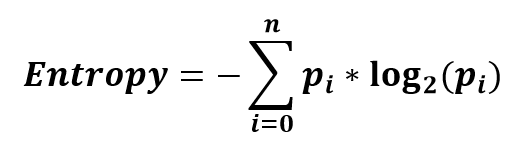
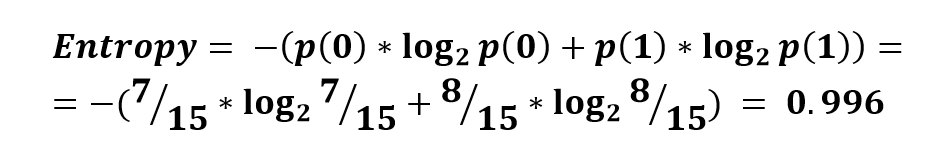
Как мы видим, у исходного множества довольно высокая энтропия. Это говорит о том, что оно достаточно хаотичное.
Итак, после первого разбиения мы получили следующее дерево:
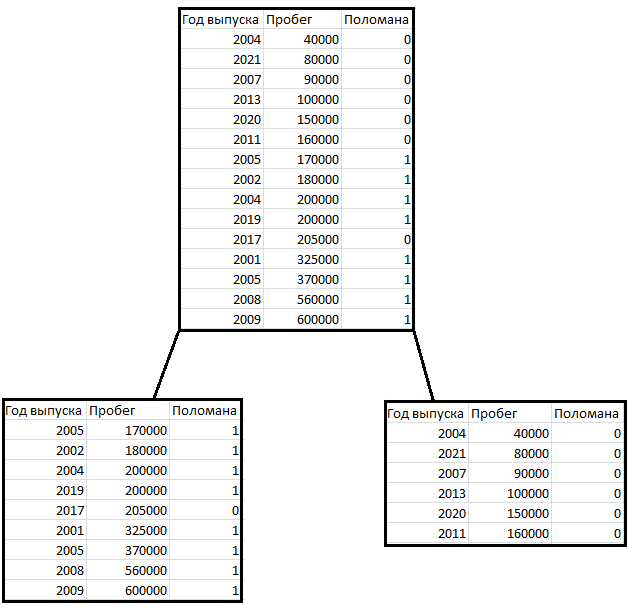
Справа получилось чистое множество. В данном случае мы визуально разделили данные по графику и получили требуемый результат. Далее, для выбора параметра, по которому планируется проводить разбиение, будем использовать понятие информационного выигрыша.
Информационный выигрыш используется для получения максимальной информации о классификации, основываясь на энтропии. Вычисляется по формуле:
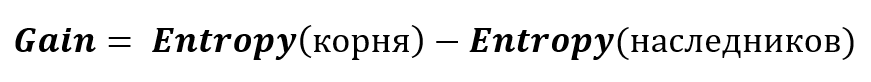
Рассчитаем информационный выигрыш для нашего разбиения:
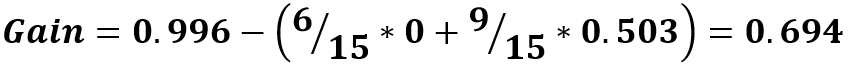
Теперь для сравнения рассчитаем информационный выигрыш для разбиения по 2010 году выпуска:
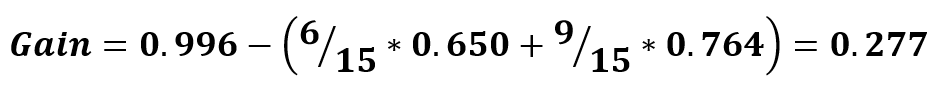
Как мы можем заметить, разбиение по пробегу действительно эффективнее, поэтому его мы и будем использовать на первой итерации.
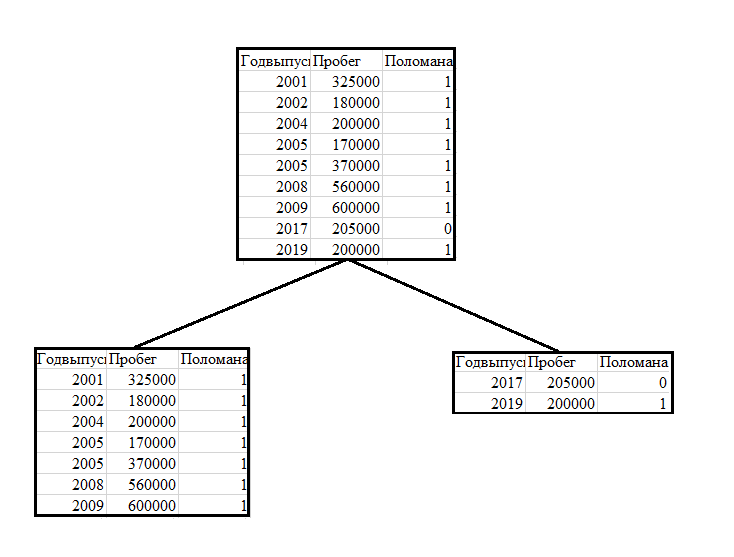
Разбиение левой таблицы производилось по году выпуска автомобиля на группы «до 2016 года» и «после 2016 года»
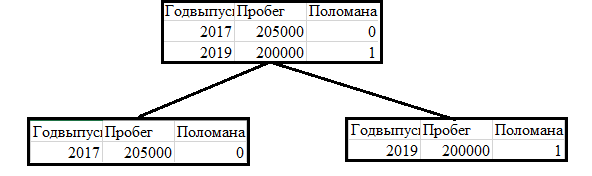
В данном случае разбиение снова произошло по году выпуска. После всех разбиений, дерево выглядит так:
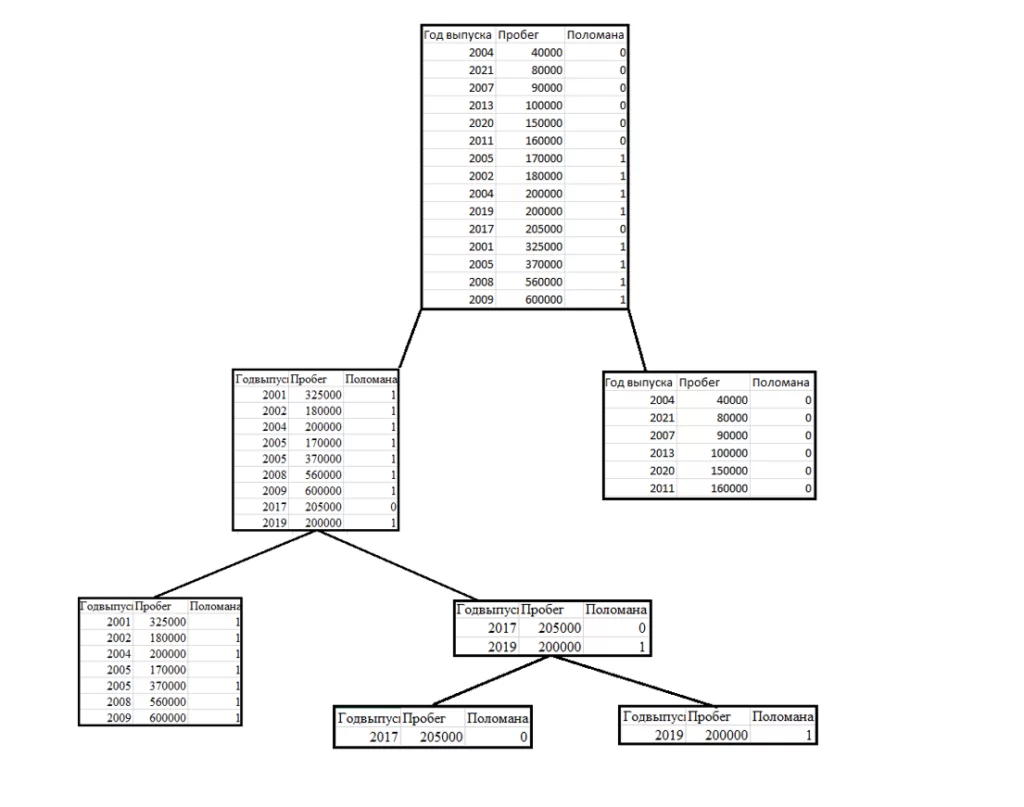
Необходимо так же упомянуть об ещё одном важном параметре – индексе Джини. Он позволяет оценить, насколько правильно, на основе текущих данных, будет определена принадлежность элемента к той или иной группе. Индекс Джини рассчитывается по формуле:
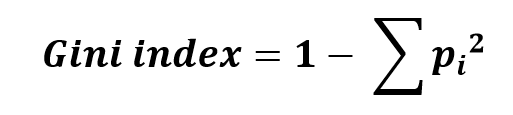
Ради примера рассчитаем индекс Джини для левого узла первого разбиения:
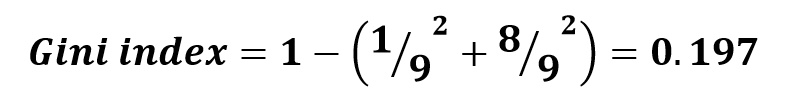
Теперь перейдём к практике.
Реализуем то же самое через популярную библиотеку для Python – Scikit-learn (sklearn). Эта библиотека является одной из самых популярных для Data Science и Machine Learning. Она предоставляет различные алгоритмы для решения задач классификации, регрессии и кластеризации. Это простой и эффективный инструмент для предиктивного анализа данных. Подключаем все необходимые библиотеки:
Считываем данные из файла и разбиваем на две группы: атрибуты и результат, зависящий от этих атрибутов.

Теперь заведём переменную model, которая будет являться объектом дерева решений, и сразу передадим дереву данные, по которым оно будет строиться.

Теперь попробуем предсказать, будет ли поломана машина 2013 года с пробегом 600 тысяч.
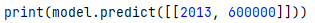
Дерево выдало ответ «0», что соответствует поломанной машине. Теперь для наглядности давайте выведем полное дерево.

Получилось такое дерево условий:
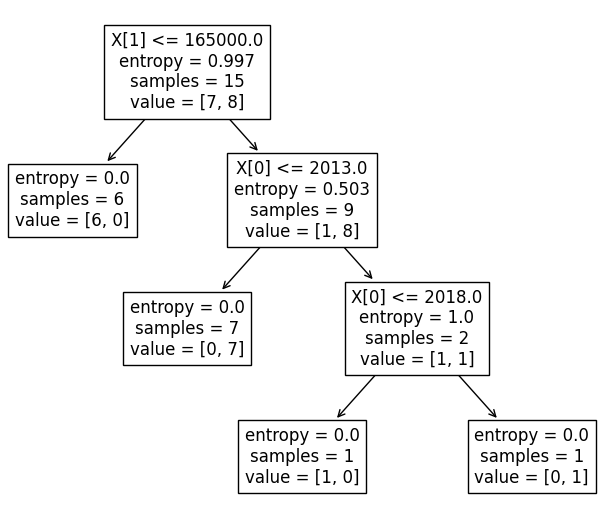
По нему мы можем посмотреть, как именно дерево определяет принадлежность элемента к тому или иному классу. Благодаря тому, что изначальный набор данных у нас был небольшой, дерево тоже получилось не сложным.
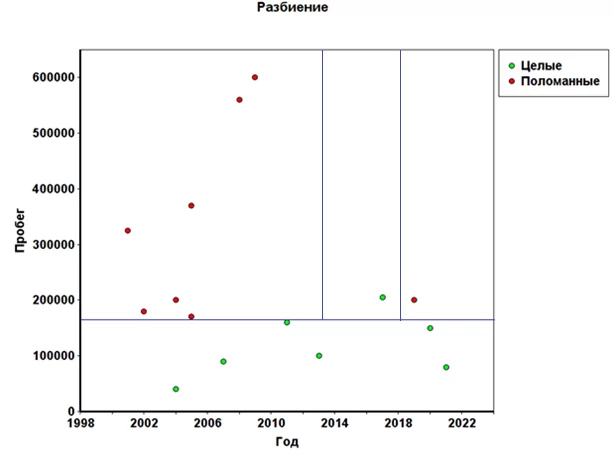
На нашем изначальном графике это будет выглядеть примерно так.
Теперь попробуем на примере, больше приближённом к реальности. Будем предсказывать, будет ли одобрена кредитная карта по двум параметрам: возраст и среднемесячный доход. Наша выборка будет составлять 1320 элементов.
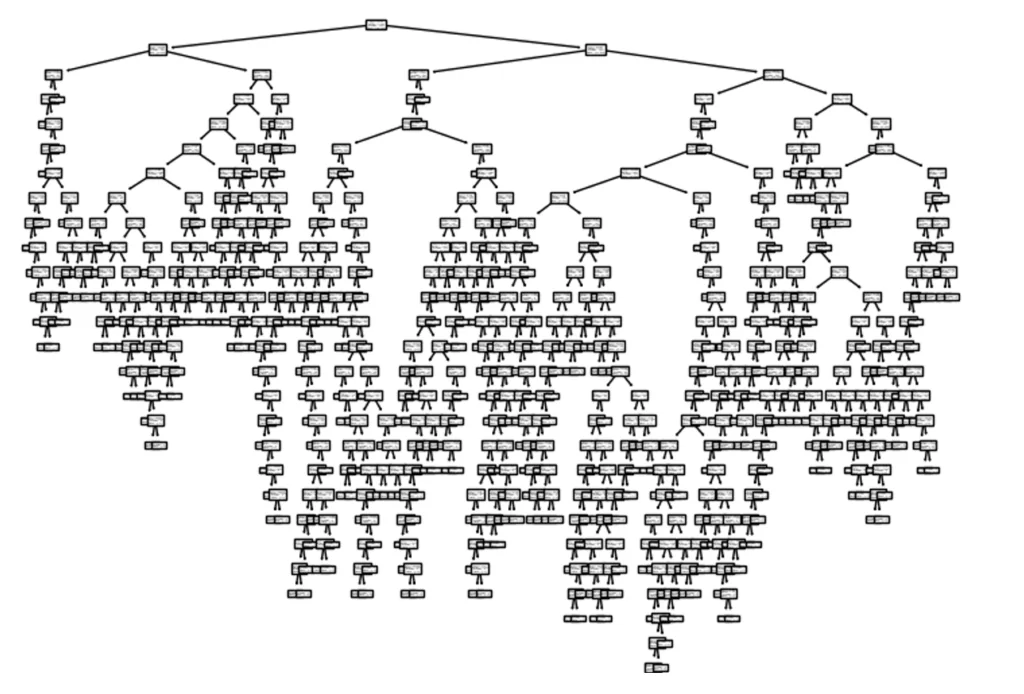
Как можно заметить, это дерево немного сложнее предыдущего. Важно отметить, что с увеличением выборки качество и точность предсказаний возрастает, однако сложность самого дерева и затраты ресурсов так же увеличатся.
Заключение
Как мы можем видеть, всё дерево решений рассчитывается и строится на основе теории вероятностей. Конечно, дерево решений далеко не идеально справляется с задачей классификации, однако на его основе создан более совершенный алгоритм – случайный лес. Но это уже тема для другой работы.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
