Время прочтения: 5 мин.
Метод Дейкстры – метод, базирующийся на графах, который был создан нидерландским научным работником Эдсгером Дейкстрой в 1959 г.
Алгоритм Дейкстры лежит в основе множества востребованных и актуальных современных сервисов, к числу которых также относятся задачи GPS навигации и маршрутизации состояния канала сетевого уровня, оценки процесса движения различного рода систем. Чтобы понять базовую структуру обработки алгоритма, разберем, что именно делает сам алгоритм, каким образом он работает и достигает цель. Рассмотрим, как это можно реализовать с помощью скриптового языка Python с помощью библиотеки networkx.
С помощью данного метода возможно отыскать самые короткие пути от одной из вершин графа до абсолютно всех других. Метод способен функционировать только для графов, рёбра которых никак не имеют отрицательного веса.
Задача поиска кратчайшего пути на картах типа YandexMaps между координатами точек адресов реализуется также с помощью алгоритма Дейкстры.
Перейдем к теории:
Перед нами стоит задача поиска минимального расстояния от одной из вершин графа G (E, V) до всех других вершин, в нашем случае минимальное расстояние между координатами на карте.
Алгоритм Дейкстры может находить кратчайший путь между двумя вершинами графа. Таким образом, если модель графа представлена в виде математической задачи или имеет заложенные математические формулы, то с использованием алгоритма Дейкстры есть возможность найти кратчайший путь между вершинами этого смоделированного графа.
Визуально перенесем географическую карту на координатную плоскость и найдем решение в стандартной координатной плоскости, а после всех преобразований – обратно заменим данные на географические координаты. Следовательно, обозначим множество всех ребер графа G — E (проходы между двумя точками на карте), V – множество всех вершин графа G (являются точками карты, между которыми мы хотим найти наименьшее расстояние)
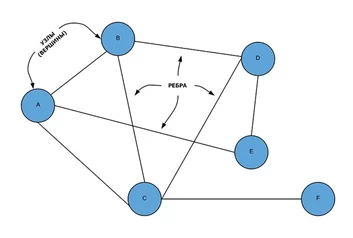
Для каждой вершины из множества V сопоставим конкретную метку — минимальное известное расстояние от этой вершины до α. Метка самой вершины α полагается равной 0, метки остальных вершин – бесконечности.
Все это говорит о том, что расстояния от альфы до других вершин пока неизвестны. Все вершины графа являются не посещёнными и обозначаются как не посещённые.
При работе алгоритма последовательно на каждом шаге можно посетить только одну вершину и пытаться уменьшать метки. Работа алгоритма завершается при условии, когда все вершины посещены.
Ниже представлен Алгоритм Дейкстры с использованием библиотеки networkx:
Импортируем модуль networkx и присвоим ему обозначение nx. Скрипт, с помощью которого можем реализовать алгоритм Дейкстры представлен ниже, суть алгоритма заключается в том, что мы хотим найти кратчайший путь от вершины s до вершины v – shortest_path_s_v. Задаем граф матрицей векторов, с определенным количеством ребер, имеющим свой вес – переменная edges, а также список всех весов ребер заданного графа G weights. Через draw_networkx можем отрисовать заданный нами граф и получить кратчайший путь от вершины s до вершины v, который подсветим красным цветом edge_color=’r’.
import networkx as nx
G = nx.DiGraph()
G.add_weighted_edges_from([
('s', 'u', 10), ('s', 'x', 5), ('u', 'v', 1), ('u', 'x', 2),
('v', 'y', 1), ('x', 'u', 3), ('x', 'v', 5), ('x', 'y', 2),
('y', 's', 7), ('y', 'v', 6)])
predecessors, _ = nx.floyd_warshall_predecessor_and_distance(G)
shortest_path_s_v = nx.reconstruct_path('s', 'v', predecessors)
edges = [(a,b) for a,b in zip(shortest_path_s_v, shortest_path_s_v[1:])]
weights = nx.get_edge_attributes(G, 'weight')
pos = nx.circular_layout(G)
nx.draw_networkx(G, pos=pos)
nx.draw_networkx_edge_labels(G, pos, edge_labels=weights)
nx.draw_networkx_edges(G, pos=pos, edgelist=edges, edge_color="r", width=3)
title = "Shortest path between [{}] and [{}]: {}"\
.format("s", "v", " -> ".join(shortest_path_s_v))
plt.title(title)
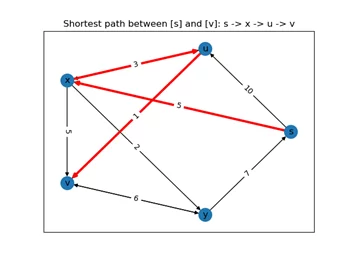
В качестве входной информации существуют 2 точки среди которых мы стремимся найти кратчайший путь, проходя по которому будут задействованы другие точки графа. А также у нас есть карта, которая представляет собой массив векторов из точек координат. Векторная карта представляет собой взвешенный граф, в качестве ребер которого выступают векторы, а их концы можно рассматривать в качестве узлов.
Поскольку дорога представляет собой некоторый набор векторов, соединенных концами(точками), и можно заметить, что большинство узлов на карте имеет два ребра. Не обобщая всё, можно сделать предположение о том, что начальная и конечная точки определяются по широте и долготе пар и соответствуют концам векторов, граф является ориентированным, так как мы переходим из одной точки в другую, тем самым ребра имеют направленность. А плоскость, которая содержит конечные точки(векторы) представляет собой географическую карту.
Простой метод Дейкстры предназначен в целях поиска пути с исходной пункта, либо, иными словами, для реорганизации графа в древо. Для нас отсутствует потребности преобразовывать всю карту в дерево, так как большинство узлов пребывает на значительном отдалении и для повышения производительности метода должны игнорироваться.
Метод Дейкстры также никак не учитывает значимость узлов, полагая все без исключения участки в одинаковой степени значимыми. Поэтому нужно отметить, что возможность применения метода Дейкстры допускает также необходимость улучшения ради более конкретных расчетов расстояний, если в заложенном алгоритме будут использованы погрешность качества дорог, пробок, объездных путей и пр. факторов, которые имеют значение в реальном времени.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
