Время прочтения: 5 мин.
В современном мире траты на электроэнергию несут особый вес в расходах любой фирмы, любой компании, поэтому так важно вовремя выявлять аномалии и проверять вызывающие их причины. В данном исследовании мы будем решать задачу поиска аномалий, какое значение они несут для данных, и наблюдать, как их удаление влияет на изначальную выборку.
Анализ начинается с импорта некоторых библиотек, загрузки файлов с данными, очистки данных от пустых строк и их вывод на экран:
import pandas as pd
import statistics as st
import numpy as np
import matplotlib.pyplot as plt
dataset = pd.ExcelFile(r" Эл.xlsx")
dataframe = dataset.parse('Итог')
dataframe=dataframe.dropna()
dataframe.head()
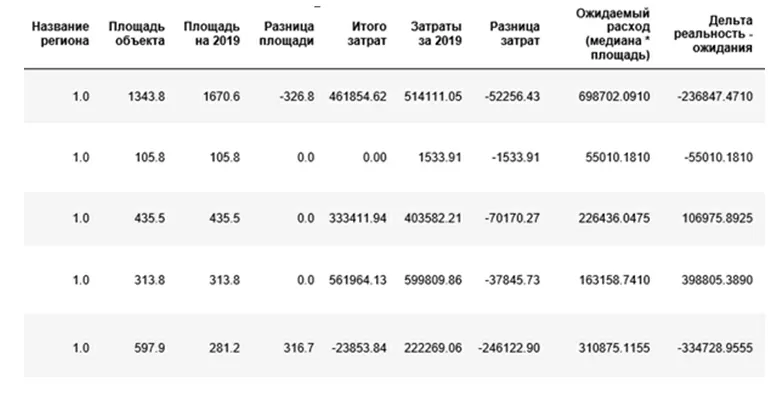
Как видно, наша выборка несет в себе данные отделений, их площадь и затраты на электроэнергию. Регионы специально приведены к численной форме для защиты внутренних данных и удобства возможных исследований. Также имеются приблизительные расчеты ожидаемых расходов и разницы с реальностью, посчитанные до этого в Excel.
Но вернемся к Python. Следующим шагом визуализируем отношение друг к другу множества затрат и множества площадей:
fig, axis_money = plt.subplots()
axis_size = axis_money.twinx()
axis_money.plot(dataframe['Итого затрат'], 'ro', color='green')
axis_size.plot(dataframe['Площадь объекта'], 'ro', color='orange')
plt.show()
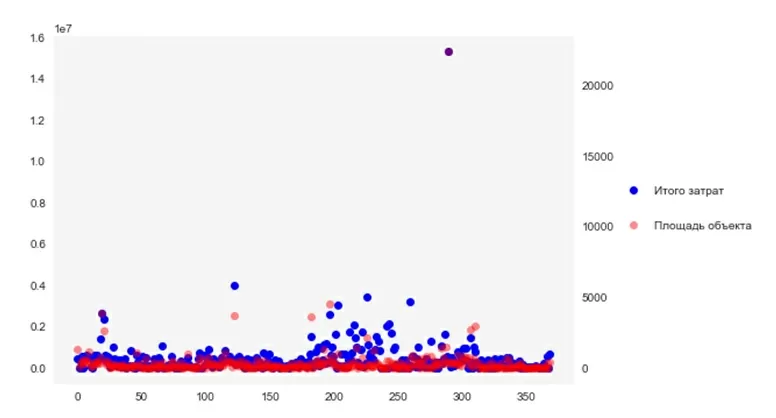
Как мы можем увидеть из графика – в некоторых местах у нас имеются сильные расхождения между затратами на объект и его площадью. Создадим и используем функцию, чтобы сравнить доверительные интервалы показателя «затраты/площадь» за 2019 и 2020 год:
import scipy.stats as sd
def find_interval(data):
a=1.0*np.array(data)
interval = sd.t.interval(0.95, len(a)-1, loc=np.mean(a), scale=sd.sem(a))
print('Доверительный интервал Электричество/Площадь:', interval)
payfor=dataframe['Итого затрат']/dataframe['Площадь объекта']
find_interval(payfor_2020)

payfor_2019=dataframe['Затраты за 2019']/dataframe['Площадь на 2019']
find_interval(payfor_2019)

По этому показателю мы будем определять неопределенность наших оценок. Как видно, доверительный интервал за 2019 год не особо велик, но разница за 2020 год примерно 770, что может натолкнуть на мысль о наличии аномальных значений. Дополнительно, для лучшего понимания характеристик выборок, найдем среднее, медиану, моду, дисперсию и среднеквадратическое отклонение:
mean_2020 = payfor_2020.mean()
median_2020 = payfor_2020.median()
mode_2020 = payfor_2020.mode()[0]
dis_2020 = st.variance(payfor_2020)
sqo_2020 = np.sqrt(dis_2020)
print(mean_2020, median_2020, mode_2020, dis_2020, sqo_2020)

mean_2019 = payfor_2019.mean()
median_2019 = payfor_2019.median()
mode_2019 = payfor_2019.mode()[0]
dis_2019 = st.variance(payfor_2019)
sqo_2019 = np.sqrt(dis_2019)
print(mean_2019, median_2019, mode_2019, dis_2019, sqo_2019)

Значения среднеквадратического отклонения (1743; 3796) также ведут к необходимости чистки выборки. Как известно, самый простой способ выявления аномалий – это поиск значений, которые больше среднеквадратического отклонения в три раза. Основываясь на этих знаниях, пишем функцию:
anomalies = []
def find_anomalies(data):
data_std = np.std(data)
data_mean = np.mean(data)
anomaly_cut_off = data_std * 3
lower_limit = data_mean - anomaly_cut_off
upper_limit = data_mean + anomaly_cut_off
print(lower_limit)
print(upper_limit)
for outlier in data:
if outlier > upper_limit or outlier < lower_limit:
anomalies.append(outlier)
return anomalies
И используем её на практике:
var2020 = find_anomalies(payfor_2020)
print(var2020)

anomalies.clear()
var2019 = find_anomalies(payfor_2019)
print(var2019)

Первая строка в получаемых данных – нижняя «нормальная» граница, вторая строка – верхняя. Однако, в силу генезиса распределения, отрицательных значений мы иметь не можем. Поэтому, на выходе получаем пять аномальных значений в 2020 году и четыре аномальных значения в 2019. Для аудитора – это найденные вопросы, требующие изучения. Для математика – проблема, которая мешает давать выборке адекватные оценки.
Взяв данные на заметку, удаляем их и перепроверяем получаемые значения:
2020 год:

2019 год:

Как видим, нам удалось уменьшить доверительные интервалы и сгладить «разброс» выборки. Что это нам дало? Во-первых, позволило выявить подозрительные случаи в большом объеме данных, во-вторых, позволило приблизить будущие прогнозные данные к реальным.
Так, к примеру, среднее значение «затраты/площадь» у 2020 года неочищенной выборки было 1694, а у 2019 – 1984.
Проведем прикидочные расчеты: допустим, в час тратится 100 ватт, объект работает 9 часов в день, в среднем 30 дней в месяц, в году – 12 месяцев. Перемножаем: a=100*9*30*12=324 000 ватт=324 кВатт. Допустим, что, в среднем, цена на кВатт – 5 рублей. Перемножаем: 5*324=1620.
Теперь рассмотрим тот же самый параметр у очищенной от аномалий выборки:
2020 – 1558, 2019 – 1643.
Сведем данные в таблицу:
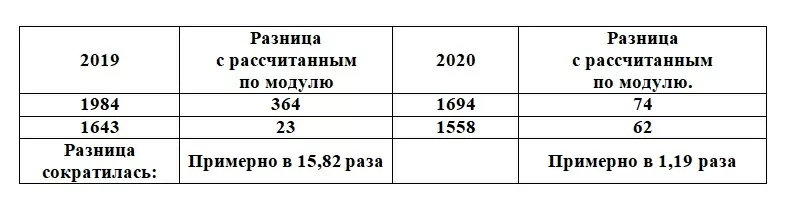
Возможно, удаление аномалий и не оказало такого действия на 2020 год, но уменьшение разницы с рассчитанным значением в 15,82 раза в 2019 году – отличный результат.
Создание инструмента поиска аномалий считается успешным, а данные по затратам на электроэнергию отправляются ждать дальнейших исследований.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
