Время прочтения: 4 мин.
При построении нейронных сетей перед нами часто встаёт вопрос правильного выбора функции потерь, используемой для формирования соответствий между входными и выходными параметрами. Функция потерь отвечает за оценку того, насколько хорошо модель предсказывает реальное значение, и построение модели сводится к решению задачи минимизации значения этой функции на каждом этапе. И в зависимости от того, как выглядят наши данные, требуется использовать разные подходы.
В рамках данной статьи мы рассмотрим три функции потерь для нейронных сетей, решающих регрессионные задачи.
Mean Squared Error
Среднеквадратичная ошибка (MSE) — одна из основных функций расчёта отклонения. Для каждой точки вычисляется квадрат отклонения, после чего полученные значения суммируются и делятся на общее количество точек. Чем ближе полученное значение к нулю, тем точнее наша модель. Данный метод расчёта в значительной мере чувствителен к выбросам в выборке, или к выборкам где разброс значений очень большой. В основном, данная функция применяется для переменных, распределение которых близко к распределению Гаусса.
Mean Absolute Error
Средняя абсолютная ошибка (MAE) – это усреднённая сумма модулей разницы между реальным и предсказанным значениями. MAE во многом похожа на MSE, но она отличается меньшей чувствительностью к выбросам значений (так как не берётся квадрат отклонения).
Mean Squared Logarithmic Error
Среднеквадратичная логарифмическая ошибка (MSLE) – усреднённая сумма квадратов разностей между логарифмами значений. Благодаря большому гасящему эффекту логарифма она более применима к моделям, строящимся на данных, которые имеют большой разброс значений на несколько порядков.
Продемонстрируем как выбор функции потерь влияет на процесс построения нейронной сети. Для генерации данных будем использовать встроенную в scikit-learn функцию make_regression, а в качестве нейронной сети будет выступать многослойный перцептрон.
Код используемый для демонстрации:
from sklearn.datasets import make_regression
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
from matplotlib import pyplot
# формирование датасета
X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1)
# нормализация
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(y.reshape(len(y),1))[:,0]
# разделение
n_train = 500
trainX, testX = X[:n_train, :], X[n_train:, :]
trainy, testy = y[:n_train], y[n_train:]
# определение для модели
model = Sequential()
model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(1, activation='linear'))
opt = SGD(lr=0.01, momentum=0.9)
model.compile(loss=вид функции потерь, optimizer=opt)
# расчёт
history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0)
# Оценка качества
train_mse = model.evaluate(trainX, trainy, verbose=0)
test_mse = model.evaluate(testX, testy, verbose=0)
print('Train: %.3f, Test: %.3f' % (train_mse, test_mse))
# plot Демонстрация результата
pyplot.title('Loss / Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='test')
pyplot.legend()
pyplot.show()
В данном коде мы будем заменять только указанный вид функции потерь.
Результат для MSE:
model.compile(loss='mean_squared_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.000, Test: 0.001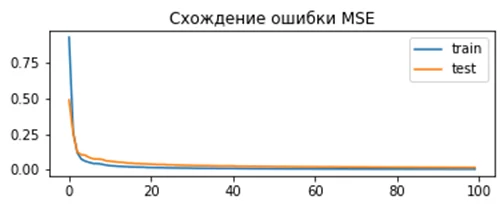
Как видно из графика, модель показывает хорошую сходимость и низкое отклонение.
Результат для MSLE:
model.compile(loss=' mean_squared_logarithmic_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.165, Test: 0.184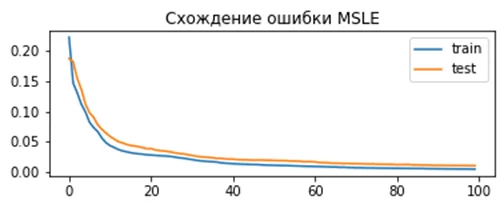
По графику видно, что для данного набора данных MSLE сходится медленней чем MSE. С одной стороны, это может привести к тому что модель будет строиться медленней и получится хуже, с другой – использование MSE может привести к переобучению. Результат для MAE:
model.compile(loss='mean_absolute_error', optimizer=opt)Полученное отклонение для модели:
Train: 0.002, Test: 0.002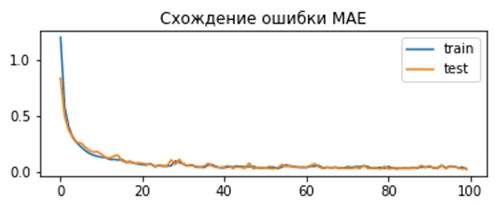
Здесь мы можем увидеть, что результат сходится очень эффективно, но ошибка имеет нерегулярный характер. Так как используемый нами генератор строит гауссово распределение без выбросов, использование MAE не даёт значительных преимуществ.
Очевидно, что от выбора правильной функции потерь сильно зависит точность, качество и скорость построения модели, поэтому следует внимательно подходить к выбору опираясь как на используемую модель, так и на характеристики входных данных.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
