Время прочтения: 3 мин.
В основной своей массе, статьи по machine learning сосредотачиваются на очистке данных, выборе алгоритма для проектирования прогнозирующей функции и первичной оценке качества прогнозирования целевой переменной. Но не менее важным этапом, следующим за уже перечисленными, является мониторинг стабильности новых выборок относительно выборок, участвующих в разработке и в первичной оценке модели.
Одним из решений для оценки изменения популяции является индекс стабильности популяции или population stability index.
Простыми словами, PSI сравнивает распределение переменной в новом наборе данных с набором тренировочных данных, который использовался при разработке модели. Также хотелось бы отметить, что основной сценарий применение алгоритма – оценка изменения распределения на выборке отличной по времени от той на которой проводилась разработка (точное ее название Out Of Time или OOT).
Для описания принципов работы алгоритма был использован учебный набор данных Boston Housing применительно к признаку CRIM. Подробный расчет по данному признаку представлен в таблице ниже.
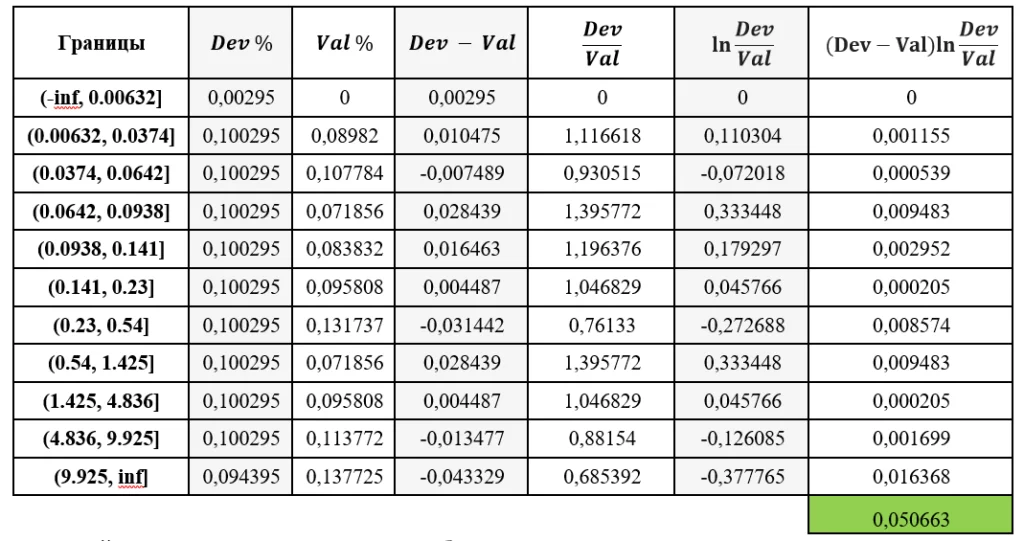
Данный алгоритм предварительно разбивает по-новому датасету признак на интервалы с помощью функции дискретизации на основе квантилей. Затем считаются доли попадания в полученные интервалы по данному признаку как в тренировочном наборе данных, так и в наборе новых данных. Далее ищется разность и отношение между результатами попаданий на тренировочной и новой выборках. Как итог считается PSI на интервалах, как показано в последнем столбце таблицы выше. Результатом работы алгоритма является сумма PSI на интервалах.
Итоговое PSI для примера равен 0,05. Но как интерпретировать данное значение?
Для получения вывода о том, что необходимо делать с моделью нужно использовать следующие интервалы:
- PSI менее 0.1. Изменения в данных незначительны и модель не требует доработки;
- PSI в диапазоне от 0.1 до 0.2. Есть изменения в данных и модель требует незначительной доработки;
- PSI более 0.2. Модель не пригодна для использования. Здесь видятся два варианта исправления ситуации: переобучение модели или замена ее другой.
Визуализацию первых трех этапов работы алгоритма по признаку CRIM, выбранного набора данных, можно увидеть на графике ниже.
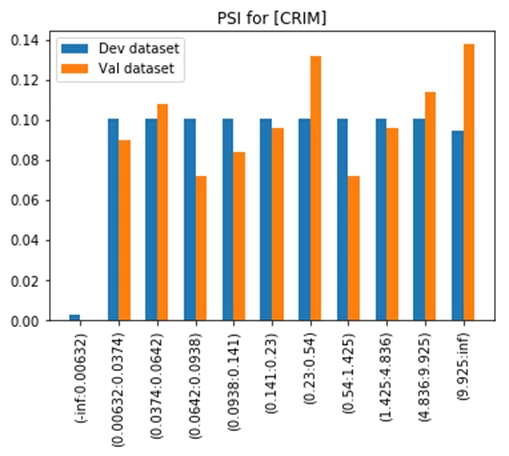
Для реализации алгоритма был написан код на python, который оформлен в виде функции PSI_factor_analysis, где на вход подаются два набора данных и признак, по которому необходимо расчитать PSI. При вызове функции выводится рассчитанный PSI и строится график. Код для данной функции представлен ниже.
def continuous2interval(df, df_target, percent_interval=0.1):
special_target = []
interval_target = []
begin = False
temp_percent = 0
for index, row in (df[df_target].value_counts(normalize=True)).reset_index().sort_values(by='index').iterrows():
if row[df_target] >= percent_interval:
special_target.append(row['index'])
else:
temp_percent += row[df_target]
if begin == False:
begin = row['index']
if temp_percent >= percent_interval:
interval_target.append([begin, row['index']])
begin = False
temp_percent = 0
if begin != False:
interval_target.append([begin, np.inf])
return interval_target, special_target
def PSI_factor_analysis(dev, val, column):
intervals = [-np.inf] + [i[0] for i in continuous2interval(dev, column)[0]] + [np.inf]
dev_temp = pd.cut(dev[column], intervals).value_counts(sort=False, normalize=True)
val_temp = pd.cut(val[column], intervals).value_counts(sort=False, normalize=True)
print('PSI:', sum(((dev_temp - val_temp)*np.log(dev_temp / val_temp)).replace([np.inf, -np.inf], 0)))
plt.bar(np.arange(len(intervals)-1) - .15, dev_temp.values, width=0.3, label='Dev dataset')
plt.bar(np.arange(len(intervals)-1) + .15, val_temp.values, width=0.3, label='Val dataset')
plt.xticks(np.arange(len(intervals)-1), ['({}:{})'.format(i.left, i.right) for i in list(dev_temp.index)], rotation=90)
plt.title('PSI for [{}]'.format(column))
plt.legend()
plt.show()
Таким образом, в данной статье мы рассмотрели принцип работы алгоритма PSI, представили реализацию данного подхода для оценки изменения популяции на языке python и научились оценивать результаты работы алгоритма.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
