Время прочтения: 15 мин.
Введение
Традиционно в машинном обучении, при анализе данных, перед разработчиком ставится проблема построения объясняющей эти данные модели, которая должна сделать жизнь проще и понятней тому, кто этой моделью начинает пользоваться. Обычно это модель некоторого объекта/процесса, данные о котором собираются при регистрации ряда его параметров. Полученные данные, после выполнения различных подготовительных процедур, представляются в виде таблицы с числовыми данными (где строка – объект, а столбец – параметр), которые необходимо обработать, подставив их в те или иные формулы и посчитать по ним, используя какой-нибудь язык программирования.
Одним из часто встречающихся на практике методе, используемый в самых различных его модификациях, является метод наименьших квадратов (МНК). Этот метод был опубликован в современном виде более двухсот лет назад, именно поэтому особенное удивление вызывает то, что этот хрестоматийным метод не описан максимально подробно на самых популярных ресурсах, просвещённых анализу данных. Поэтому разработчик в попытках самостоятельно разобраться с МНК обращается к чтению самых различных бумажных и электронных изданий. После чего желание разобраться быстро улетучивается по причине того, что авторы этих ресурсов особо не «заморачиваются» над объяснениями выполняемых ими преобразований и допущений.
Обычно объяснение метода представляется в виде
1) перегруженной математическими абстракциями «классического описания»;
2) «готовой процедурки», в которой выполняется программная реализация неких конечных выражений, полученных при каких-то начальных условиях.

Первый вид объяснения вызывает полное отторжение у новичка в виду отсутствия должного уровня математической подготовки и представляется непонятным нагромождением формул. А второй вид представляется неким черным ящиком, из которого чудесным образом извлекаются правильные значения. Из чего делается вывод, что все эти «математические изыскания» лишние, а нужно лишь найти на просторах интернета правильную процедуру и «прикрутить» её в проект, где она начинает выдавать значения «похожие на правильные». Подобный ситуативный путь решения проблемы разработчиком приводит к тому, что корректно проверить, модифицировать найденный код не представляется возможным и, соответственно, верифицировать получаемый результат тоже.
Триада
Данные проблемы возникают из-за того, что при описании МНК не описывается путь перехода от математического описания метода к его программной реализации. Данная проблема была давно преодолена одним из отцов основателей математического моделирования в нашей стране академиком Самарским А.А., который предложил универсальную методологию вычислительного эксперимента в виде триады «модель-алгоритм-программа».
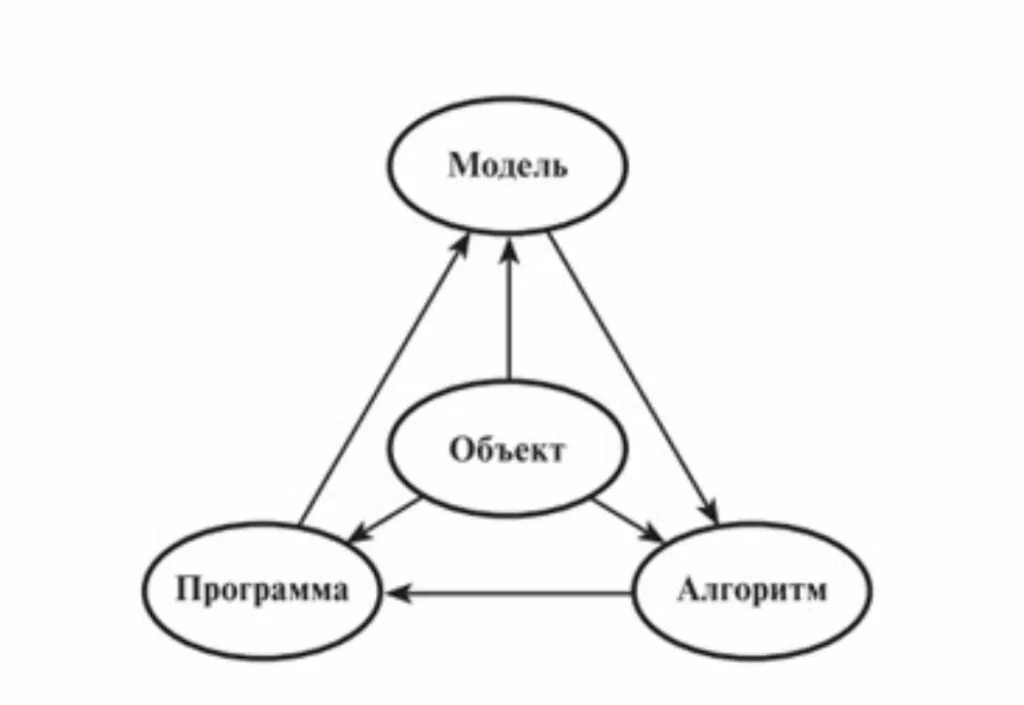
Из предложенной схемы становится видно, что путь от модели объекта к программе лежит через её алгоритмическое описание. Таким образом, в представленной парадигме для детального объяснения МНК нужно
1) описать математическую модель объекта/процесса, анализируемые параметры которой формализуются в виде некой функциональной зависимости;
2) синтезировать алгоритм оценки искомых параметров модели на основе МНК;
3) выполнить программную реализацию полученного алгоритма.
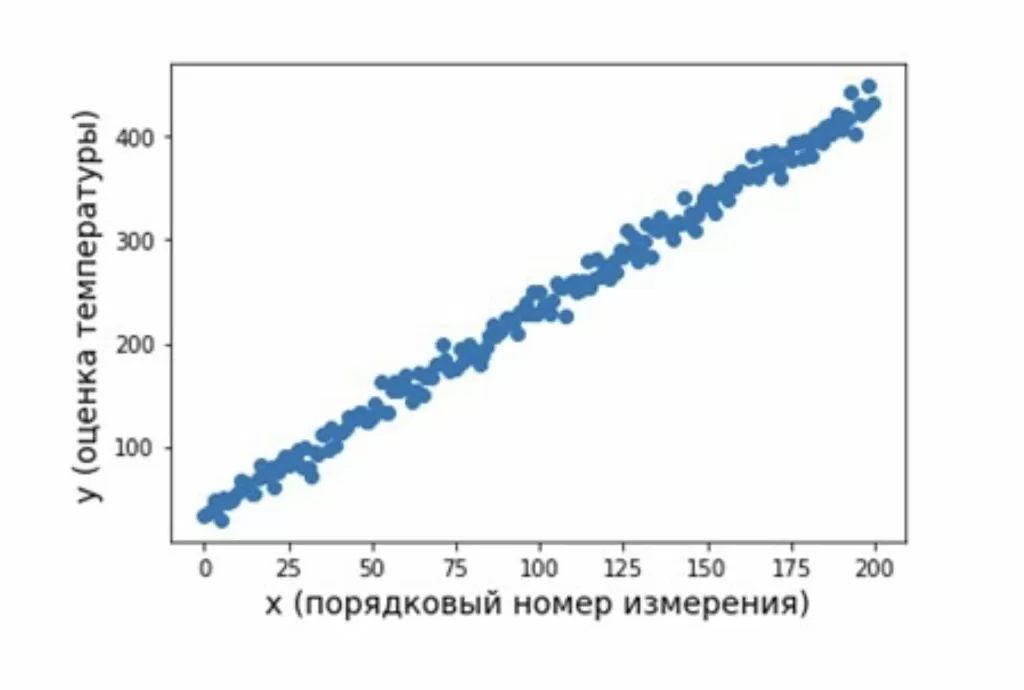
Попробуем абстракции последних абзацев пояснить на примере. Пусть в качестве моделируемого объекта будем рассматривать процесс измерения термометром температуры печи, которая линейно зависит от времени и флуктуирует в области истинного значения по нормальному закону. Необходимо по выполненным измерениям определить зависимость, по которой изменяется температура в печи. При этом ошибка найденной зависимости должны быть минимальной.
В качестве анализируемых данных будем рассматривать n значений температуры, измеренной в градусах, получаемые с использованием термометра и зависящие от времени. Эти данные представим в виде таблицы, где строки – это объекты, первый столбец – набор параметров (j=1), второй столбец – набор измеренных ответов:

т.е. случайная величина, распределённая по закону Гаусса с фиксированным значением среднеквадратического отклонения (СКО), нулевым математическим ожиданием (МО) и с автокорреляционной функцией в виде дельта-функции.
Ниже приведен код генерирующий набор данных на python. Для реализации приведенного в статье кода потребуется импортировать несколько библиотек.
import random
import matplotlib.pyplot as plt
import numpy as np

def datasets_make_regression(coef, data_size, noise_sigma, random_state):
x = np.arange(0, data_size, 1.)
mu = 0.0
random.seed(random_state)
noise = np.empty((data_size, 1))
y = np.empty((data_size, 1))
for i in range(data_size):
noise[i] = random.gauss(mu, noise_sigma)
y[i] = coef[0] + coef[1]*x[i] + noise[i]
return x, y
coef_true = [34.2, 2.] # весовые коэффициенты
data_size = 200 # размер генерируемой набора данных
noise_sigma = 10 # СКО шума в данных
random_state = 42
x_scale, y_estimate = datasets_make_regression(coef_true, data_size, noise_sigma, random_state)
plt.plot(x_scale, y_estimate, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
Сгенерированный набор данных будет иметь вид
Математическая модель
Далее математическая модель будет описана три раза. Последовательно уровень абстракции при описании модели будет понижаться и конкретизироваться. Эти описания приведены для того, чтобы в дальнейшем материал, приведенный в статье, можно было соотнести с классическими изданиями.
Первое описание математической модели. Самое общее.
Поскольку мы рассматриваем процесс, который связывает набор наблюдаемых параметров и измеренных ответов с минимальной ошибкой этой связи, то математическую модель этого процесса в общем виде можно представить

Второе описание математической модели. Общее описание линейной модели.
Поскольку по условию задачи мы рассматриваем линейную зависимость, на которую влияет шум, имеющий нормальное распределение с нулевым средним значением, то используем линейную относительно параметров модель, а метрикой выберем расчёт СКО ошибки

Третье описание математической модели. Модель конкретизирована под условия примера.
Поскольку по условию задачи мы рассматриваем линейную зависимость одного параметра (поскольку j=1, то далее эту зависимость при описании опустим), на оценку которого влияет шум, имеющий нормальное распределение, то используем линейную модель с двумя коэффициентами

Обсуждение моделей
Было рассмотрено три модели, описывающие процесс изменения температуры в печи. Первая модель описана в наиболее общем виде, а третья приведена в виде, наиболее соответствующем начальным условиям задачи. В третьей модели учтен линейный закон изменения температуры (используется линейная модель) и нормальный закон распределения шума в измерениях (используется квадратичная функция ошибки).
Хочется отметить, что параметры математической модели процесса изменения температуры, описанной в выражении (2), в принципе, могут находиться не только методом наименьших квадратов, поскольку метрика с квадратичной функцией ошибки в явном виде не прописана. Такая общая форма записи приведена, поскольку не представляется возможным в кратком виде привести все возможные модификации МНК, у которого минимизация для различных условий может выполняться также различно.
В выражениях (3) и (4) линейные модели отличаются только количеством учитываемых параметров, причем третья модель – это редуцированная вторая модель, у которой только два коэффициента (один свободный и один весовой коэффициенты).
Далее с использованием выражения (4) и МНК, синтезируем алгоритмы, оценивающие параметры модели.
Алгоритмы и реализующие их программы
Далее будут выведены три алгоритма, результат работы которых позволит определить зависимость изменения температуры печи от времени. Последовательно сложность конечных выражений, используемых в алгоритмах, будет понижаться. Эти алгоритмы приведены для того, чтобы полученные выражения, можно было соотнести с классическими изданиями.

Начнем с применения правила дифференцирования функции представленной в виде суммы
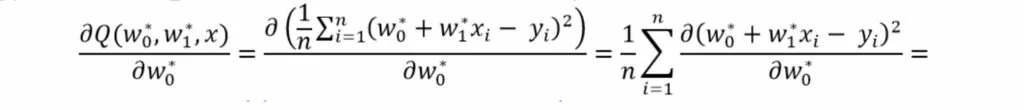
применим правило дифференцирования сложной функции
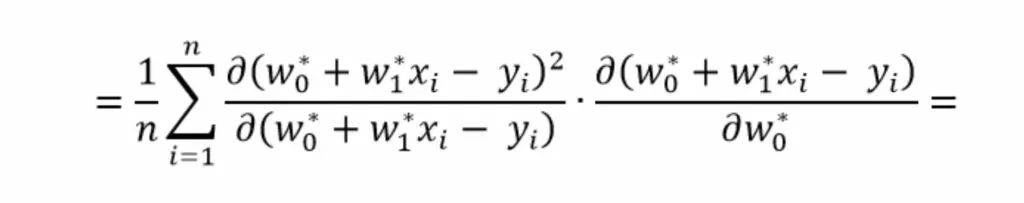
применим правило дифференцирования функции представленной в виде суммы
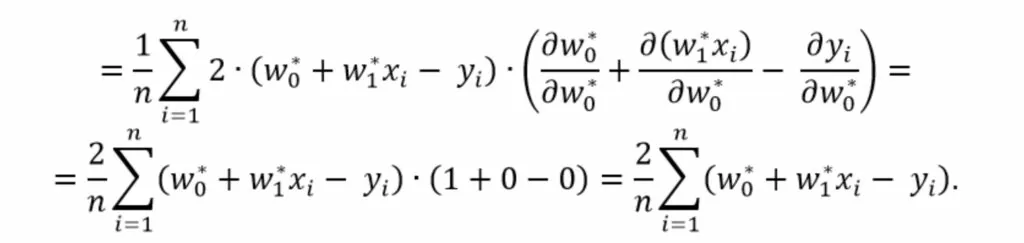

применим правило дифференцирования функции представленной в виде суммы
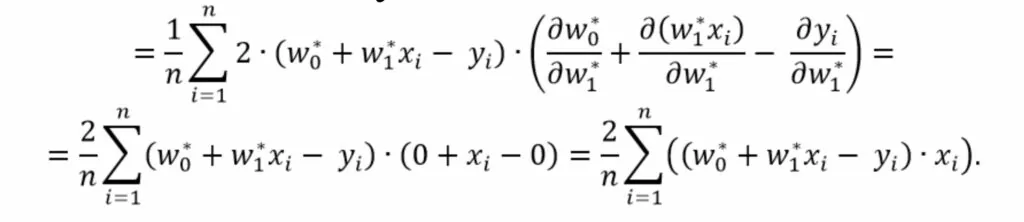
Приравняем полученные производные к нулю и решим полученную систему уравнений
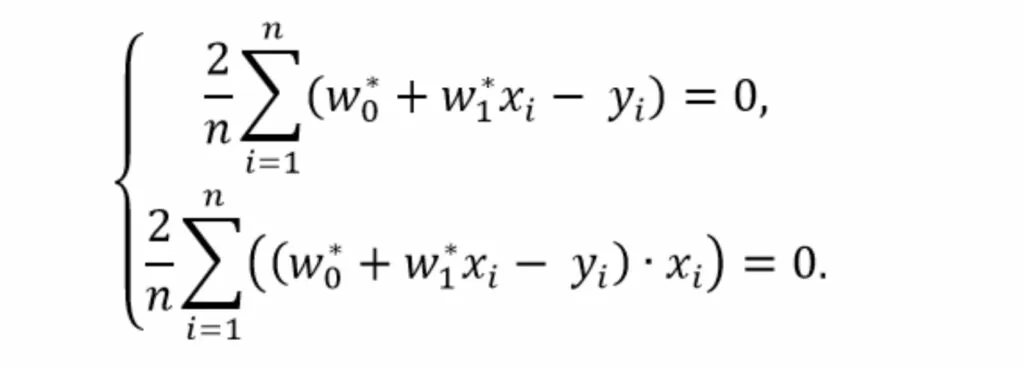
Раскроем скобки
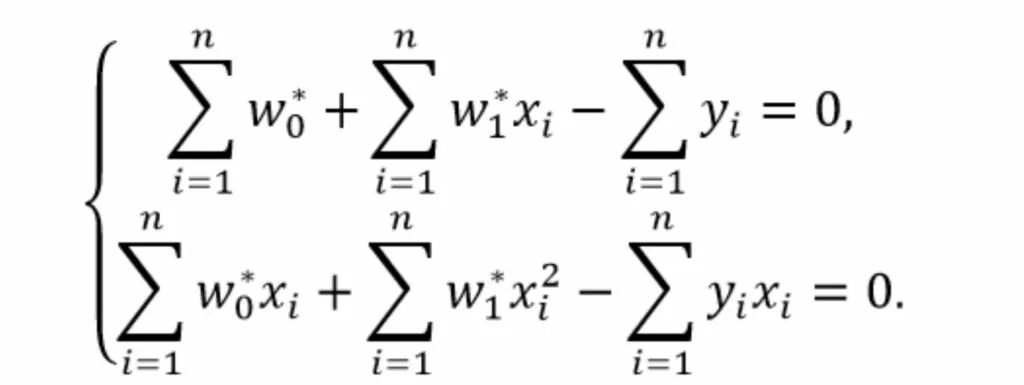
Вынесем постоянные множители за скобки
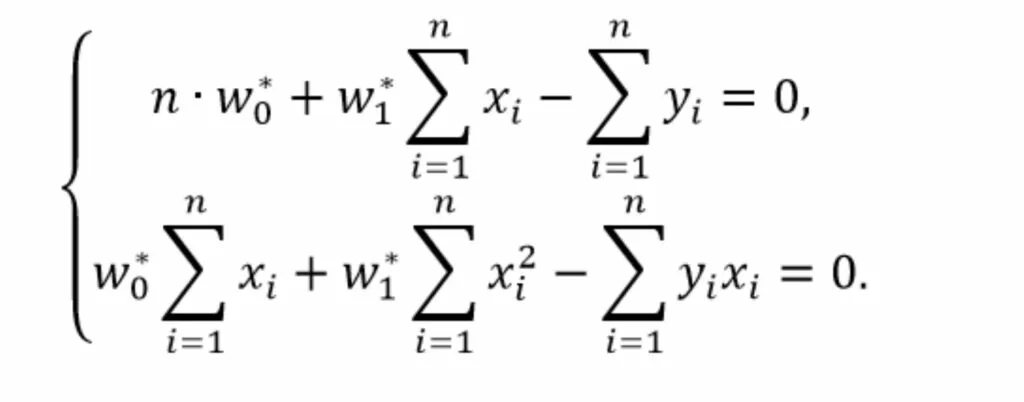
Вынесем слагаемые с множителем «y» в правую часть уравнений
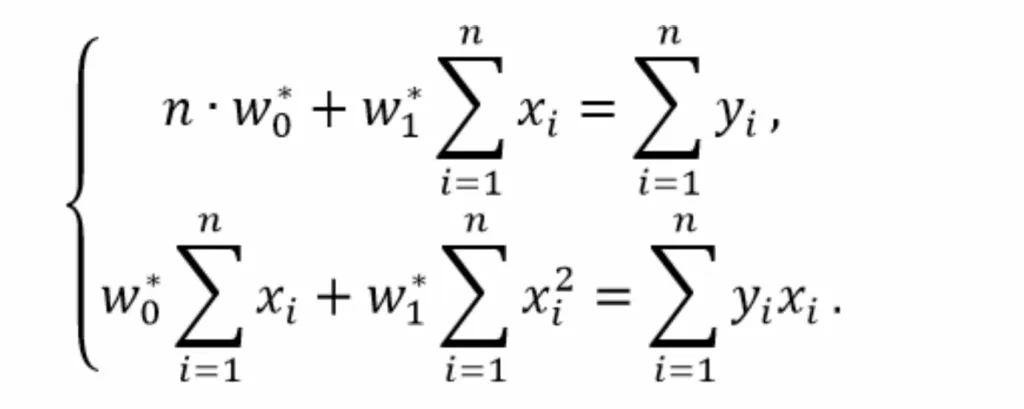
Поставим слагаемые с множителем «x» в левой части в порядке убывания степеней
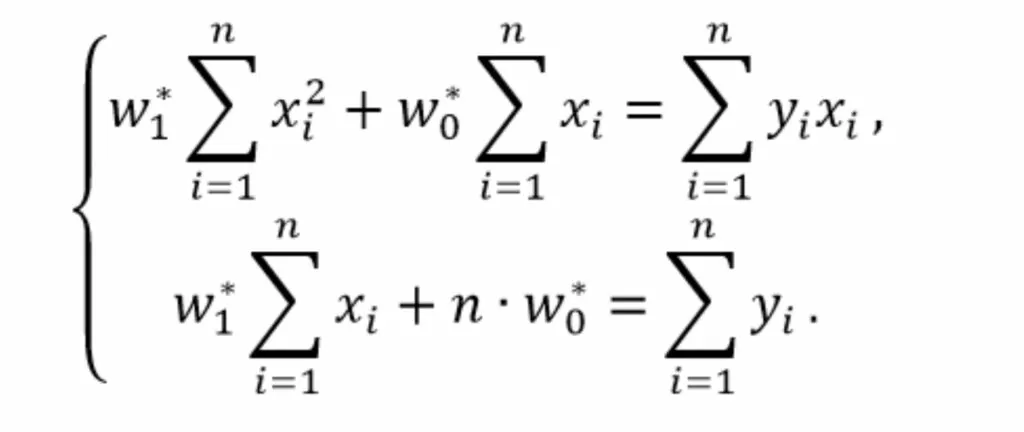
Для решения полученной системы алгебраических уравнения представим её в матричной форме
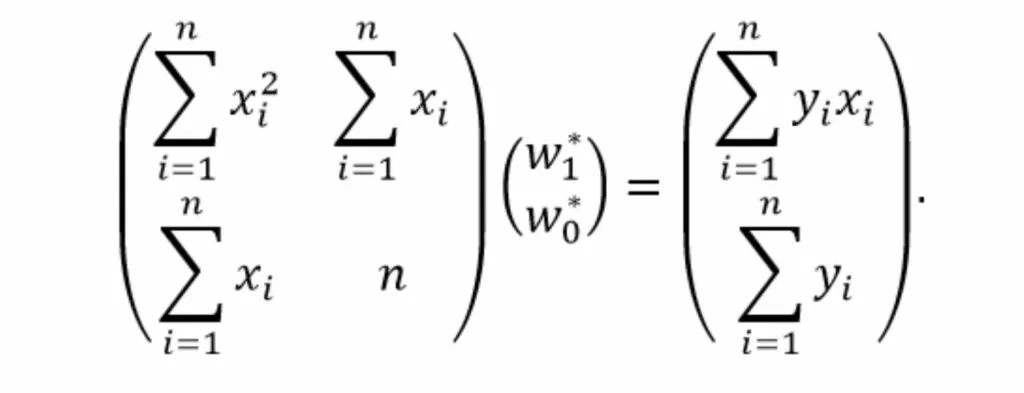
Выразим вектор w* с искомыми весами выполнив умножение обеих частей равенства на обратную матрицу
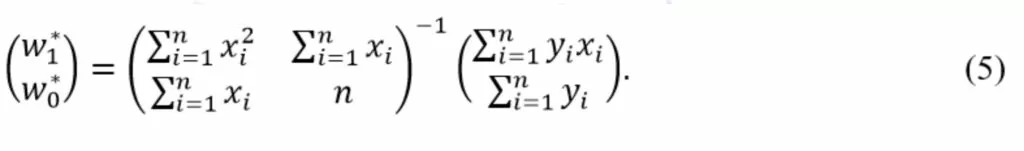
Полученное выражение (5) является решением системы уравнений и его можно уже использовать в качестве первого алгоритма оценки параметров модели. Ниже приведен код реализующий этот алгоритм.
def coefficient_reg_inv(x, y):
size = len(x)
# формируем и заполняем матрицу размерностью 2x2
A = np.empty((2, 2))
A[[0], [0]] = sum((x[i])**2 for i in range(0,size))
A[[0], [1]] = sum(x)
A[[1], [0]] = sum(x)
A[[1], [1]] = size
# находим обратную матрицу
A = np.linalg.inv(A)
# формируем и заполняем матрицу размерностью 2x1
C = np.empty((2, 1))
C[0] = sum((x[i]*y[i]) for i in range(0,size))
C[1] = sum((y[i]) for i in range(0,size))
# умножаем матрицу на вектор
ww = np.dot(A, C)
return ww[1], ww[0]
[w0_1, w1_1] = coefficient_reg_analit(x_scale, y_estimate)
print(w0_1, w1_1)
Результат работы алгоритма:
[33.93193341] [2.01436546]
Выражение (5) можно упростить, выполнив аналитический расчет обратной матрицы.
Найти обратную матрицу можно с использованием, например, алгебраических дополнений. Для пояснения поиска обратной матрицы введем новую переменную A. Пусть

Перепишем выражение (5) в виде
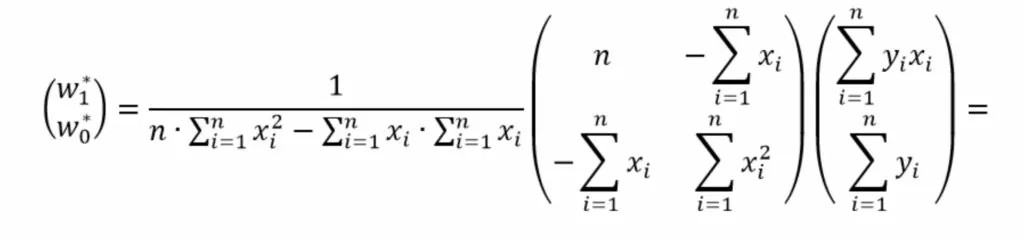
Упростим выражение раскрыв скобки, чтобы получить более компактную форму записи
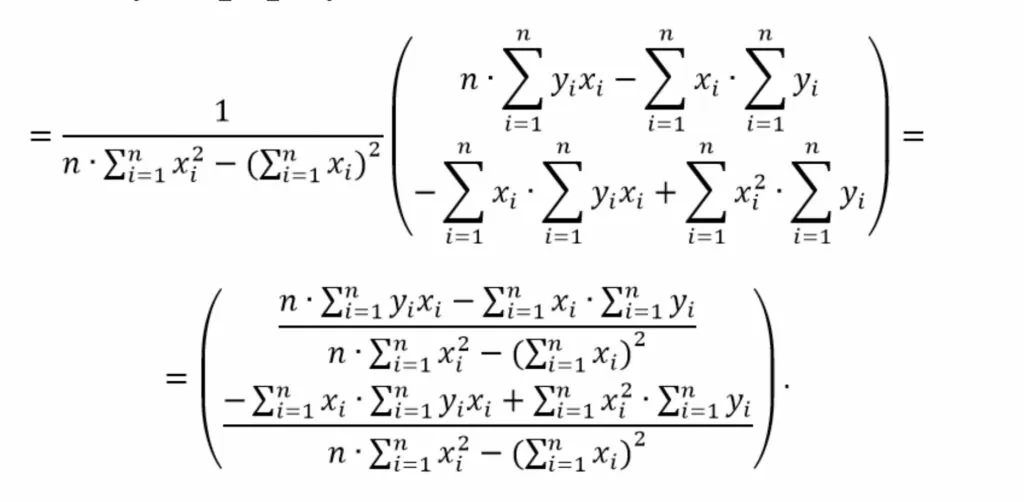
Теперь решение системы уравнений имеет вид
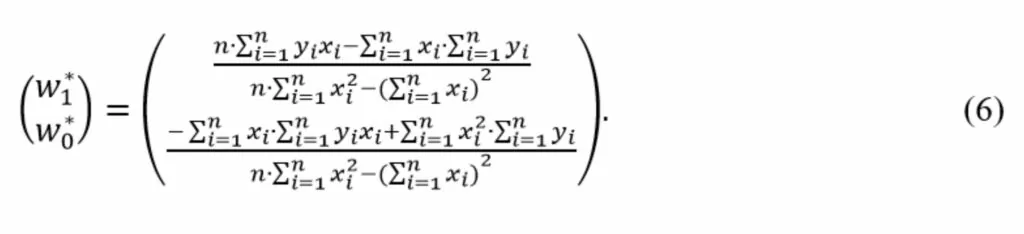
Полученное выражение (6) можно использовать в качестве второго алгоритма оценки параметров модели. Ниже приведен код, реализующий этот алгоритм.
def coefficient_reg_inv_analit(x, y):
size = len(x)
# выполним расчет числителя первого элемента вектора
numerator_w1 = size*sum(x[i]*y[i] for i in range(0,size)) - sum(x)*sum(y)
# выполним расчет знаменателя (одинаковый для обоих элементов вектора)
denominator = size*sum((x[i])**2 for i in range(0,size)) - (sum(x))**2
# выполним расчет числителя второго элемента вектора
numerator_w0 = -sum(x)*sum(x[i]*y[i] for i in range(0,size)) + sum((x[i])**2 for i in range(0,size))*sum(y)
# расчет искомых коэффициентов
w1 = numerator_w1/denominator
w0 = numerator_w0/denominator
return w0, w1
[w0_2, w1_2] = coefficient_reg_inv_analit(x_scale, y_estimate)
print(w0_2, w1_2)
Результат работы алгоритма:
[33.93193341] [2.01436546]
Видно, что полученный результат совпадает с результатом, полученным с использованием выражения (5).
Выполним дальнейшее упрощение полученного выражения (6), чтобы получить более компактную форму записи.
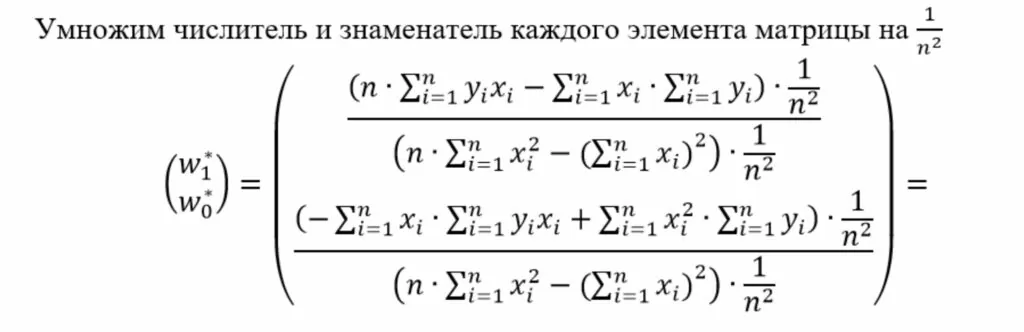
раскроем скобки
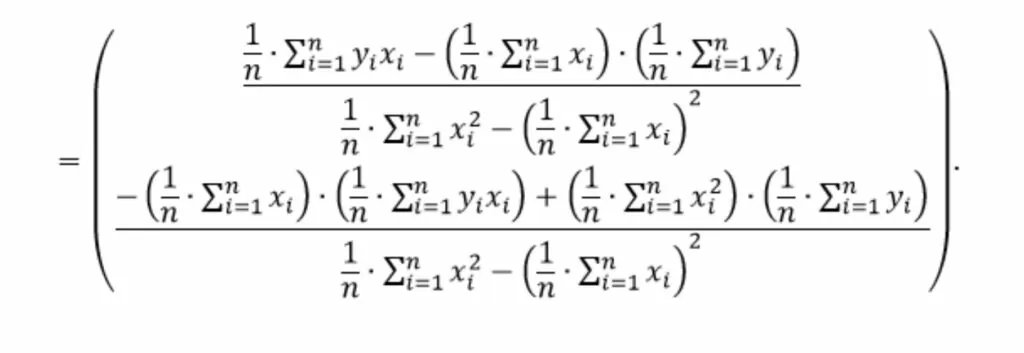
Ведем новые переменные используя термины математической статистики:

С учётом введённых переменных искомый вектор w* примет вид
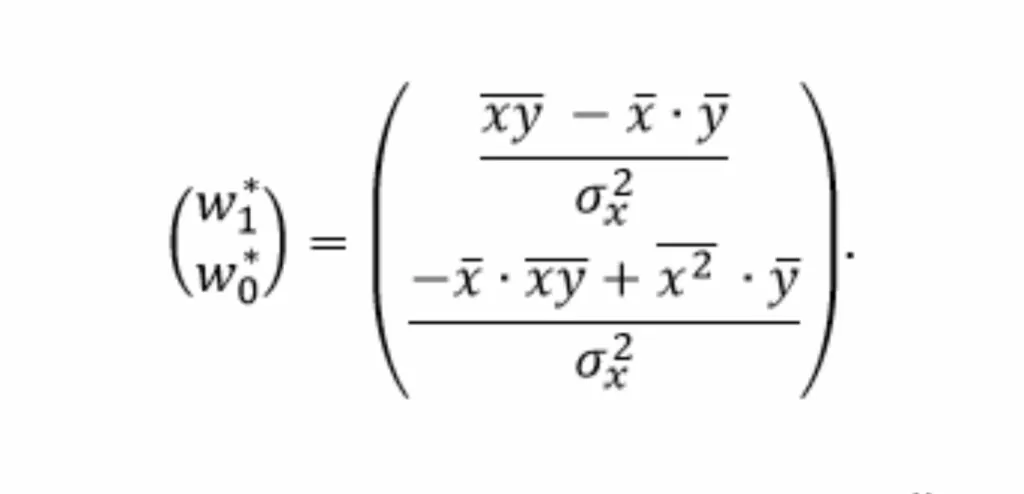

Таким образом итоговое выражение представим в виде

Полученное выражение (7) можно использовать в качестве третьего алгоритма оценки параметров модели. Ниже приведен код, реализующий этот алгоритм.
def coefficient_reg_stat(x, y):
size = len(x)
avg_x = sum(x)/len(x) # оценка МО величины x
avg_y = sum(y)/len(y) # оценка МО величины y
# оценка МО величины x*y
avg_xy = sum(x[i]*y[i] for i in range(0,size))/size
# оценка СКО величины x
std_x = (sum((x[i] - avg_x)**2 for i in range(0,size))/size)**0.5
# оценка СКО величины y
std_y = (sum((y[i] - avg_y)**2 for i in range(0,size))/size)**0.5
# оценка коэффициента корреляции величин x и y
corr_xy = (avg_xy - avg_x*avg_y)/(std_x*std_y)
# расчет искомых коэффициентов
w1 = corr_xy*std_y/std_x
w0 = avg_y - avg_x*w1
return w0, w1
[w0_3, w1_3] = coefficient_reg_stat(x_scale, y_estimate)
print(w0_3, w1_3)
Результат работы алгоритма:
[33.93193341] [2.01436546]
Сравним полученные значения с результатом работы процедуры библиотеки sklearn.
from sklearn.linear_model import LinearRegression
# преобразование размерности массива x_scale для корректной работы model.fit
x_scale = x_scale.reshape((-1,1))
model = LinearRegression()
model.fit(x_scale, y_estimate)
print(model.intercept_, model.coef_)
Результат работы алгоритма:
[33.93193341] [2.01436546]
Видно, что полученный результат полностью совпадает с результатами, полученными ранее.
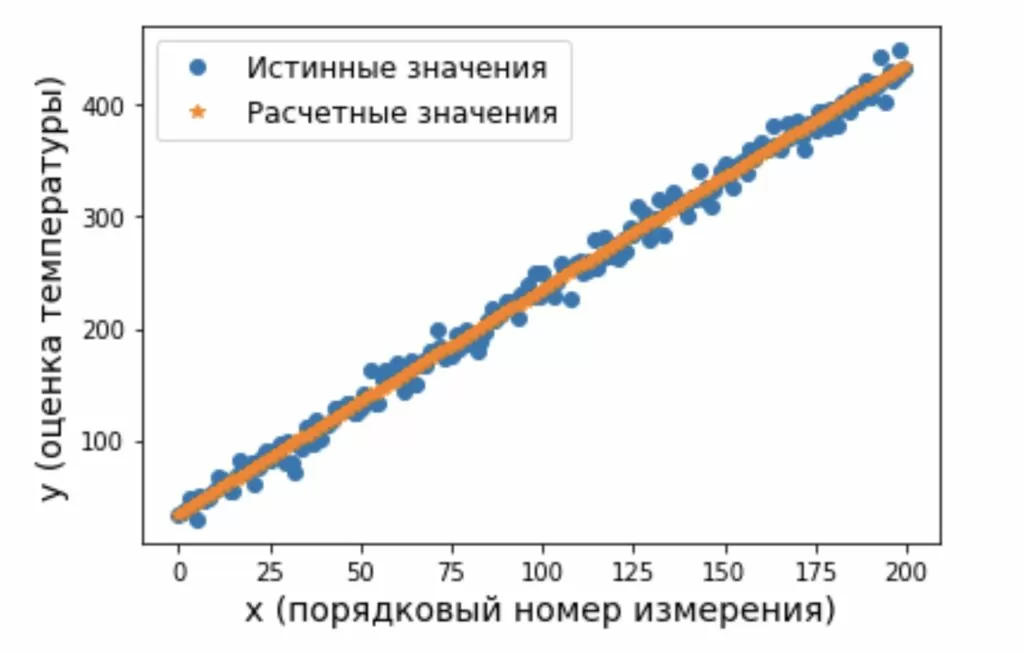
Итак, визуализируем полученный результат, построив прямую с использованием рассчитанных коэффициентов и сопоставим их с исходными данными (рисунок 2).
def predict(w0, w1, x_scale):
y_pred = [w0 + val*w1 for val in x_scale]
return y_pred
y_predict = predict(w0_1, w1_1, x_scale)
plt.plot(x_scale, y_estimate, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_predict, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
Обсуждение алгоритмов
Таким образом удалось выполнить оценку параметров модели, которая описывает процесс изменения температуры в печи с минимальной ошибкой. Выведенные выражения (5) – (7) и запрограммированные по ним три алгоритма, реализующие МНК при обработке одного набора измеренных температур, хотя и отличаются видом конечных выражений, дают одинаковые оценки. Последовательный вывод выражений, выполненный в статье, показывает, что эти выражения по сути «делают» одно и тоже, однако, позволяют давать различные интерпретации. При этом хочется отметить, что в алгоритмах (6) – (7) удалось уйти от процедуры обращения матрицы, которая при обработке реальных данных может выполняться нестабильно.
Ещё один пример. Анализируем остатки.

- количество выбросов в выборке равно 10;
- длительность импульса равна 1-му измерению;
- амплитуда импульса равна 256;
- позиция первого импульса соответствует 10-му измерению;
- период следования импульсов – каждые 20 измерений.
ni = 10 # количество выбросов
ind_impuls = np.arange(ni, data_size, 20) # индексы выбросов
y_estimate_imp = y_estimate.copy() # выборка с выбросами
for i in range(0, ni):
y_estimate_imp[ind_impuls[i]] += 256
[w0_imp, w1_imp] = coefficient_reg_stat(x_scale, y_estimate_imp)
y_pred_imp = predict(w0_imp, w1_imp, x_scale)
plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_imp, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('y (оценка температуры)', fontsize=14)
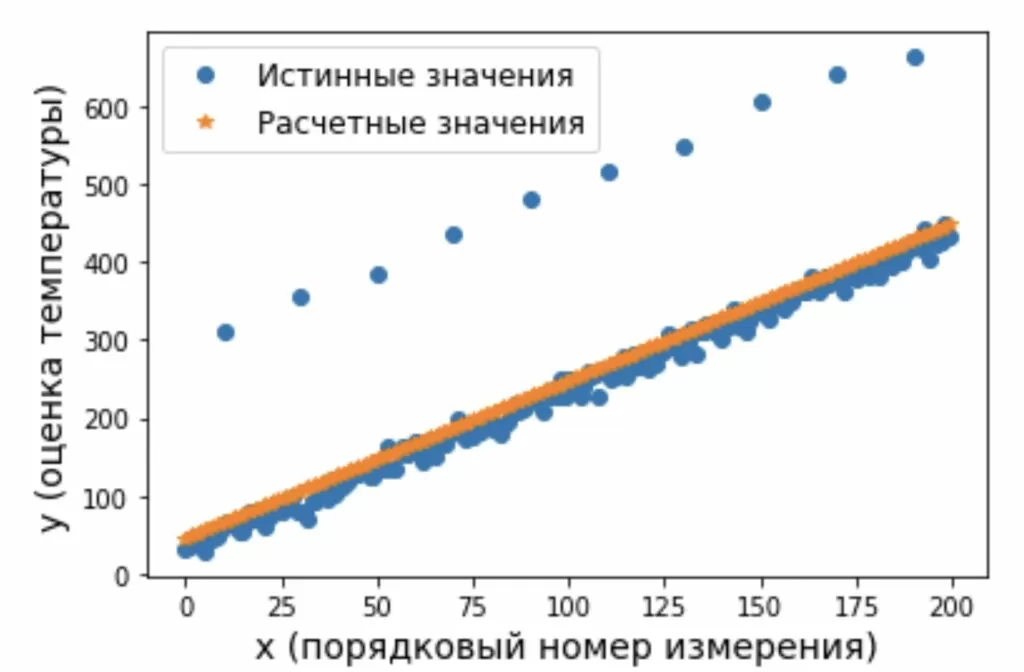
На рисунке 3 видно, что появление выбросов сместило, рассчитанную по выражению (7) прямую в вверх. Модифицируем алгоритм оценки параметров модели за счет новой метрики, а именно оценки квадратов разности между измеренными и модельными данными, которая выполняется по выражению
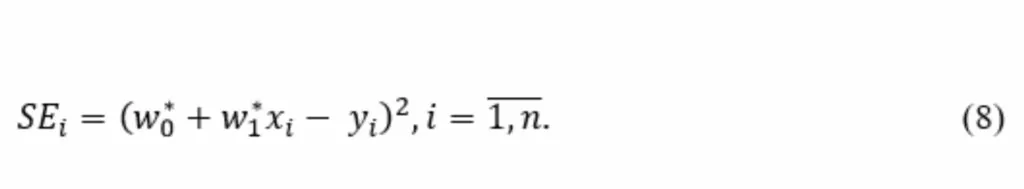
Ниже приведен код, который выполняет этот расчет (8) и визуализирует полученный результат (рисунок 4).
SqErr = (y_pred_imp - y_estimate_imp)**2
plt.plot(x_scale, SqErr, 'o')
plt.xlabel('x (порядковый номер измерения)', fontsize=14)
plt.ylabel('Квадрат ошибки', fontsize=14)
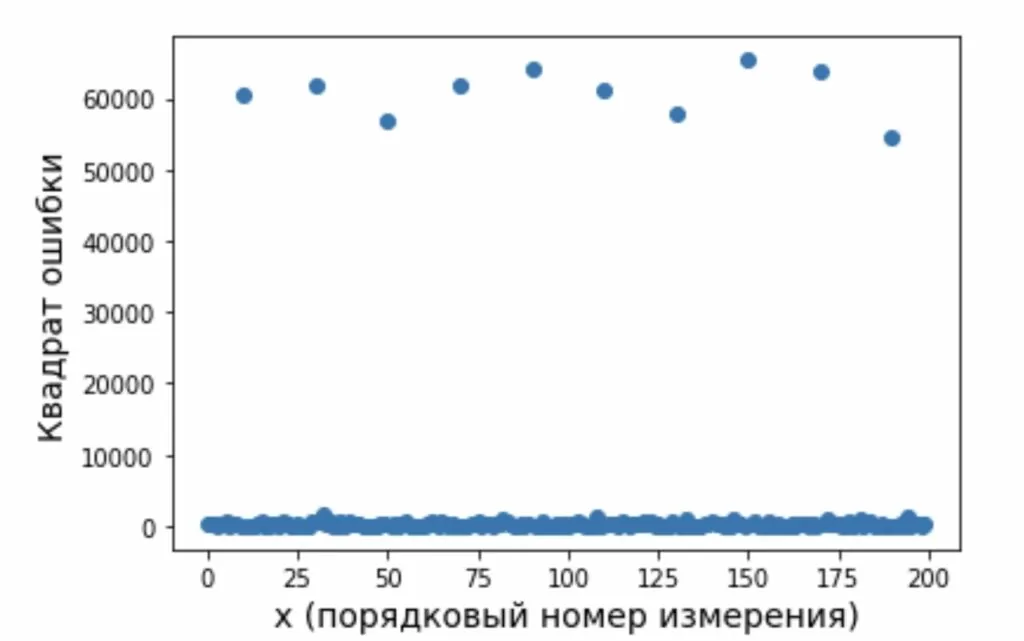
Для устранения влияния помехи на оценки параметров модели, получаемых с использованием алгоритмов, дополнительно введем процедуру цензурирования (отбрасывания) данных, которые имеют большое значение квадрата ошибки (8). С новыми начальными условиями алгоритм оценки параметров модели теперь дополняется следующей последовательностью действий

def censor_data(SqErr, nCensor):
# индексы отсортированного во возрастанию массива с квадратами ошибок
I = np.argsort(SqErr[:,0])
ind_imp = I[-nCensor:]
ind_imp = ind_imp[::-1] # разворот индексов массива
w0 = np.empty((nCensor, 1))
w1 = np.empty((nCensor, 1))
for i in range(0,nCensor):
# цензурирование данных
x_scale_cens = np.delete(x_scale, ind_imp[0:i], 0)
y_estimate_imp_cens = np.delete(y_estimate_imp, ind_imp[0:i], 0)
# расчёт параметров модельной прямой
w0[i], w1[i] = coefficient_reg_stat(x_scale_cens, y_estimate_imp_cens)
y_pred2_cens = predict(w0[i], w1[i], x_scale_cens)
return w0, w1
nCensor = 20 # количество отбрасываемых выбросов
[w0_с, w1_с] = censor_data(SqErr, nCensor)
plt.plot(coef_true[0], coef_true[1], 'o', label = 'Истинные значения')
plt.plot(w0_с, w1_с, '-*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlim((30, 50))
plt.ylim((1.85, 2.15))
plt.xlabel('w0', fontsize=18)
plt.ylabel('w1', fontsize=18)
По итогам работы алгоритма построим полученные оценки параметров модели (рисунок 5) по мере цензурирования данных.
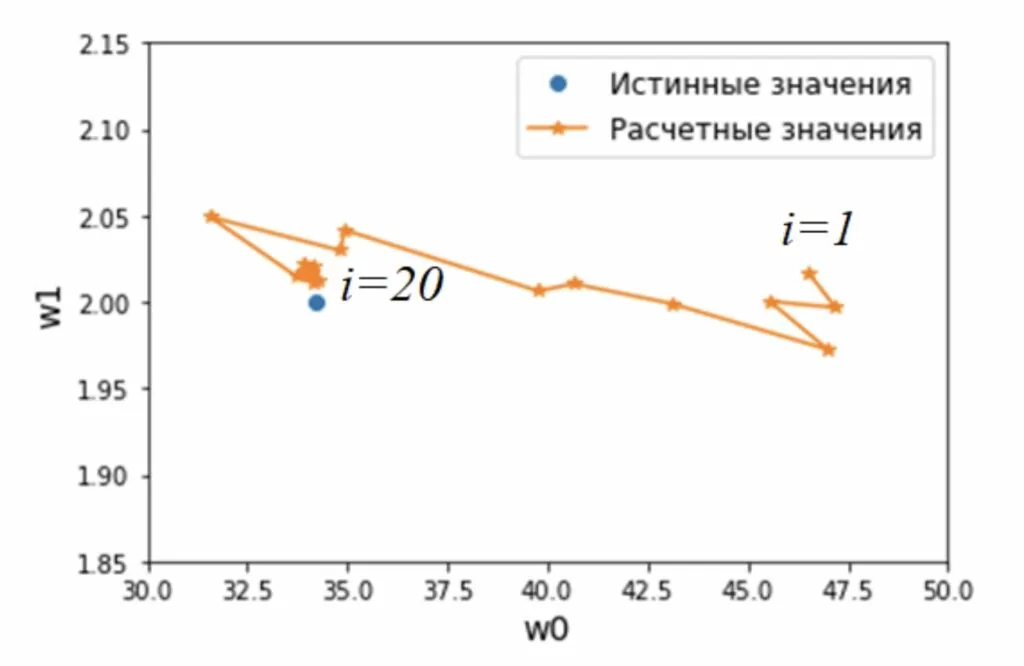
В результате работы рассматриваемого алгоритма видно (рисунок 5), что по мере цензурирования помеховых данных параметры модели приближаются к истинным (точка с оценкой параметров возле i=1 получена после удаления первой точки, точка с оценкой параметров возле i=20 получена после удаления двадцатой точки).
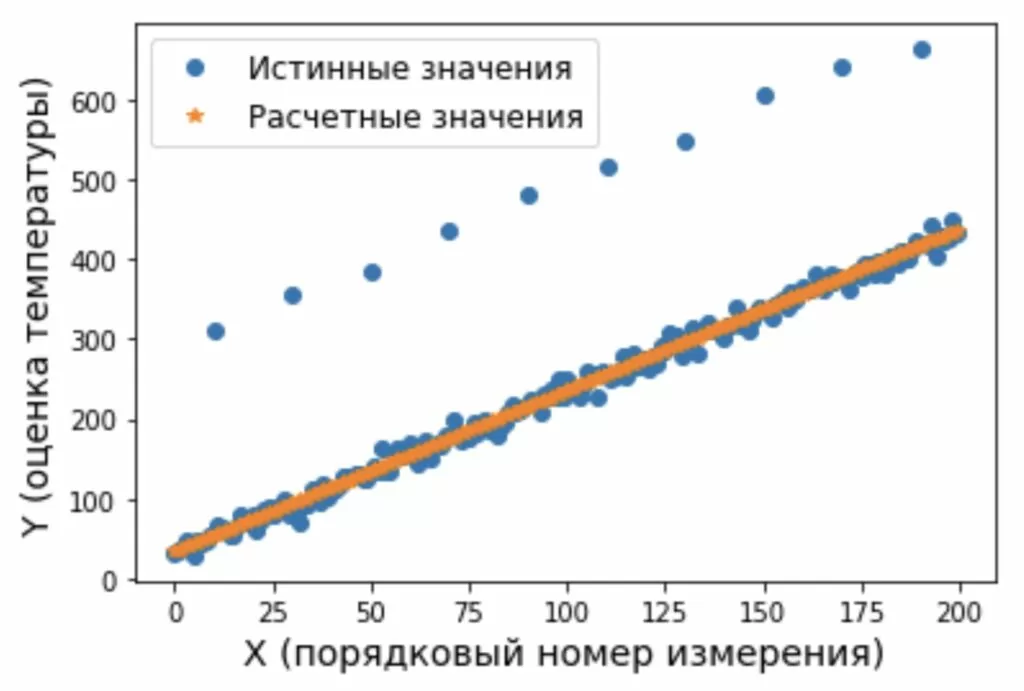
Ниже приведен код, который рассчитывает и строит на графике прямую (рисунок 6) с использованием параметров модели, полученной на последнем шаге алгоритма c цензурированием. На этом рисунке видно, что использование дополнительной процедуры цензурирования данных на основе анализа остаточной суммы квадратов, позволяет улучшить согласование оцениваемых параметров с истинными.
y_pred_censor = predict(w0_с[nCensor-1], w1_с[nCensor-1], x_scale)
plt.plot(x_scale, y_estimate_imp, 'o', label = 'Истинные значения')
plt.plot(x_scale, y_pred_censor, '*', label = 'Расчетные значения')
plt.legend(loc = 'best', fontsize=12)
plt.xlabel('X (порядковый номер измерения)', fontsize=14)
plt.ylabel('Y (оценка температуры)', fontsize=14)
Обсуждение алгоритма
Был рассмотрен алгоритм оценки параметров модели, которая описывает процесс изменения температуры в печи при наличии помех в измерениях. Показано, как зная логику построения алгоритма его можно модифицировать под изменившиеся условия и получить необходимый результат (оценку параметров модели).
Безусловно, что приведенный в статье алгоритм оценки параметров модели с использованием процедуры цензурирования импульсных помеховых сигналов (в том виде, в котором он приведен в статье) не является оптимальным и универсальным. Он приведен здесь для иллюстрации возможностей модификации алгоритма, реализующего классический МНК. А также для демонстрации ещё одной важной метрики при использовании МНК – оценка квадратов разности между измеренными и модельными данными (8), которая является источником множества различных модификаций метода.
Заключение
В статье делается попытка «расколдовать» классический МНК, а также продемонстрировать удобство методологической интерпретации решения задачи в виде триады «модель-алгоритм-программа», которая позволяет осуществить бесшовный переход от модельной постановки задачи и задания начальных условий до её программной реализации. Ставилась задача в максимально доступной для читателя форме продемонстрировать последовательность математической мысли при решении задачи с применением МНК. Показать, как начальные условия влияют на полученные конечные выражения. Автор надеется, что статья будет полезной для всех тех, кто при решении различных задач анализа данных попытается применить или модифицировать классические методы и для этого попробует также с «карандашом в руках» выполнить вывод конечных выражений. Этот подход позволит разработчику применять на практике понятные для него алгоритмы, а не код, который работает «по неведомым» правилам.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)