Время прочтения: 6 мин.
Временные ряды и бизнес
Большое количество современных данных имеют временную структуру. Такой структурой, например, обладают экономические и финансовые переменные (ВВП, инфляция, цены акций), продажи и другие. Многим компаниям необходимо планирование, поэтому прогнозирование с помощью моделей временных рядов является неотъемлемой частью анализа данных в бизнесе. Интерес к этой теме заметен и по количеству инструментов, которое выпускается компаниями. Модель Orbit, про которую я расскажу была создана в компании Uber, её предшественником был Prophet. Обе модели были выпущены в виде Python-библиотек для открытого использования.
Модели экспоненциального сглаживания
Классическим для временных рядов является прогнозирование с помощью моделей вида ARIMA(p, d, q), которые учитывают p предыдущих периодов в качестве регрессоров для текущего. Альтернативная ветвь развития, которая получила достаточно большое внимание в последнее время – модель экспоненциального сглаживания. В этом методе в прогноз входит значение переменной за все предыдущие периоды, однако вес предыдущих периодов экспоненциально снижается по мере удаления от прогнозируемого периода. В простой форме экспоненциальное сглаживание может быть записано как:
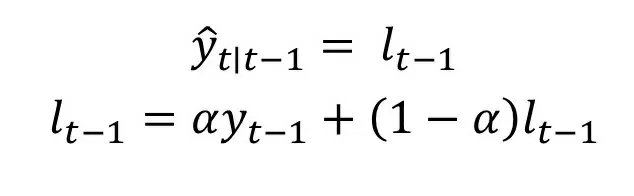
Такая формулировка модели является максимально простой, поэтому плохо работает, когда в данных есть тренд или сезонность. В базовую модель обычно добавляют следующие компоненты: E (Error, ошибка), T (Trend, тренд), S (Seasonality, сезонность). Эти дополнения могут включаться в модель аддитивно (A), мультипликативно (M) и отсутствовать (N). Из-за таких сокращений модели экспоненциального сглаживания обычно записываются как ETS(X, X, X) – где вместо X стоят A, M или N в зависимости от того, как соответствующая компонента включается в модель. Наиболее распространенным видом модели является модель Холта-Винтерса ETS(A, A, A). Прогноз модели в ней задается как:
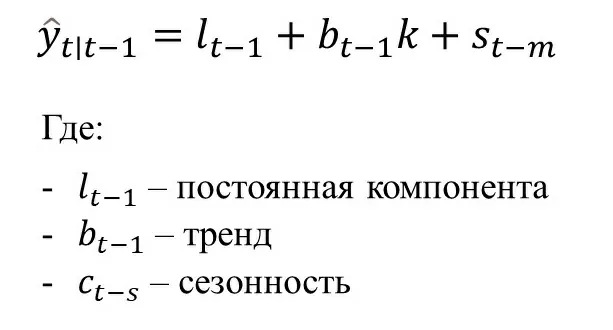
Расчет переменных происходит по следующим формулам:
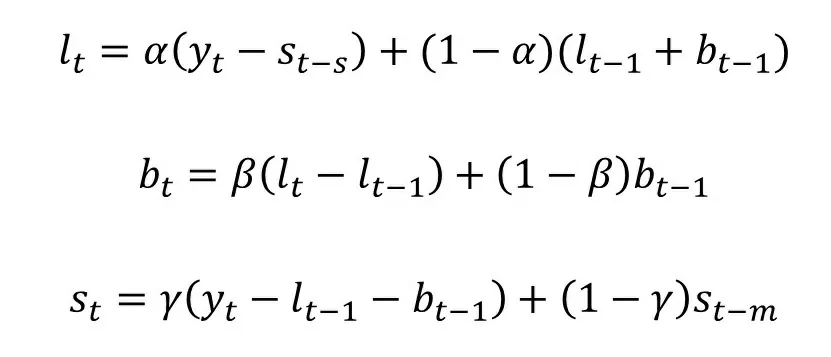
Orbit
Авторы статьи Orbit приводят расширенную версию модели экспоненциального сглаживания. Они предлагают две вариации модели – LGT (Local and Global Trend) и DLT (Damped Local Trend).
LGT
Модель LGT формулируется следующим образом:
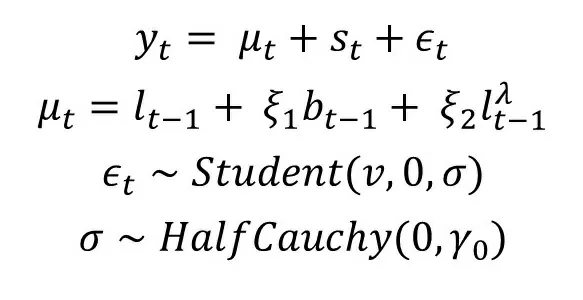
Все параметры зависят от предыдущих значений следующим образом:
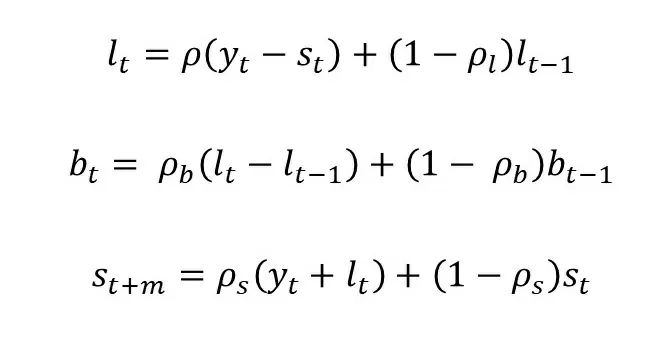
В данном уравнении добавляются незнакомые нам переменные – b, которая отвечает за тренд и s, которая отвечает за сезонность и смотрит на соответствующее значение m периодов назад. В процессе обучения модели происходит подбор параметров ρ, ξ, λ, ν.
у₀ является параметром нормировки, который определяется по данным. Для подбора параметров используются Байесовские методы (например, один из вариантов подбора параметров – Метод Монте-Карло Марковских Цепей).
DLT
Процесс предсказания целевой переменной формулируется следующим образом:
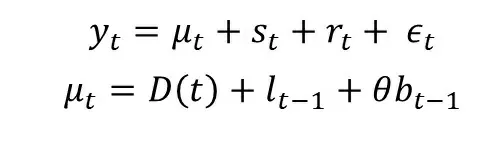
Процесс обновления параметров по прошлым значениям записывается как:
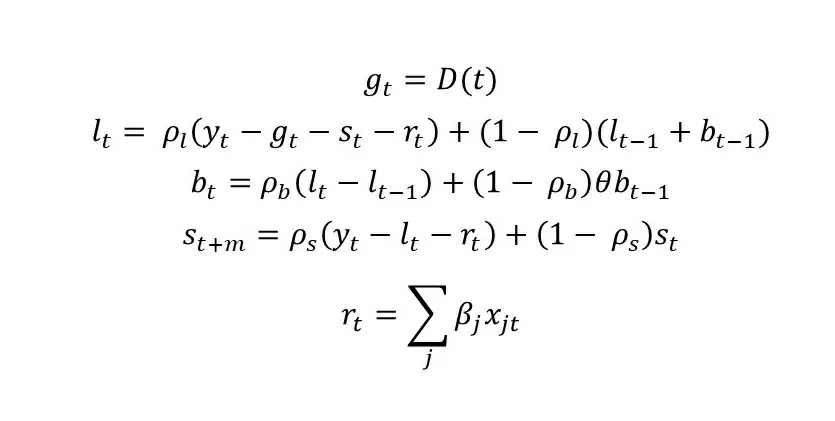
Отличие данной модели заключается в том, что в нее включатся регрессоры rt. Веса регрессоров инициализируются стандартным нормальным распределением и потом подбираются во время оптимизации. Тренд D(t) является детерминистическим (не выражен случайной функцией) и может задаваться в линейном, лог-линейном и логистическом виде.
Применение в Python
Для работы в Python можно воспользоваться готовой реализацией алгоритма Orbit. Библиотека устанавливается с помощью команды
pip install orbit-mlБиблиотека содержит собственный набор данных, который я буду использовать для демонстрации. Посмотрим на данные:
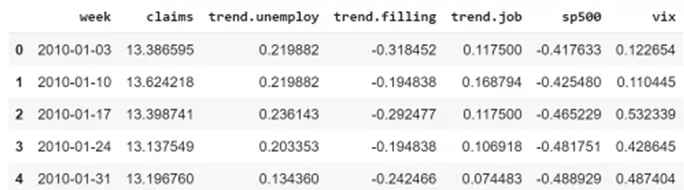
Данные содержат несколько переменных. Буду предсказывать переменную claims – количество заявок на пособие по безработице, зарегистрированных за неделю в США. Дополнительно, набор данных содержит вида trend. – это значение из сервиса Google Trends. Оно показывает, насколько популярны слова – unemploy, filling, job. Две последние переменные являются фондовыми индексами.
Разведочный анализ данных
Проведем разведочный анализ данных.
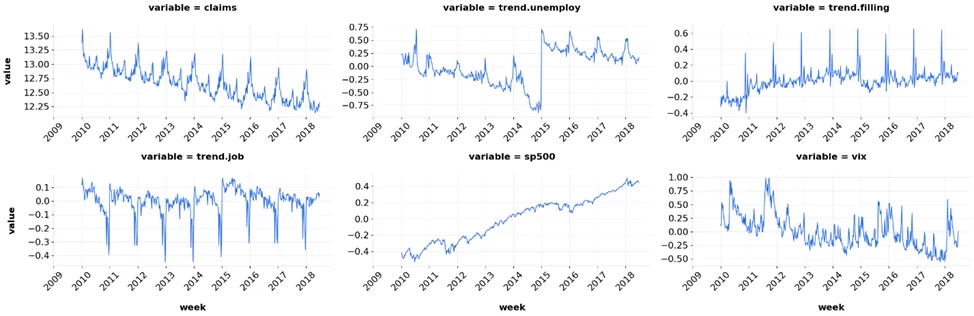
Библиотека позволяет построить графики всех переменных. В функцию необходимо передать переменную с датафреймом (data), колонку с датами (“week”) и массив с названиями переменных, которые мы хотим построить.
from orbit.eda.eda_plot import wrap_plot_ts
wrap_plot_ts(data, "week", list(data.columns))
Дополнительно, можно построить две переменные на одном графике. Построим claims и trend.filling. В функцию необходимо передать набор данных (df), колонку с датой (date_col), и переменные, которые мы хотим построить (var1, var2)
from orbit.eda.eda_plot import dual_axis_ts_plot
_ = dual_axis_ts_plot(df=data, var1="claims", var2="trend.filling", date_col="week")
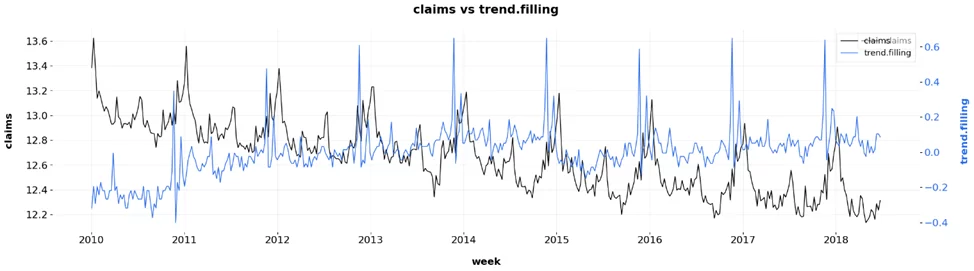
Здесь можно увидеть, что пики trend.filling в большом количестве случаев обгоняют пики claims. Этот признак может быть информативен в качестве регрессора.
Построение модели
Перед построением моделей выделю последние 52 недели в тестовую выборку.
DLT
from orbit.models import DLT
dlt = DLT(
response_col="claims",
date_col="week",
regressor_col=["trend.filling", "trend.job", "trend.unemploy"],
seasonality=52
)
dlt.fit(df=train_data)
Сначала инициализирую модель. Передаю в класс название колонки с целевой переменной (response_col), название колонки с датами (date_col), массив с названиями колонок регрессоров (regressor_col) и сезонность. В данном случае, я выбрал сезонность равную 1 году – 52 недели. Далее, вызываю метод fit для обучения модели на обучающей выборке.
После обучения модели можно предсказать тестовые данные и визуализировать предсказание.
from orbit.diagnostics.plot import plot_predicted_data
predicted_data = dlt.predict(df=test_data)
plot_predicted_data(training_actual_df = train_data,
predicted_df = predicted_data,
date_col = dlt.date_col,
actual_col = dlt.response_col,
test_actual_df = test_data)
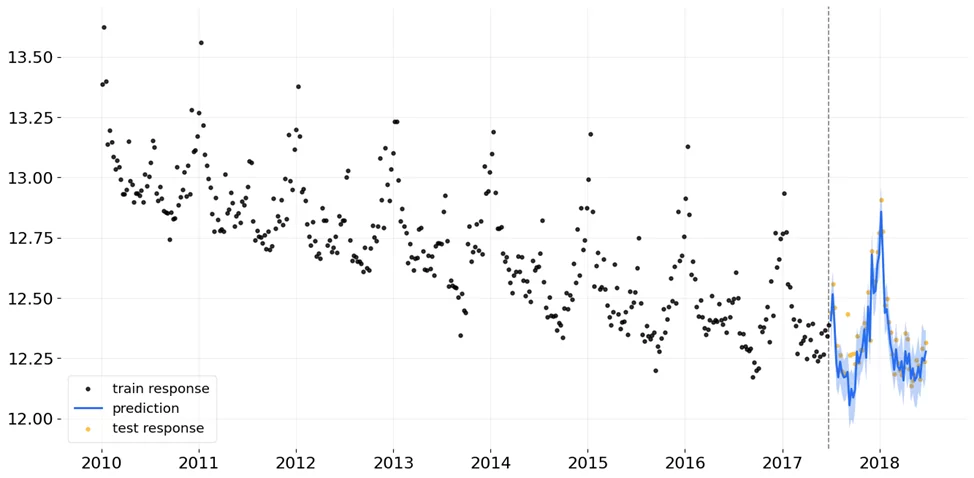
Для визуализации предсказания необходимо передать в функцию обучающий набор данных, предсказанные значения, название колонки с датами, название колонки с целевой переменной и тестовый набор данных. Как было указано выше, в этой модели могут быть использованы разные виды тренда, тип тренда может быть передан в параметре global_trend_option. Выбор типа тренда повлияет на предсказания модели.
Далее можно посмотреть на поведение отдельных компонентов модели.
from orbit.diagnostics.plot import plot_predicted_components
predicted_data = dlt.predict(data, decompose=True)
plot_predicted_components(predicted_data, "week")
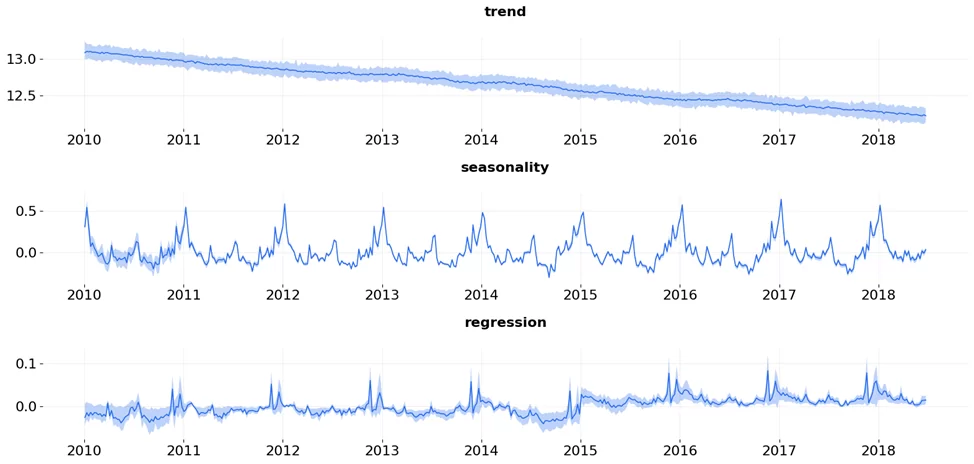
LGT
Работа с LGT моделью производится с помощью тех же функций. Отличается только шаг с определением модели – LGT не имеет регрессоров.
Сравнение моделей
После того, как получены предсказания моделей на тестовых данных, можно сравнить их качество для предсказания. В качестве дополнительного бенчмарка также взята классическая модель ARIMA (реализация auto_arima из библиотеки pmdarima). Результаты моделей представлены в таблице:
| Модель | MSE |
| LGT | 0.0049 |
| DLT | 0.0059 |
| ARIMA | 0.032 |
Таким образом, модели экспоненциального сглаживания показали себя лучше, чем классическая модель ARIMA.
Несмотря на то, что в сфере моделирования временных рядов ARIMA-модели являются наиболее популярными, заинтересованность крупных компаний в данных с временной структурой приводит к развитию новых методов, которые могут превосходить качество классических моделей. При текущей скорости инноваций в данной области, можно предположить, что развитие Orbit не заставит себя ждать. За счет этого можно надеяться на ускоренное развитие этой, казалось бы, консервативной сферы анализа данных.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
