Время прочтения: 4 мин.
Предположим, перед аналитиком стоит задача исследовать информацию о количестве людей на сайте в определенное время в определенный день, имея выборку по посещению сайта за несколько месяцев каждые 30 минут. И сделать прогноз посещения на будущий период.
Данные по посещниям представлены на графике ниже
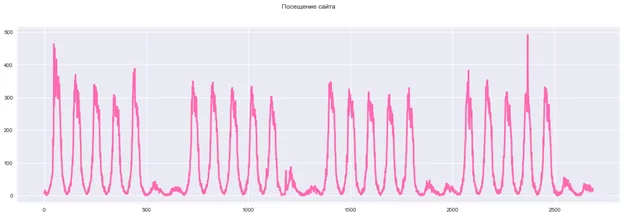
Как видно из графика, характер данных имеет явную периодическую составляющую. Разложим наши данные в ряд Фурье по следующей формуле.
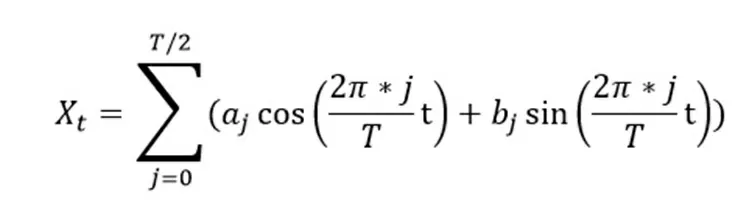
Ниже представлена функция, которая принимает в качестве аргумента датафрейм с исходными данными. Эта функция использует только самые простые библиотеки, чтобы мы могли использовать декоратор компиляции. Расчет при большом объёме данных может занять значительное время, а компилятор ускоряет скорость расчета в 100 раз.
@numba.jit (nopython = True)
def period(df['SA']):
a , b = [] , []
a.append(dfv.mean())
b.append(0)
for i in range(1 , len(dfv)//2 + 1):
p = 0
q = 0
for j in range(1, len(dfv)+1):
p = p + dfv[j - 1] * math.cos(2 * math.pi * i * j / len(dfv))
q = q + dfv[j - 1] * math.sin(2 * math.pi * i * j / len(dfv))
a.append(2 / len(dfv) * p)
b.append(2 / len(dfv) * q)
gramma = []
for i in range(len(a)):
k = (a[i] ** 2 + b[i] ** 2) * len(dfv) / 2
gramma.append( k )
return a, b, gramma
Результатом работы этой функции являются три списка, два с коэффициентами a и b из формулы выше для разложения в ряд Фурье и один с квадратами амплитуды для построения графика периодограммы.
Ниже на графике представлены две кривые, одна — реальные данные, другая — это прогноз, использующий разложения данных в ряд Фурье с учетом всех гармонических составляющих (N/2), где N — число наблюдений. Как мы можем видеть, прогноз полностью совпадает с реальными данными.
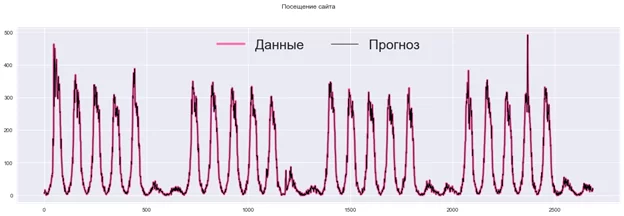
Для определения наиболее значащих гармоник необходимо построить периодограмму. По оси х — это порядковый номер гармоники от 0 до Т/2, по оси Y — значение квадратов амплитуды, полученных из функции выше.
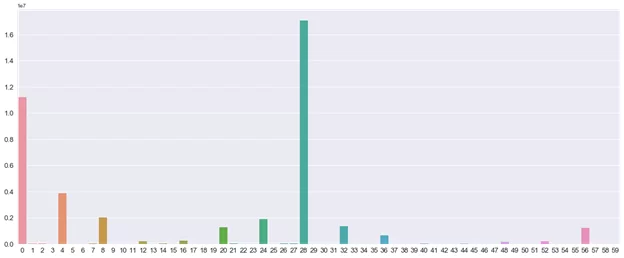
Полученный график периодограммы показывает какие гармоники являются наиболее значимыми, то есть оказывают наибольшее влияние на значение функции.
Для прогнозирования и анализа данных нам нужны только гармоники с высокой амплитудой, иначе нельзя будет использовать для прогнозирования, так как это приведёт к переобучению модели – точному соответствию тренировочной выборке и слабому результату на тестовой.
Реализовать выбор гармоник с самой высокой амплитудой можно следующим образом:
zn = [0,4,8,20,24,28]
for i in range(len(a)):
if i not in zn:
a[i] , b[i] = 0,0
prog = []
for i in range(1 , len(df) + 1):
r = 0
for j in range(len(a)):
r = r + a[j] * cos(2 * pi * j * i/len(df)) + b[j] * sin(2 * pi * j * i/len(df))
prog.append(r)
y1 = df['SA']
y2 = prog
fig , ax = plt.subplots()
plt.plot(x, y1 , c = 'hotpink' , linewidth = 4 ,label ='Данные')
plt.plot(x, y2, c = 'Black', linewidth = 3,label ='Прогноз')
ax.legend(loc = 'upper center' , fontsize = 25 , ncol = 2 )
fig.set_figwidth(20)
fig.set_figheight(6)
fig.suptitle("Посещение сайта")
plt.show()
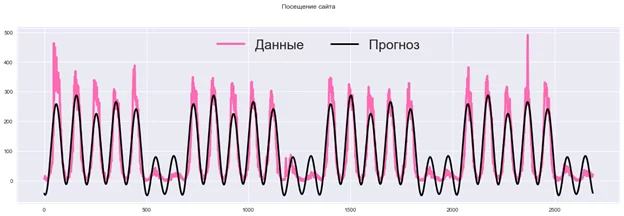
Как видно из графика выше, применение описанного метода позволяет получить очень хороший прогноз с использованием всего шести наиболее значимых гармоник. В нашем примере это 0,4% от всех 1344 гармоник.
Таким образом, результатом применения описанного метода является новая независимая переменная, позволяющая существенно улучшить прогноз.
Конечно, не все исходные данные будут иметь такую явную периодическую составляющую как в этом примере, но тем и хорош спектральный анализ, что он позволяет выявлять даже неочевидные или скрытые периодические закономерности.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)