Время прочтения: 6 мин.
В данном посте я разберу задачу причинно-следственного (Causal Inference) и затрону отдельные аспекты её решения с помощью ациклических направленных графов с использованием инструментов языка программирования R, не погружаясь в сложную математическую терминологию.
Ациклических направленный граф (Directed Acyclic Graph) или сокращенно DAG – это однонаправленный граф, в котором отсутствуют циклы. Данный инструмент хорошо подходит к решению задач причинно-следственного вывода, так как граф является удобным средством визуализации взаимосвязей между объектами или явлениями.
В рамках задачи каждое ребро графа будет представлять собой причинно-следственную связь между соответствующими вершинами и в графе будут отсутствовать пути, ведущие от любой вершины к ней же самой.
Теперь рассмотрю пакет dagittyязыка R для работы с ациклическими направленными графами и ggdag – пакет, ориентированный на гибкую отрисовку графов, основанный на упомянутом ранее dagitty и графических пакетах ggplot2 и ggraph.
Рассмотрю основные методы для построения графа (DAG) и анализа взаимосвязей между вершинами. В начале подключу данные библиотеки.
library(dagitty)
library(ggdag)
Для определения графа используется текстовый синтаксис (см. код далее).
gdag <- dagitty("dag{A->B;A->C;A->E;B->D;C->D;D->E}")В примере выше я определил граф в рамках отношения причинно-следственной связи каждой из вершин графа, но можно сделать более кратко, определив отношения вершины с набором других вершин.
gdag <- dagitty("dag {A->{B C E};B->D;C->D;D->E}")Ключевое слово dag необходимо, т.к. dagitty работает с несколькими разновидностями графов.
Далее выведу изображение самого графа (Граф 1). Это можно сделать с помощью метода graphLayout, который автоматом строит макет графа, но я задам координаты самостоятельно и воспользуюсь пакетом ggdag для построения графа.
coordinates(gdag) <- list (
x=c(A=2, B=1, C=3, D=2, E=3),
y=c(A=5, B=4, C=4, D=3, E=2))
tidy_dag <- tidy_dagitty(gdag)
ggdag(tidy_dag) +
theme_dag()
Получу следующий результат:
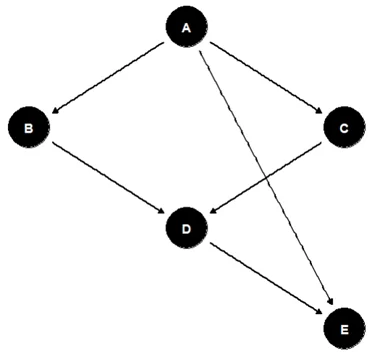
Граф 1
Dagitty содержит методы для определения отношений между вершинами графа: parents – родители, ancestors — предки, children — дети, descendants – потомки. Найду всех родителей, предков, детей и потомков вершины (переменной) D:
parents(gdag, "D")
[1] "A" "B" "C"
ancestors(gdag, "D")
[1] "D" "C" "B" "A"
children(gdag, "D")
[1] "E"
descendants(gdag, "D")
[1] "D" "E"
Теперь обозначу на графе все родительские вершины графа по отношению к «D»
ggdag_parents(gdag, "D") + theme_dag_blank()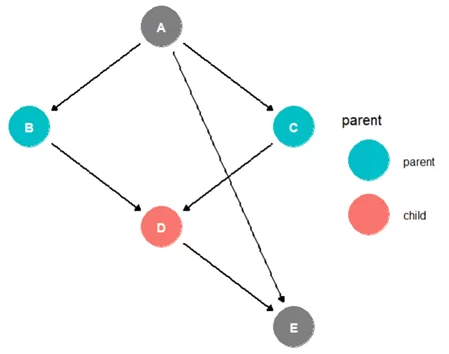
В качестве родительских вершин для D обозначены B и C. Такая вершина с более чем одним родителем называется коллайдером (collider).
Аналогично выведу все дочерние вершины графа для вершины «D».
ggdag_children(gdag, "D") + theme_dag_blank()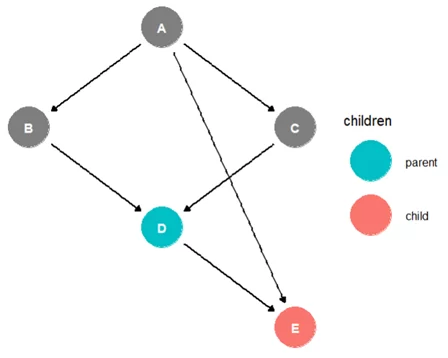
Как видно на графе, единственной дочерней вершиной для D является E.
В графе между двумя вершинами могут существовать альтернативные пути.
Найду все возможные пути в графе между вершинами A и E помощью метода paths.
paths(gdag, "A", "E")
$paths
[1] "A -> B -> D -> E" "A -> C -> D -> E" "A -> E"
$open
[1] TRUE TRUE TRUE
Или можно воспользоваться методом ggdag_paths пакета ggdag. Задам A как причину (exposure) и E как результат (outcome).
exposures(gdag) <- c("A")
outcomes(gdag) <- c("E")
ggdag_paths(gdag)
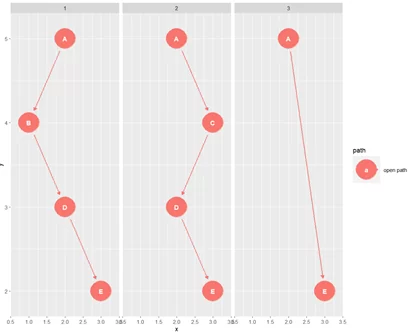
В качестве результата видим 3 пути от вершины A до E. Метод является полезным для поиска «обходных» путей.
Теперь изображу граф (Граф 2) в котором есть причинно-следственная связь B->C и некий фактор (переменная) A, который оказывает влияние и на причину (B) и на результат (С). Такая переменная называется confounder. Подобные переменные в ходе анализа необходимо учитывать, т.к. их влияние может искажать исследование, либо вообще говорить о ложности предположения о причинно-следственной связи.
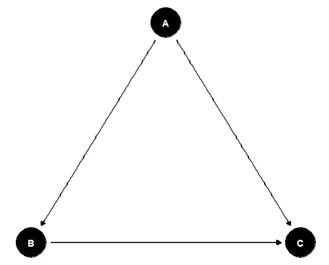
Граф 2
Теперь представлю, что нужно провести исследование, в котором максимально точно определить эффект D->E (Граф 1). В ходе чего мне необходимо найти минимальный набор вершин (adjustment set), которые могут влиять на результат анализа взаимосвязи причины (exposure) — D и результата (outcome) – E для дальнейшего учета их влияния и получения более точных результатов. В качестве примера можно привести исследование, посвященное влиянию диеты на общее состояние здоровья, где в подобный набор вершин скорее всего войдут такие факторы как возраст, вес, уровень физической активности, которые могут повлиять на результат исследования.
Однако вернусь к примеру:
exposures(gdag) <- c("D")
outcomes(gdag) <- c("E")
tidy_dag <- tidy_dagitty(gdag)
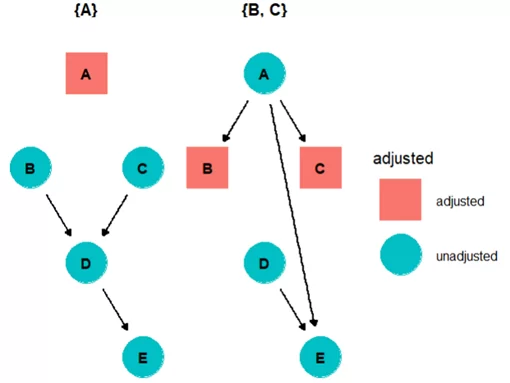
ggdag_adjustment_set(tidy_dag, node_size = 14, text_col = "black") +
theme_dag()
В качестве результата получу два варианта – вершина A и вершины B и С.
Теперь перейду в более наглядному примеру и рассмотрю причинно-следственную связь между присутствием бобров и возникновением плотины на реке. Задам в комплексе набор факторов и построю граф (DAG). Для этого воспользуюсь методом dagify пакета ggdag. Здесь при задании отношений использую символ ‘~’, например, dam ~ beavers означает, что присутствие бобров является причиной построения плотины. В качестве причины (exposure) задам вершину обозначающую присутствие бобров (beavers), а в качестве результата (outcome) – бобровую плотину (dam). Уровень реки (river) и количество деревьев (trees) будут являться причиной и для присутствия бобров (beavers), и для построения плотины (dam).
beaver_effect_dag = dagify(
beavers ~ river,
beavers ~ trees,
dam ~ river,
dam ~ beavers,
dam ~ trees,
exposure = 'beavers',
outcome = 'dam')
beaver_effect_dag%>%ggdag(node_size = 22) +
theme_dag()
Получу следующий граф:
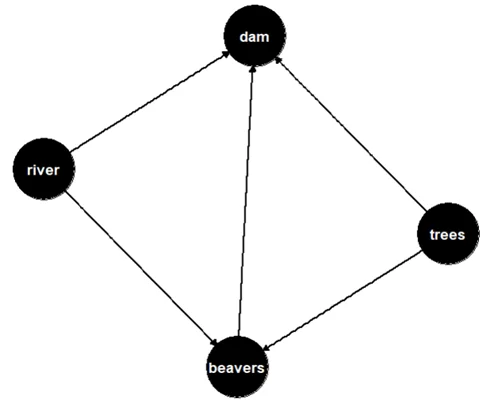
Граф 3
Определю минимальный набор вершин для оценки эффекта beavers->dam
tidy_dag <- tidy_dagitty(beaver_effect_dag)
ggdag_adjustment_set(tidy_dag, node_size = 19, text_col = "black") +
theme_dag()
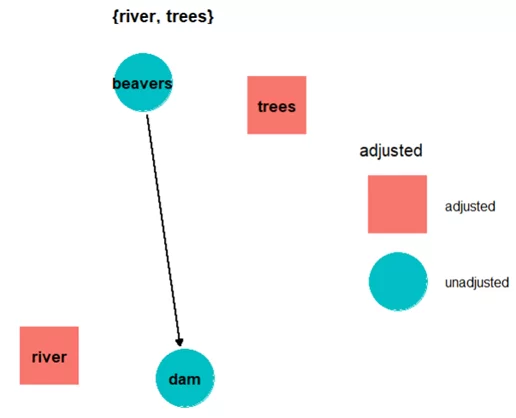
В качестве результата получу множество из вершин уровень реки (river) и количество деревьев (trees). Их необходимо учитывать в ходе дальнейшего анализа взаимосвязи присутствия бобров и возникновения плотины на реке.
В заключение хотелось бы подчеркнуть: несмотря на то, что DAG довольно прост для восприятия, при этом имеет строгую математическую основу. Основное преимущество ациклических направленных графов (DAG) заключается в возможности явного изложения причинно-следственных предположений и дальнейшего их изучения.
Я рассмотрел ряд базовых методов для анализа ациклических направленных графов с помощью библиотек dagitty и ggdag, вместе с тем тема Causal Inference невероятно обширна и интересна.

/img/star (2).png.webp)



/img/news (2).png.webp)
/img/event.png.webp)
