Время прочтения: 4 мин.
С популяризацией темы графов, графовой аналитики и их визуализации, возрастает необходимость измерять / сравнивать / выявлять зависимости и различные иерархии. На основе метрик могут быть выявлены, как мошеннические схемы и аномалии, так и изучены пути распространения информации или даже извлечены дополнительные признаки для машинного обучения.
Граф – математический объект, представляющий отношения между сущностями, которые будут являться вершинами, связанными ребрами. Например, породы котиков — вершины, а происхождение одной породы из другой — ребра. Помимо некоторой структуры у графов так же могут быть количественные показатели, называемые метриками.
Графовая метрика – это функция, которая возвращает действительное число, характеризующее граф согласно применяемым мерам.
Рассмотрим следующие метрики:
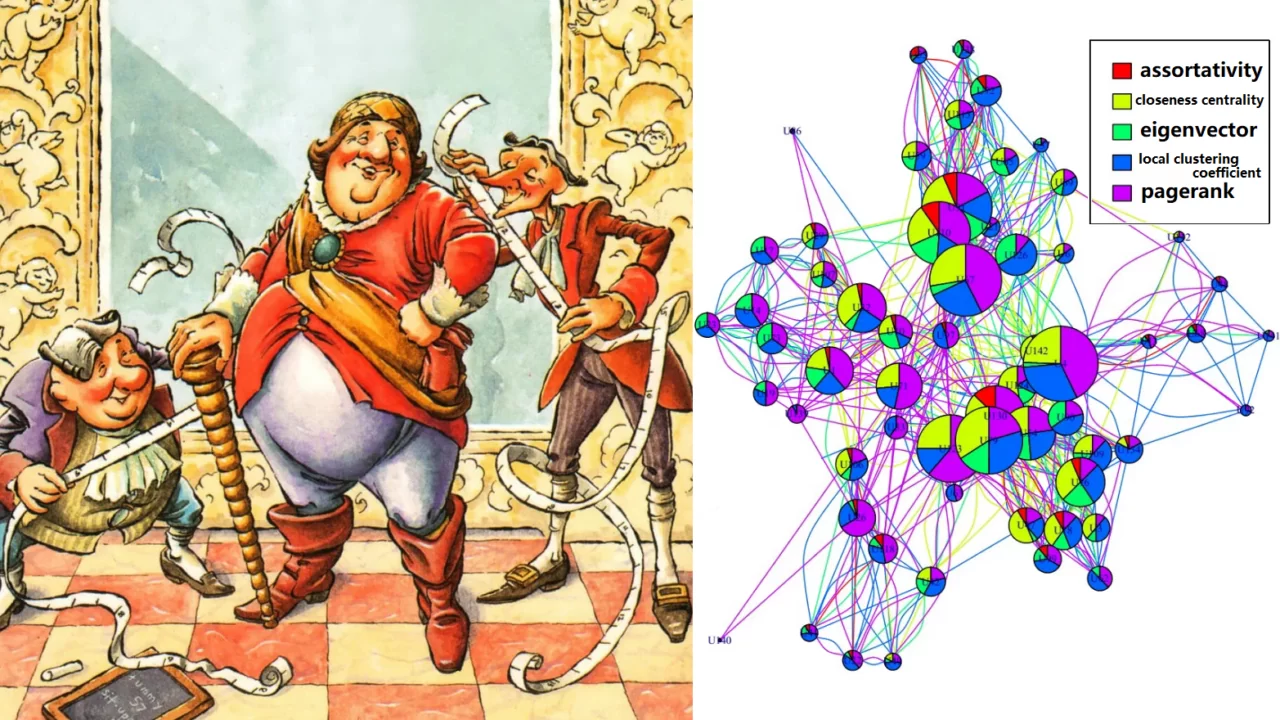
- Мера схожести вершин (Assortativity)
- Мера близости вершин (Closeness centrality)
- Мера влияния вершины в графе (Eigenvector)
- Мера связности соседних вершин (Local clustering coefficient)
- Мера важности вершины в графе (Pagerank)
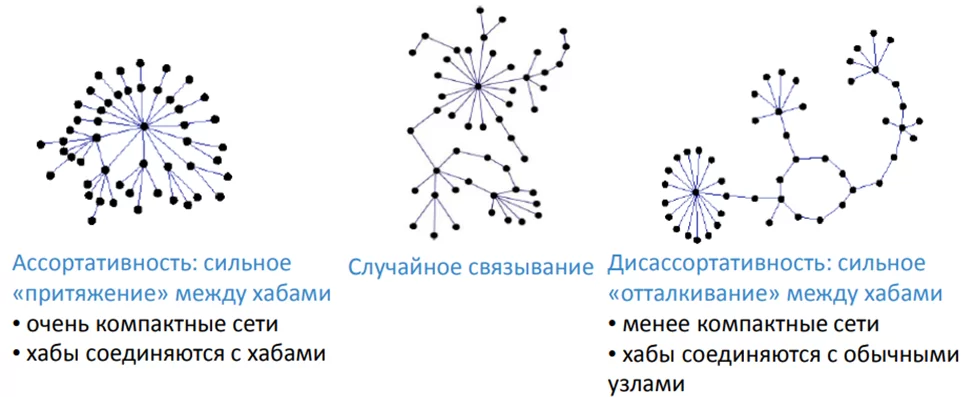
Одна из важных характеристик сложных сетей – коэффициент ассортативности – был впервые введен Ньюманом, как коэффициент корреляции Пирсона для степеней смежных вершин, теперь чаще встречается под названием «Мера схожести вершин».
Ассортативность – тенденция узлов графа соединяться с другими узлами того же типа. В узком смысле – тенденция связываться с узлами с тем же (близким) числом связей. Для упрощения понимания, главный вопрос этой меры: «Какие вершины схожи по количеству связей?»
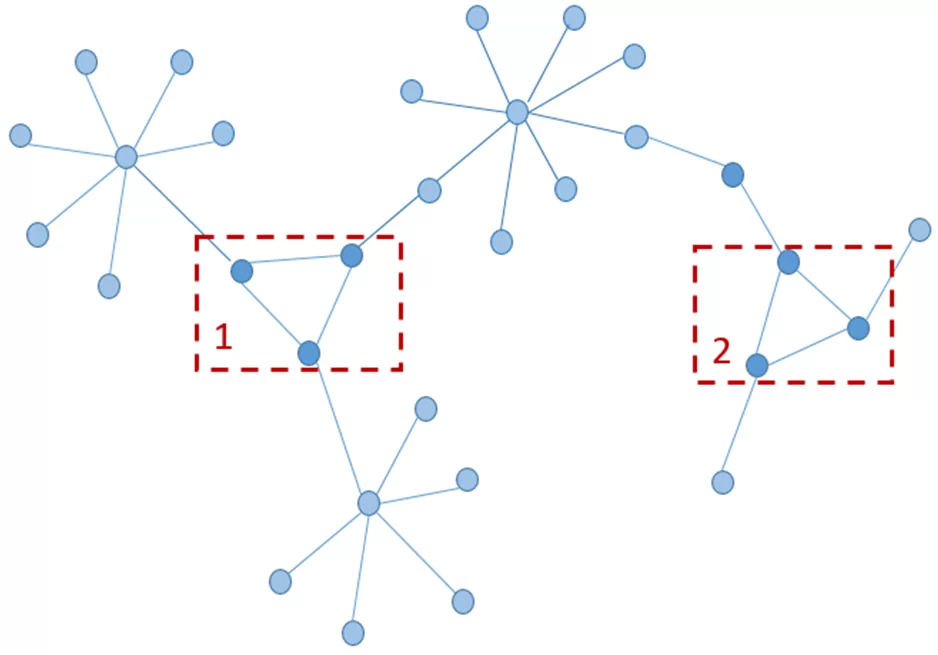
Использование такой меры может быть полезно, например, при поиске участников некоторых схем мошенничества с массовыми банковскими операциями.
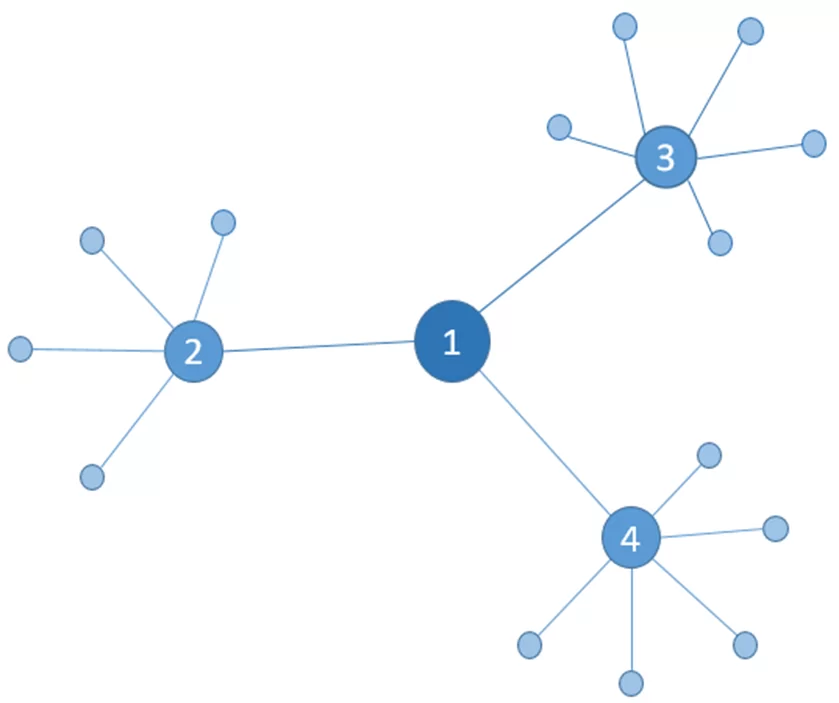
Следующая мера – мера близости вершин. Если описывать просто, то, чем ближе узел к центру графа, тем ближе он ко всем остальным узлам. Эта величина может быть вычислена, как единица, делённая на сумму длин кратчайших путей между узлом и всеми другими узлами графа. Основной вопрос меры: «Какая вершина находится ближе всех к остальным вершинам?».
Например, вершина 1 нуждается в наименьшем количестве переходов к другим вершинам.
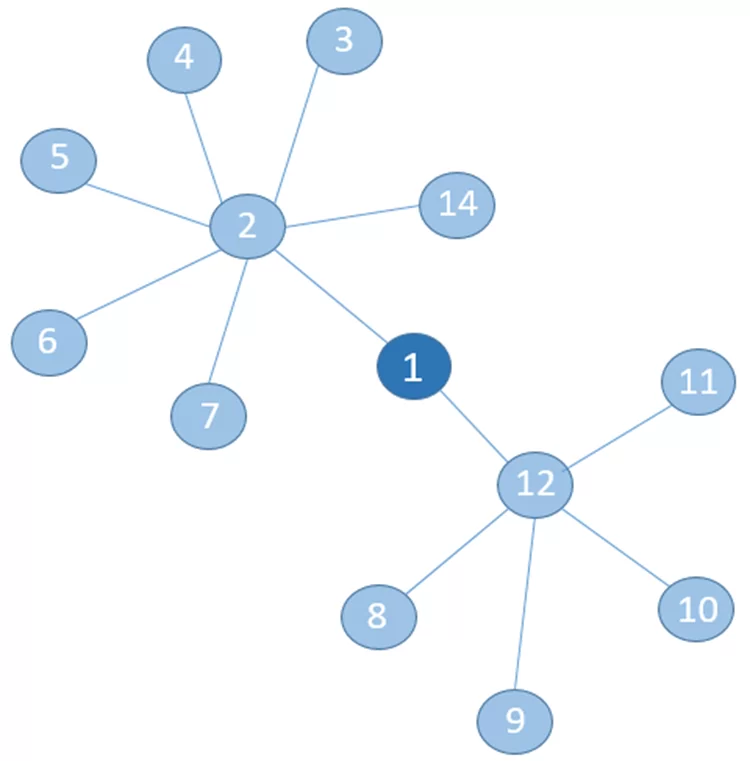
Мера влияния вершины – это мера, которая ранжирует или количественно выражает влияние каждого узла в графе. Вопрос меры: «Какая вершина является наиболее влиятельной в процессе?».
Например, вершина 1 может иметь меньше связей, но среди них все влиятельные, следовательно, она наиболее влиятельна.
Две вершины графа называют связанными, если между ними существует ребро. Любая вершина по определению связана сама с собой. Граф же считается связанным, если любая пара вершин в нем связана.
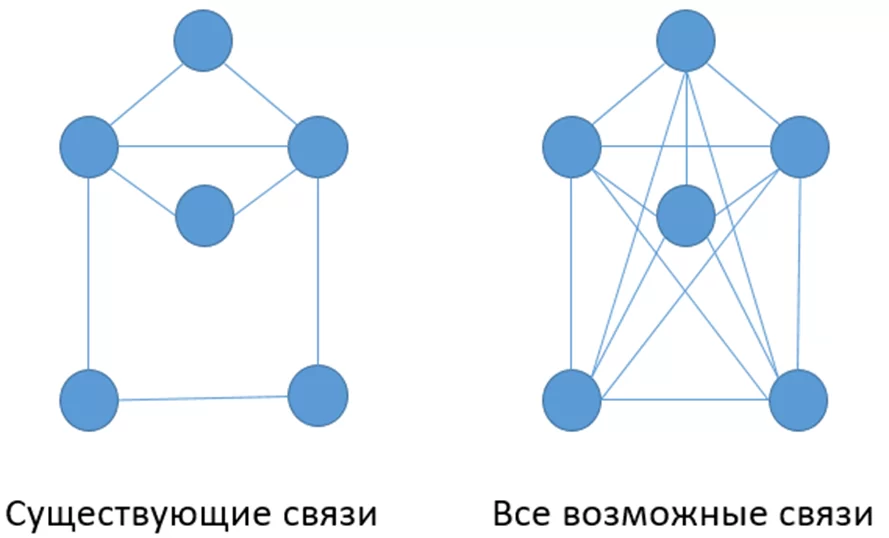
Мера же связности соседних вершин отвечает на вопрос: «Насколько плотно связана группа вершин?» и, соответственно, сравнивает количество существующих связей с количеством всех возможных связей.
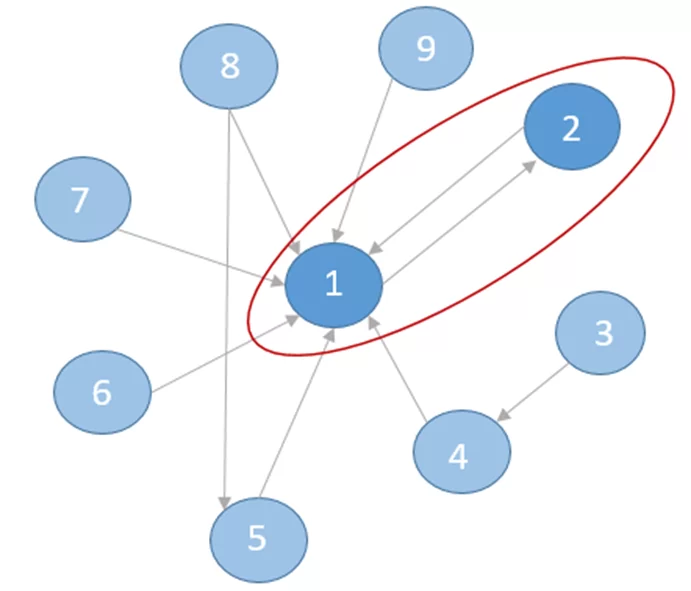
Мера важности вершины – это числовая величина, характеризующая «важность» каждой вершины. Чем больше входящих рёбер, тем она «важнее». Кроме того, «вес» вершины А определяется «весом» вершины-источника каждого входящего узла.
«Какая вершина имеет наибольшую важность?» – вопрос меры важности вершины.
Например, вершина 1 – самая влиятельная, имеет наибольшее число входящих связей; вершина 2 – вторая по влиянию, т.к. может влиять на вершину 1.
Графовый анализ эффективен, когда мы рассматриваем объекты в контексте связей с другими объектами. На этой основе можно сделать вывод о том, что использование графов не ограничивается узким набором областей.
В настоящее время в банковской сфере все больше графы применяются с практической точки зрения.
Так, автор использовал меры схожести и близости вершин для поиска операций в рамках мониторинга системы противодействия легализации (отмыванию) доходов.
Единственная проблема такого подхода – необходимость большого объёма данных; и в этом же его сильная сторона, так как мошенники не смогут смоделировать работу алгоритмов, а, значит, и остаться в тени у них не получится.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)