Время прочтения: 6 мин.
Прежде чем приступить к раскрытию темы, необходимо ознакомиться с общими понятиями.
Обратное распространение — это способ обучения нейронной сети. Цели обратного распространения просты: отрегулировать каждый вес пропорционально тому, насколько он способствует общей ошибке. Если мы будем итеративно уменьшать ошибку каждого веса, в конце концов у нас будет ряд весов, которые дают хорошие прогнозы.
Каждый узел в нейронной сети представляет собой нейрон, поэтому мы можем сказать, что нейронная сеть — это цепь нейронов.
Размышление, которые привели меня к использованию алгоритма обратного распределения:
- Прежде всего, если я хочу создать нейронную сеть мне нужно инициализировать некоторые веса.
- Какие бы значения я ни выбрала для весов, я не знаю насколько они верны.
- Чтобы проверить правильность или неправильность выбранных значений веса, я должна вычислить ошибку модели.
- Предположим, моя ошибка модели произошла слишком много раз.
- Это означает, что мой прогнозируемый результат сильно отличается от фактического. Так что мне делать? Постараюсь минимизировать ошибку.
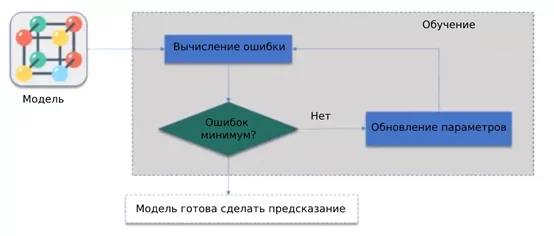
Описание схемы:
- Здесь мы пытаемся минимизировать нашу ошибку, как мы это сделаем?
- Что мы действительно хотим сделать, так это научить нашу модель изменять веса автоматически, чтобы получить наименьшее количество ошибок.
- Как показано на приведенной выше диаграмме, мы сначала вычислили ошибку нашей модели, после этого мы увидели, что если ошибка минимальна, то наша модель готова для прогнозирования.
- Если ошибка не минимизирована, мы обновим параметры (веса) и снова вычислим ошибку.
- Эти процессы будут выполняться до тех пор, пока ошибка нашей модели не будет сведена к минимуму.
Как работает алгоритм обратного распространения?
Предположим, у нас есть нейронная сеть с входным, скрытым и выходным слоями.
- Шаг 1: Сначала мы присваиваем модели случайные веса.
- Шаг 2: Прямое распространение (расчет обычной нейронной сети).
- Шаг 3: Вычислить общую ошибку.
- Шаг 4: Обратное распространение (градиентный спуск), обновление параметров (веса и смещение).
- Шаг 5: Пока ошибка не будет минимизирована (прогнозируемый результат будет примерно равен исходному результату).
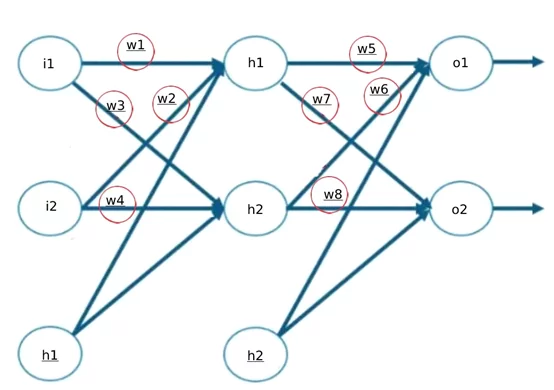
ПЕРЕДАЧА РАСПРОСТРАНЕНИЯ
- Рассчитать значение h1
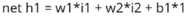
2. Рассчитать выход h1
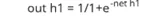
3. Рассчитать погрешность вывода h1
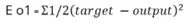
4. Вычислить общую погрешность модели

Теперь будет распространяться в обратном направлении
ОБРАТНОЕ РАСПРОСТРАНЕНИЕ
Здесь мы пишем процесс и формулы для обновления нашего веса w5.
Для этого мы должны знать, какая общая ошибка произошла по отношению к весу w5.
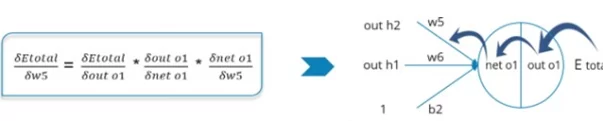
- Вычисление нашей общей полной ошибки относительно выходного

2. Расчет нашего общего output1по отношению к чистому output1

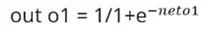
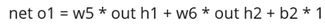
3. Расчет чистого output1 относительно weight5
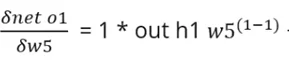
4. Расчет обновленного веса
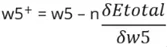
Аналогичным образом мы можем рассчитать и другие значения веса (весь этот процесс происходит в модели).
Как реализовано обратное распространение на Python?
Инициализация значения переменных:
import numpy as np
input_data = np.array(([2, 9], [1, 5], [3, 6]), dtype=float)
print("small x",input_data)
original_output = np.array(([92], [86], [89]), dtype=float)
max_in_axis = input_data /np.amax(input_data ,axis=0) #максимум по первой оси
print("Capital X",max_in_axis )
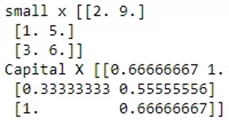
#Определение сигмоидной функции для вывода
def sigmoid input_data ):
return (1/(1 + np.exp(-input_data )))
#Производный от сигмовидной функции
def sigmoid_derivatives(input_data ):
return input_data * (1 - input_data )
#Инициализация переменных
epoch=7000 #Настройка итераций обучения
lr=0.1 #Установка скорости обучения
inputlayer_neurons_layer = 2 #количество нейронов входного слоя
hiddenlayer_neurons_layer = 3 #количество нейронов скрытых слоев
output_neurons_layer = 1 #количество нейронов на выходном слое
Пояснение:
В этом коде мы определили сигмовидную функцию и ее производную функцию.
Как вы знаете, мы обучаем нейронную сеть много раз в одной точке, для этого нам нужно количество эпох. Ниже мы определили единственное количество нейронов в каждом слое:
# Определение веса и смещения для скрытого и выходного слоя
bout=np.random.uniform(size=(1,output_neurons_layer))
weight=np.random.uniform(size=(inputlayer_neurons_layer ,hiddenlayer_neurons_layer ))
wout=np.random.uniform(size=(hiddenlayer_neurons_layer ,output_neurons_layer ))
bias=np.random.uniform(size=(1,hiddenlayer_neurons_layer ))
Пояснение:
Здесь мы определили случайные веса и смещение
Мы должны сначала определить wights и Bias для первого (здесь у нас только один скрытый слой) скрытого слоя.
После этого мы определили веса и смещение для выходного слоя.
Определяя размер весов, стоит помнить: сколько нейронов в предыдущем слое, количество нейронов в слое, для которого мы определили веса.
Размер смещения (количество нейронов в выходном слое, количество нейронов в слое, для которого мы определили смещения)
#Прямое распространение
for i in range(epoch):
hinp1=np.dot(max_in_axis ,weight)
hinp=hinp1 + bias
hlayer_act = sigmoid(hinp)
outinp1=np.dot(hlayer_act,wout)
outinp= outinp1+ bout
output = sigmoid(outinp)
Пояснение:
Здесь мы просто вычисляем выходные данные нашей модели, сначала мы сделали это для скрытого слоя, а затем для выходного слоя и, наконец, получили результат.
np.dot используется для скалярного произведения двух матриц
#Backpropagation алгоритм
EO = y-output
outgrad = sigmoid_derivatives(output)
d_output = EO* outgrad
EH = d_output.dot(wout.T)
hiddengrad = sigmoid_derivatives(hlayer_act)
#сколько скрытых слоев привело к ошибке
d_hiddenlayer = EH * hiddengrad
wout += hlayer_act.T.dot(d_output) *lr
bout += np.sum(d_output, axis=0,keepdims=True) *lr
#Обновление веса
weight += max_in_axis.T.dot(d_hiddenlayer) *lr
print("Actual Output: \n" + str(y))
print("Predicted Output: \n" ,output)
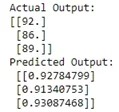
В этом коде сначала мы вычислили ошибку выходного слоя.
Как мы знаем из формулы, мы должны выяснить, какой вклад скрытого слоя в общую ошибку, а также вклад веса в общую ошибку.
После этого мы обновили наши веса и смещения, пока не получим минимальную ошибку.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
