Время прочтения: 4 мин.
Основная наша работа связана с анализом и воспроизводством разнообразных моделей. В один прекрасный день, когда мы тихо кодили и никого не трогали нам поступила задача, связанная с классификацией отчетов по проверке моделей.
Отчет по проверке моделей – это итоговый документ, где описывается модель, для чего она предназначена, какие исходные данные она использует и самое главное – то, на основании чего отчет и классифицируется – итоговые показатели и метрики модели. Выглядит это примерно вот так:
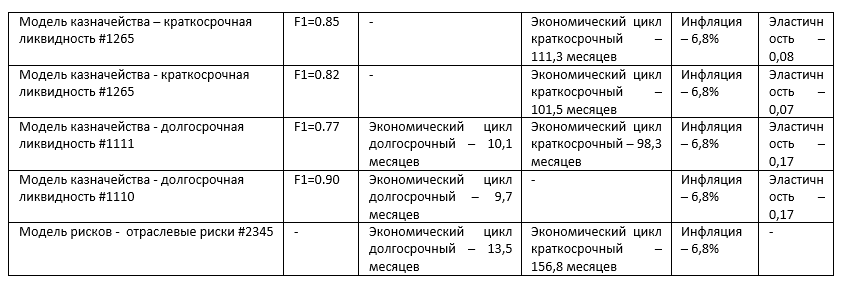
При этом количество видов классификаций было неизвестно, а количество признаков для классификации было разным (от 1 до 50 показателей), признаки могли присутствовать или отсутствовать в разных видах отчетов. Для решения данной задачи было решено использовать нейросети.
Раньше мы абсолютно не имели практического опыта построения нейронных сетей. При этом по причине необходимости постоянно использовать Python в работе мы достаточно неплохо знали стандартные библиотеки Python, в том числе библиотеку Numpy, а также неплохо представляли себе теорию построения нейросеток.
Мы начали разбираться, как нам на основе имеющегося опыта с минимальными трудозатратыми, и не тратя дополнительно время на изучение новых библиотек, выполнить эту задачу. В результате, мы получили вполне работающую схему построения нейросети на основе Numpy, реализовали простейшую нейросеть с одним скрытым слоем принимающую на вход 3 параметра на python с использованием библиотеки Numpy, о которой и пойдет речь далее.
Начнем, как говорится, с начала. Нейросеть реализуем через класс, с методами, реализующими весь функционал. Для начала инициализируем через конструктор входные параметры — learning_rate=0.05, начальные веса – захардкодим (протекционисты могут заюзать функцию random).
class simpleNeiroNet(object):
def __init__(self, learningRate=0.05):
# инициируем базовые веса не нулевыми значениями
self.w_0_1 = np.random.normal(0.5, - 0.5, (0.5, 0.5)) # веса первого слоя
self.w_1_2 = np.random.normal(0.25, 0.25, (0.25, 0.25)) # веса второго слоя
self.functionMapper = np.vectorize(self. thFunction)
self.learningRate = np.array([learningRate])
В качестве функции активации мы решили использовать гиперболический тангенс, но его легко заменить любой другой функцией, к примеру, сигмоидом.
def thFunction(self, x):
return (2 / (1 + np.exp(2 * -x)) – 1)
В качестве функции потерь, которая показывает насколько отклоняются предсказания и реальные показатели, мы используем MSE.
def lossMSE(yPredict, yReal):
return np.mean((yPredict - yReal)**2)
Далее получаем предсказанные значения.
def predictValues(self, inputData):
# считаем первый слой
inputDataFirst = np.dot(self.w_0_1, inputData)
outputDataFirst = self.sigmoid_mapper(inputDataFirst)
# считаем второй слой
inputDataSecond = np.dot(self.w_1_2, outputDataFirst)
outputDataFirstSecond = self.functionMapper(inputDataSecond)
return outputDataFirstSecond
Тренируем веса:
def train(self, inputData, expectedPredict):
# считаем первый слой
inputDataFirst = np.dot(self.w_0_1, inputData)
outputDataFirst = self.functionMapper(inputDataFirst)
# считаем второй слой
inputDataSecond = np.dot(self.w_1_2, outputDataFirst)
outputDataSecond = self. functionMapper(inputDataSecond)
actualPredict = outputDataFirstSecond[0]
errorLayerSecond = np.array([actualPredict - expectedPredict])
gradientLayerSecond = actualPredict * (1 - actualPredict)
weightsDeltaLayerSecond = errorLayerSecond * gradientLayerSecond
self.w_1_2 -= (np.dot(weightsDeltaLayerSecond, outputDataFirstSecond.reshape(1, len(outputDataFirstSecond)))) * self.learningRate
errorLayerFirst = weightsDeltaLayerSecond * self.w_1_2
gradientLayerFirst = outputDataFirst * (1 - outputDataFirst)
weightsDeltaLayerFirst = errorLayerFirst * gradientLayerFirst
self.w_0_1 -= np.dot(inputData.reshape(len(inputData), 1), weightsDeltaLayerFirst).T * self.learningRate
Следующим шагом задаем количество эпох, другими словами, сколько раз будем считать и проводим тренировку весов, расчет предсказаний и их сравнение с фактом, в общем используем все функции, описанные ранее:
numberOfEpochs = 6000
learningRate = 0.08
neuralNetwork = simpleNeiroNet(learningRate = learningRate)
for epoch in range(numbersOfEpochs):
inputTemp = []
correctPredictions = []
for inputStat, correctPredict in train:
neuralNetwork.train(np.array(inputStat), correctPredict)
inputTemp.append(np.array(inputStat))
correctPredictions.append(np.array(correctPredict))
trainLoss = lossMSE(neuralNetwork.predict(np.array(inputTemp).T), np.array(correctPredictions))
sys.stdout.write(
"\r percent of progress: {}, Training loss: {}".format(
str(100 * epoch / float(numberOfEpochs))[:4], str(trainLoss)[:5]))
И на выходе получаем:
Percent of progress: 99.9, Training loss: 0.001В результате работы нейросети был получен отчет с классифицированными моделями.
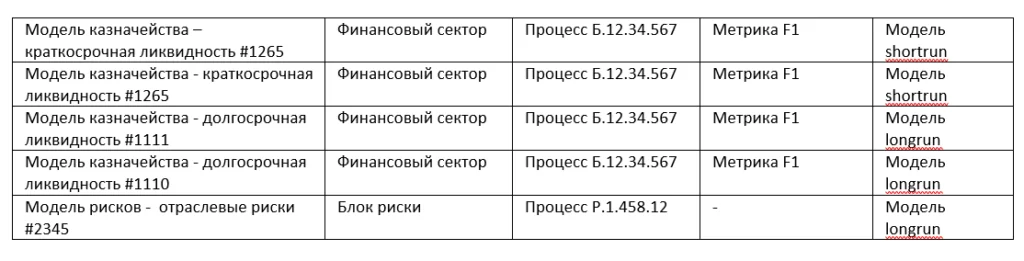
Конечно, окончательная классификация потребовала «посмотреть глазами» полученные результаты – но это было уже проверка агрегированных данных – что гораздо проще – чем вручную провести просмотр и классификацию многих сотен документов, плюс нами был разработан инструмент, который можно использовать при последующих классификациях.
Итого, мы написали самую простую нейросеть и опробовали на ней осуществить несложные предсказания.
Всегда полезно не только понимать теоретически как работает «под капотом» тот или иной метод, но и уметь реализовать такой метод в коде, причем максимально используя уже имеющийся опыт. Именно подобный навык отличает программиста от того, кто программистом только называется.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
