Время прочтения: 8 мин.
Доброе утро! Эта публикация — вторая часть небольшого цикла, посвящённого алгоритмам вложений вершин графа в векторное пространство. Сегодня рассмотрим главную идею алгоритмов, основанных на случайных блужданиях. Перед прочтением рекомендую прочитать первую часть.
Вспоминаем о школьнике-разработчике
В предыдущей части старшеклассник из школы X всё-таки смог создать систему рекомендаций друзей для своей школьной социальной сети и вывести свой продукт на новый уровень. Казалось бы, всё отлично, пользователей всё больше, алгоритмы хорошо работают, сеть развивается. Но вот проблема — конкуренты не дремлют. Ученик школы Y (дальше будем называть его старшеклассник Y), у которого тоже (вот совпадение) есть своя социальная сеть, решил отобрать славу своего конкурента. Но поскольку одна социалка уже есть, для успешного соперничества ему необходимо создать систему ещё лучше или хотя бы на том же уровне.
На первом этапе было принято решение начать работу над новым алгоритмом. Старшеклассник Y знал, что его конкурент каким-то образом умеет превращать граф в простые числовые векторы. Теперь главная цель конкурента — узнать, как это можно сделать, и применить знание на благо собственного ресурса.
Начало работы
У старшеклассника Y были старые книги по теории вероятностей и теории случайных процессов, которые он любил листать перед сном, чтобы скорее заснуть, смотря на странные рисунки и малопонятные определения и формулировки.
Но всё же некоторые определения иногда запоминались, причём весьма неплохо. Вот некоторые из них:
Случайная величина — численное представление результата какого-либо случайного события. Например, количество очков при бросании кубика.
Случайный процесс — индексированное множество случайных величин. В основном индексами являются точки во времени или координаты.
Марковское свойство случайного процесса. Свойство говорит о том, что информация о поведении процесса в прошлом не даст никакой информации о том, как он будет вести себя в будущем, поскольку будущее состояние процесса зависит только от текущего состояния. Процесс с таким свойством называется Марковским процессом.
Цепь Маркова — это Марковский процесс, у которого не более чем счётное число состояний. То есть число состояний либо конечное, либо равномощно множеству натуральных чисел.
Подведение к решению
Давайте пока отвлечёмся от социальных сетей и противостояний школьников и их социальных сетей. Вместо этого предлагаю подумать над следующей задачей. Существует необходимость создать клавиатуру с автонабором. Автонабор должен по написанному слову определить следующее, которое наиболее вероятно идёт за ранее написанным. *доброе* 🡪 *утро*, *как* 🡪 *дела* и тому подобное. Мы можем рассматривать предложение как некий случайный процесс, состоянием на шаге i является i-ое слово в предложении.
Вот наш корпус:
Белый снег, белый мел, белый заяц тоже бел. А вот белка не бела — белой даже не была.
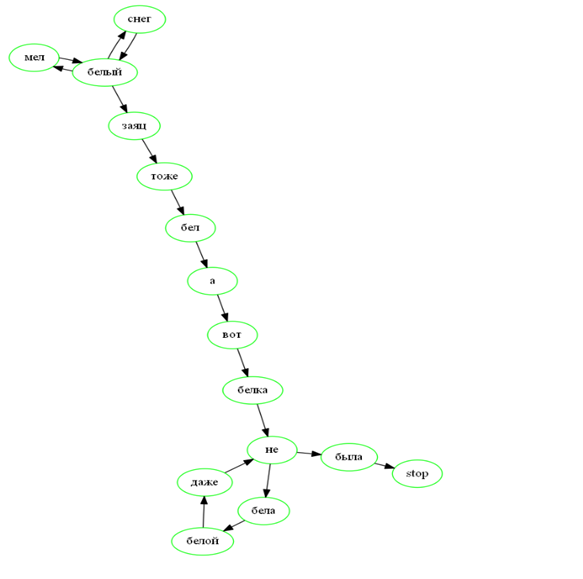
Используя эту информацию, строим Марковскую цепь.
Пусть пользователь написал слово *вот*. Тогда из возможных вариантов продолжения (основываясь на нашем корпусе) будет слово *белка*. А слово *белый* более интересно, после него могут идти слова: *снег*, *заяц*, *мел*. Марковские цепи с конечным числом исходов удобно изображать с помощью взвешенных, ориентированных графов, где весы — это вероятности перехода из одной вершины в другую вершину.
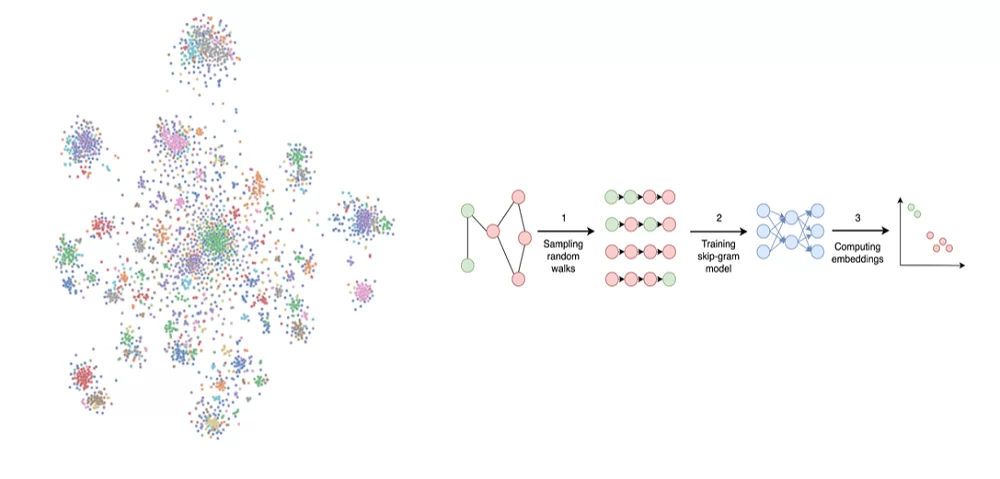
Если вы знакомы с алгоритмом Word2Vec, вы, вероятно, догадываетесь, что сейчас произойдёт. Если говорить кратко, то Word2Vec — это алгоритм, который предназначен для получения векторных представлений слов. Он базируется на дистрибутивной гипотезе, согласно которой смысл слова определяется по его соседям, то есть по контексту. А что если принять эту гипотезу и для вершин графа?
Например, при анализе социальных сетей, строя граф отношений между людьми, можно также предположить характер человека, его интересы и так далее, ссылаясь на интересы и характер его друзей. Давайте решим обратную задачу. Есть граф, и нужно генерировать предложения (точнее, последовательности вершин) для того, чтобы передавать его алгоритму Word2Vec.

Последний объект, который понадобится, — так называемая матрица перехода. В нашем простом случае матрица перехода очень напоминает матрицу смежности, только теперь в элементе a (i, j)будет находиться вероятность перехода и i-ой вершины в j-ую. Отсюда простое свойство. Сумма элементов строки матрицы = 1.
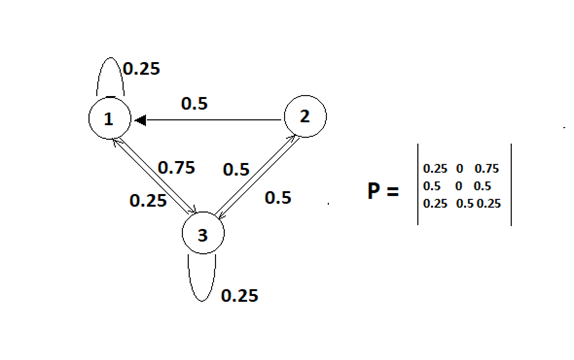
Предположим, что сейчас я нахожусь в точке 1. Если я умножу вектор v= [1, 0, 0] (что можно интерпретировать как вероятность нахождения в точке 1 = 1, в точке 2 = 0, в точке 3 = 0) на матрицу P, то получу вероятности попадания в вершины на следующем шаге (в данном случае вероятность попасть в 1 = 0.25, 2 = 0, 3 = 0.75).
import numpy as np
start = np.array([1, 0, 0])
step = ([[0.25, 0, 0.75],
[0.5, 0, 0.5],
[0.25, 0.5, 0.25]])
next_p = start @ stepТакже я могу посчитать вероятность нахождения в вершинах на n-ом шаге.
Пусть, например, n = 20, и я на первом шаге равновероятно попадаю или в 1, или 2, или 3 вершину.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
start = np.array([0.33, 0.33, 0.34])
step = np.array([[0.25, 0, 0.75],
[0.5, 0, 0.5],
[0.25, 0.5, 0.25]])
history = []
for n in range(20):
start = start @ step
history.append(start)
plt.imshow(history)
print(start)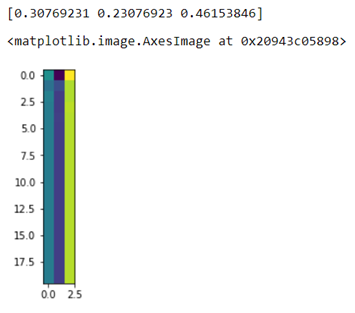
Матрицы перехода — очень удобный инструмент для работы с такими математическими объектами.
Ну а теперь возвращаемся к социальным сетям, школьникам и алгоритмам. Итак, сейчас ключевая задача старшеклассника Y — написать простой генератор последовательностей вершин, вот его план:
- На вход генератору подаётся матрица перехода интересующего графа.
- Из каждой вершины совершается блуждание n раз.
- Переход из вершины i (текущее состояние процесса) в вершину i+1 (следующее состояние процесса) осуществляется с помощью матрицы перехода и функции random.choice из библиотеки numpy (матрица перехода выдаёт вероятностное распределение случайных величин, а функция random.choice случайным образом выбирает одну из них, учитывая вероятности, после чего текущее состояние меняется на выбранное значение, а предыдущее состояние запоминается).
- Шаг 3 повторяется m раз.
- Полученная последовательность складывается в общий корпус последовательностей, затем этот корпус будет передан в Word2Vec.

К делу
Наконец-то! Теперь у старшеклассника школы Y есть всё необходимое для того, чтобы реализовать простой генератор случайных блужданий на графе.
У генератора есть 2 параметра: количество шагов блуждания (глубина блуждания) и количество блужданий из i-ой вершины. Полученные последовательности нужно отдавать алгоритму Word2Vec.
Для тестирования вернусь к графу из предыдущей статьи. Матрицу перехода получим из матрицы смежности, для этого каждый элемент матрицы смежности необходимо поделить на сумму элементов той строки, где этот элемент находится.
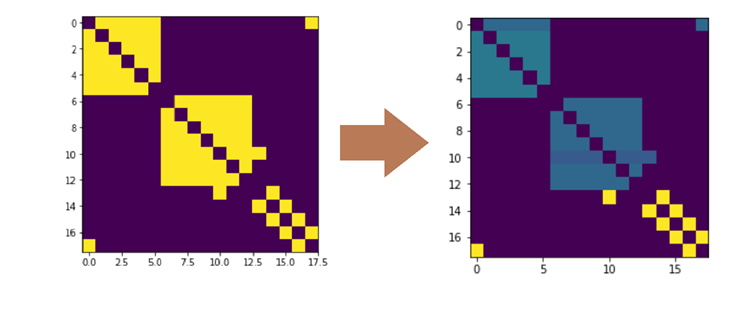
import numpy as np
class RandomWalks:
def __init__(self, markov_chain, node_names, count_steps, count_walks):
self.__M = markov_chain
self.__count_nodes = self.__M.shape[0]
self.__count_steps = count_steps
self.__count_walks = count_walks
self.__node_names = node_names
self.__start_points = np.eye(self.__count_nodes)
def walk(self, start, start_index):
walk = [self.__node_names[start_index]]
for _ in range(self.__count_steps):
prop = start @ self.__M
node_index = np.random.choice(np.arange(0, self.__count_nodes), p=prop)
walk.append(self.__node_names[node_index])
start = self.__start_points[node_index]
return walk
def get_random_walks(self):
random_walks = []
for index, item in enumerate(self.__start_points):
for _ in range(self.__count_walks):
random_walks.append(self.walk(item, index))
return random_walks
from gensim.models import Word2Vec
#имена вершин
name_node = [str(i) for i in range(18)]
#экз. класса случайных блужданий
rw = RandomWalks(mc, name_node, 7, 30) #mc — матрица перехода
#корпус последовательностей вершин
corpus = rw.get_random_walks()
#модель word2vec
model = Word2Vec(corpus, vector_size=2, window=5, epochs=100)
#полученные векторы
vectors = [model.wv[item] for item in name_node]
Давайте сравним данные векторы с векторами, полученными матричной факторизацией. Если вы не очень понимаете, о чём идет речь, то рекомендую прочитать первую часть цикла.
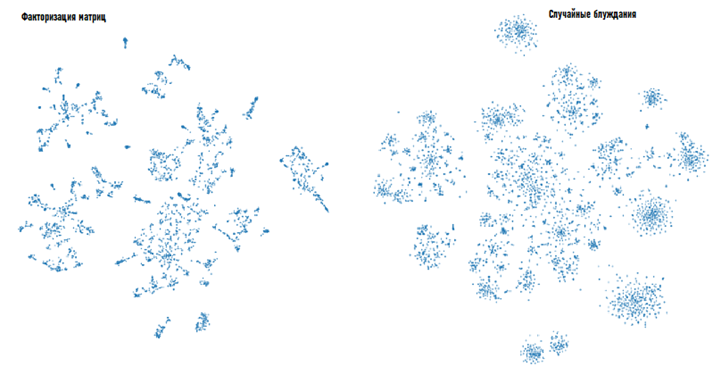
Теперь остаётся лишь применить какой-нибудь алгоритм кластеризации, например, DBSCAN.
from sklearn.cluster import DBSCAN
import seaborn as sns
df_scatterplot = pd.DataFrame(emb, columns=['e1', 'e2'])
df_scatterplot['label'] = DBSCAN(eps=1, min_samples=2).fit(emb).labels_
plt.figure(figsize=(10, 10))
sns.scatterplot(data=df_scatterplot, x='e1', y='e2', hue='label', s=8, palette='deep')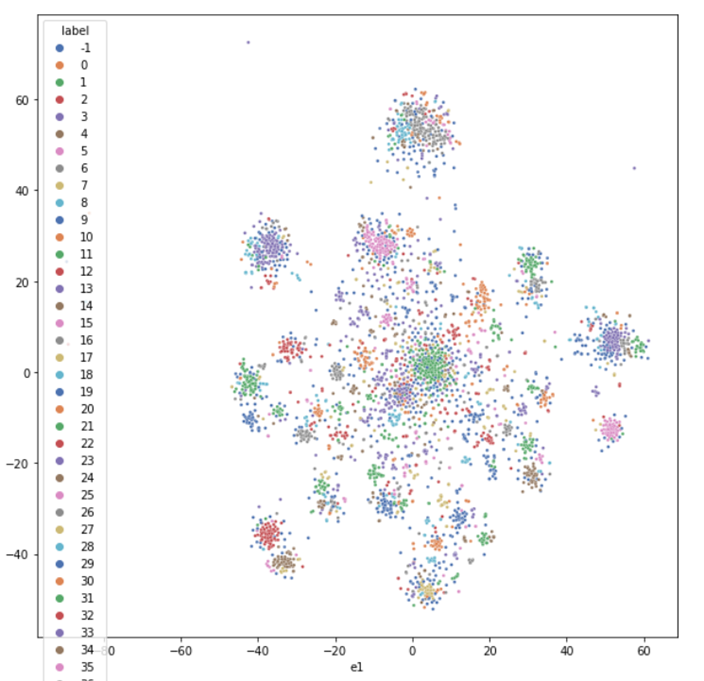
Схема остаётся такой же, пользователю будем рекомендовать человека, который находится с ним в одном кластере и при этом не дружит. Алгоритм может служить как механизм отсеивания, сначала можно убрать маловероятные варианты дружбы, иначе проверка каждого пользователя займёт весьма много времени и ресурсов.
На этом, собственно, всё. Сегодня я рассмотрел алгоритм вложения графа, который основан на случайных блужданиях, и помог старшекласснику Y создать свою простую рекомендательную систему друзей, причём ничуть не хуже, чем у старшеклассника X. Есть алгоритмы и получше. Например, алгоритм Node2Vec использует Марковское свойство второго порядка. Зная нюансы этих свойств, вы без особого труда в нём разберётесь.
К слову, задача вложения графов стала самостоятельной задачей машинного обучения, и теперь существуют целые нейросетевые архитектуры, посвящённые только её решению. Однако это не значит, что предложенные инструменты малоэффективны и нужно использовать только нейросети. Они всё ещё являются отличным инструментом при решении задач анализа графов, которые могут возникать в вашей работе.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)