Время прочтения: 5 мин.
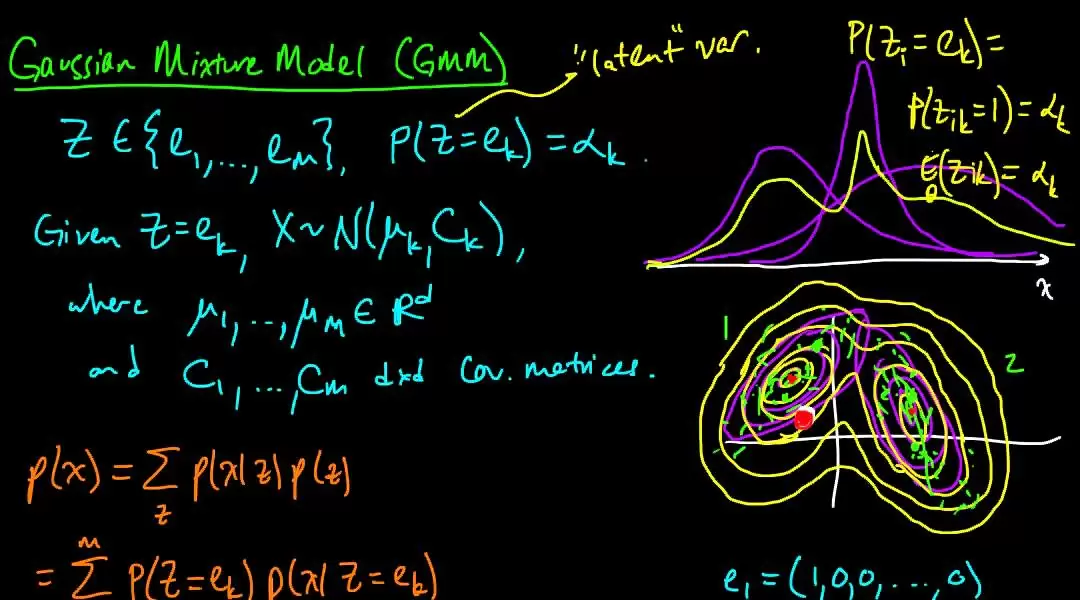
В данной статье я решил исследовать применение процессов Дирихле – Dirichlet process Gaussian mixture models (DPGMM) в машинном обучении, которые могут быть полезны при небольшом объеме данных. Я не буду углубляться в математическую часть, однако дам краткое описание и рассмотрю применение алгоритма к задаче классификации.
Упрощенно говоря, Gaussian mixture models (GMM) можно представить, как алгоритм кластеризации, в котором каждое наблюдение может принадлежать к более чем одному кластеру. Это способ представить данные как образцы из смеси распределений. На выходе DPGMM – смесь распределений с известными параметрами (средние и матрицы ковариаций) и разными пропорциями. Для подбора параметров GMM применяет алгоритм максимизации ожидания (Expectation-maximization), используя в процессе теорему Байеса. Выход модели — это не вероятность принадлежности к какому-либо классу, а правдоподобие, поэтому его нельзя использовать напрямую для определения класса.
В своем примере я использовал данные семян, состоящие из признаков для трёх различных сортов пшеницы по 70 элементов в каждом.
Верхний срез данных:
df.head()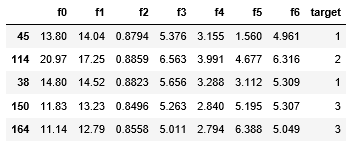
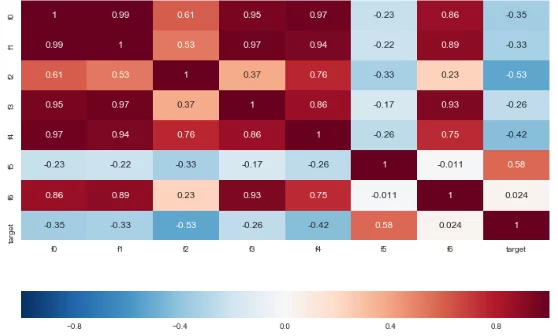
Некоторые столбцы сильно коррелированы, данные не нормированы,
c_matrix_test = df.corr()
plt.figure(figsize=(12, 8))
sns.heatmap(c_matrix_test, vmin=-1, annot=True, fmt='.2g', cbar_kws={"orientation": "horizontal"})
plt.show()
Переходим непосредственно к процессу обучения. Я взял имплементацию из библиотеки sklearn. Используя точки, принадлежащие одному классу, обучил на них DPGMM и оценил для каждой точки log-likelihood по обученной модели. Затем повторил это для всех классов и получил три новых признака, по одному на каждый класс. Так же разбил данные на train и test.
df1 = df[df.target == 1]
df2 = df[df.target == 2]
df3 = df[df.target == 3]
log_likelihood = []
for X in [df1, df2, df3]:
dpgmm = BayesianGaussianMixture(
n_components=3, covariance_type='full',
weight_concentration_prior_type='dirichlet_process',
init_params='kmeans', random_state=422).fit(X)
log_likelihood.append(dpgmm.score_samples(df))
dpgmm_1 = log_likelihood[0]
dpgmm_2 = log_likelihood[1]
dpgmm_3 = log_likelihood[2]
dpgmm_f = pd.DataFrame({'dpgmm1': dpgmm_1, 'dpgmm2': dpgmm_2, 'dpgmm3': dpgmm_3})
df_dpgmm = pd.concat([df, dpgmm_f], axis=1)
df_dpgmm1 = df_dpgmm[df_dpgmm.target == 1]
df_dpgmm2 = df_dpgmm[df_dpgmm.target == 2]
df_dpgmm3 = df_dpgmm[df_dpgmm.target == 3]
test = pd.concat([df_dpgmm1.sample(24), df_dpgmm2.sample(24), df_dpgmm3.sample(24)], axis=0)
test_t = test.target
test.drop('target', axis=1, inplace=True)
test.head(10)
dpgmm_train = df_dpgmm.drop(test.index.values, axis=0)
dpgmm_X = dpgmm_train.drop('target', axis=1)
dpgmm_y = dpgmm_train.target
X_dpgmm_only = dpgmm_X[['dpgmm1', 'dpgmm2', 'dpgmm3']]
train = df.drop(test.index.values, axis=0)
X = train.drop('target', axis=1)
y = train.target
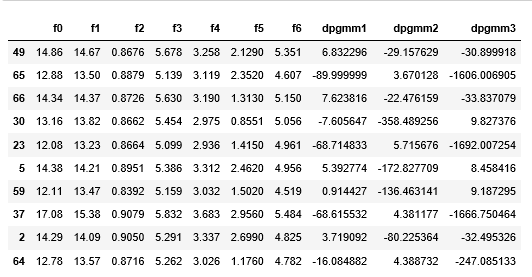
Вот так выглядят данные с признаками из DPGMM:
Теперь посмотрим и сравним как показывают себя некоторые модели на данных без признаков из DPGMM и на данных с ними. Выполним кросс-валидацию на тренировочных данных и сравним их с результатом на тестовых данных.
Результат кросс-валидации на тренировочных данных:
k_fold = KFold(n_splits=3, shuffle=True, random_state=1111)
names = ['Random Forest',
'Bagging Classifier',
'Gradient Boosting', 'Extra Trees']
classifiers = [
RandomForestClassifier(n_jobs=-1,max_depth=5, random_state=111),
BaggingClassifier(n_jobs=-1, random_state=111),
GradientBoostingClassifier(random_state=111, max_depth=5),
ExtraTreesClassifier(n_estimators=100, max_depth=5, n_jobs=-1, random_state=111)
]
for name, classifier in zip(names, classifiers):
start = time.time()
acc = []
for train_index, val_index in k_fold.split(X, y):
X_train, X_val = X.iloc[train_index], X.iloc[val_index]
y_train, y_val = y.iloc[train_index], y.iloc[val_index]
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_val)
acc.append(accuracy_score(y_val, y_pred))
print('The model used :', name)
print('ACC : {} '.format(sum(acc) / 3))
print('Duration : {} seconds'.format(round(time.time() - start, 2)))
print('_' * 60)
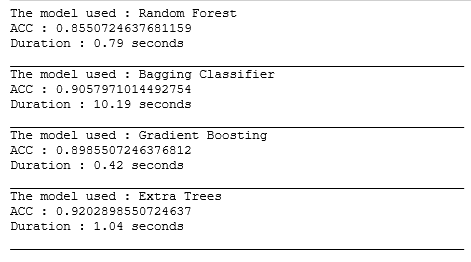
Результат на тестовых данных без признаков DPGMM:
for name, classifier in zip(names, classifiers):
start = time.time()
classifier.fit(X, y)
y_pred = classifier.predict(test.drop(['dpgmm1','dpgmm2','dpgmm3'], axis=1))
print('The model used :', name)
print('ACC : ', accuracy_score(test_t, y_pred))
print('Duration : {} seconds'.format(round(time.time() - start, 2)))
print('_' * 60)

И с признаками DPGMM:
for name, classifier in zip(names, classifiers):
start = time.time()
classifier.fit(dpgmm_X, dpgmm_y)
y_pred = classifier.predict(test)
print('The model used :', name)
print('ACC : ', accuracy_score(test_t, y_pred))
print('Duration : {} seconds'.format(round(time.time() - start, 2)))
print('_' * 60)

В данной статье я поэкспериментировал с признаками из DPGMM. Добавив к данным только лишь их, уже удалось получить улучшение по метрике accuracy в алгоритмах Random Forest Classification и Bagging Classifier на ≈ 5 процентов (0.85 и 0.9 против 0.9 и 0.95 соответственно), однако алгоритмы Gradient Boosting Classifier и Extra Trees Classifier напротив потеряли в точности, что оставляет нам простор для будущих исследований. Возможно, если бы мы подошли к каждому алгоритму отдельно и попробовали настроить под них свой тип ковариации, количество компонентов смеси и другие параметры, то результат был бы другой.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)