Время прочтения: 9 мин.
Недавно у меня возникла задача, в процессе которой потребовалось нечеткое сравнение строк. Ниже кратко опишу суть.
Проблема: на входе большое количество сканов документов в pdf формате, которые с помощью Adobe FineReader переведены в текстовые документы формата docx и мне необходимо произвести некоторую классификацию. К счастью тренировать NLP модель для этого не потребуется, т.к. документы легко классифицируются по содержанию в них конкретной фразы и мне остается лишь определить есть ли эта фраза в документе. С другой стороны, я еще далек от идеального будущего, в котором computer vision правильно распознает даже скан плохого качества, и поэтому текст в формат docx трансформировался с ошибками. Например, фраза «объект залога» может превратиться в «обb ект %алога».
Задача: написать функцию, которая определяет есть ли в документе определенная формулировка, с учетом неправильного преобразования текста.
С чего начнем?
Прежде чем бежать писать функцию, надо определиться каким методом производить нечеткое сопоставление строк. Выбор тут не самый широкий, было решено протестировать три варианта: сравнение по косинусному сходству; сравнение по сходству Левенштейна; сравнение по сходству Джаро-Винклера. Критерии, по которым предстоит выбрать лучший вариант: скорость выполнения (документов довольно много, нужно находить подстроку за разумное время); правильность сравнения (нечеткое сравнение на то и нечеткое, потому что требуется некая экспертная оценка того, как отрабатывает критерий сравнения), простота реализации.
Кратко о сути метрик
Сходство по Левенштейну. За основу берется расстояние Левенштейна – редакционное расстояние между словами, грубо говоря, сколько нужно сделать изменений символов в одном слове (строке), чтобы получить другое слово (строку). В стандартном варианте три вида изменений символа: вставка; удаление; замена. (в библиотеке rapidfuzz используется модифицированная версия этой метрики).
Сходство Джаро-Винклера. За основу берется расстояние Джаро (d), задается коэффициент масштабирования (p), не превышающий 0.25 и считается длина совпадающего префикса (комитет – комок; тут l = 3).
Получается следующая формула:
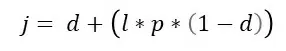
Расстояние Джаро считается следующим образом:
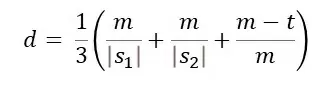
Где:
- m – сумма точных и неточных совпадений (неточное совпадение – если буквы в словах совпадают, но в разных позициях);
- t – количество неточных совпадений деленное на 2;
- |s1| и |s2| — длины первой и второй строки соответственно.
Косинусное сходство. Для вычисления необходимо сначала произвести векторизацию строки, в качестве токена для векторизации могут выступать буквы, слова, предложения. В данном случае будут использоваться буквы. Пример: два слова baba и abba, в сумме уникальных букв 2, соответственно имеется двумерное пространство. Пусть первая ось – это ось буквы a, вторая ось – это ось буквы b. Получаю два вектора baba – [2,2] и abba – [2,2], абсолютно идентичные векторы и косинусное сходство между словами равно 1 (нужно вычислить косинус между векторами). Если строка состоит только из кириллицы, максимальная размерность пространства будет равна 33 по количеству букв в алфавите.
Как буду тестировать?
На помощь придут python-библиотеки: rapidfuzz; sklearn.
С sklearn, я думаю, почти все знакомы, а rapidfuzz – это улучшенная версия thefuzz (fuzzywuzzy) написанная на C++, у которой есть API на многих языках, в том числе python, она априори быстрее чем thefuzz и обладает расширенным функционалом (присутствуют дополнительные метрики, например, сходство Джаро-Винклера, которое нам еще пригодится). Теперь перейду к вопросу тестирования.
Скорость: напишу функции для каждой метрики; прогоню их на тестовом документе; сравню время выполнения на многих языках, в том числе python, она априори быстрее чем thefuzz и обладает расширенным функционалом (присутствуют дополнительные метрики, например, сходство Джаро-Винклера, которое мне еще пригодится). Теперь перехожу к вопросу тестирования.
Правильность: сделаю несколько тестовых кейсов; измерю ключевые метрики, находящиеся в диапазоне от 0 до 1:
- Короткие строки, отличающиеся незначительно (орфографически).
- Короткие строки, значительно отличающиеся друг от друга (орфографически).
- Длинные строки, незначительно отличающиеся друг от друга (орфографически).
- Длинные строки, отличающиеся друг от друга значительно (орфографически).
- Строки, различающиеся порядком слов.
- Строки, различающиеся количеством слов.
Простота реализации: будет сравниваться сложность процесса сравнения (не буду лукавить, еще до написания функций я понимал, что реализация сравнения по косинусному расстоянию будет немного сложнее, т.к. метрики Левенштейна и Джаро-Винклера работают напрямую со строками, а косинусное расстояние с векторами).
Чтение файла docx
Чуть не упустил один важный момент. Искать подстроку нужно в файле docx, соответственно текст из файла нужно как-то извлечь. С этим поможет библиотека python-docx. Как перевести содержимое файла docx в строку python, ловите код:
import docx
def get_text(filename: str) -> str:
"""Функция извлекает текст из docx файла по указанному пути"""
# создаю объект документа
doc = docx.Document(filename)
# создаю пустой список куда будут помещаться параграфы
fulltext = []
# перебираю все параграфы в документе
for p in doc.paragraphs:
# из каждого параграфа беру текст и добавляю его в список
fulltext.append(p.text)
# соединяю все тексты параграфов в единую строку
return '\n'.join(fulltext)
Об алгоритме поиска подстроки
Сначала на словах об алгоритме поиска похожей подстроки:
- Извлекается текст из файла.
- Используется техника «скользящего окна». «Окно» размером с искомую строку проходит по всему документу и на каждом сдвиге вычисляется метрика (для косинусного сходства на каждом сдвиге нужно еще делать векторизацию).
- Там, где метрика достигла максимального значения, вероятнее всего, находится наша искомая строка.
- В финальной функции нужно установить пороговое значение метрики, чтобы определить, а есть ли вообще искомая строка в документе, но об этом позже, пока нас интересует только скорость выполнения прохода по тексту и расчет метрик.
Код, демонстрирующий реализацию функций для сравнения по скорости, расположен по ссылке в репозитории на github. Ниже представлена таблица сравнения по времени обработки одного документа.
| Косинусное сходство | Сходство Джаро-Винклера | Сходство по Левенштейну |
| 2 m 21 s | 216 ms | 186 ms |
Все-таки в плане производительности с С++ трудно бороться. Джаро-Винклер быстрее косинусного сходства в 652 раза, а Левенштейн в 758. Функцию косинусного сходства нужно сильно оптимизировать, если это вообще имеет смысл. Сильно с выводами торопиться не стоит, у косинусного сходства есть еще туз в рукаве, из сути данной метрики я предполагал, что она должна хорошо отработать случаи, где слова поменяны местами, что получилось в итоге можно посмотреть в таблице ниже.
| Короткие похожие строки | кредитный договор | кридитный дговор |
| Короткие непохожие строки | кредитный договор | костюм деловой |
| Длинные похожие строки | Председатель совета по стандартам бухгалтерского учета избирается на первом заседании совета из представителей субъектов негосударственного регулирования бухгалтерского учета, входящих в его состав. Председатель совета по стандартам бухгалтерского учета имеет не менее двух заместителей. | Предсидатель света по стандартам бугалтерского учета изберается на первом зоседании совета и3 представителей субъектов негосударственного регулирования бухгалтерского учета, входящих в ого состав. Председатель совета по станд@ртам бу%галтерского учета имеет не менее двех заместителей. |
| Длинные непохожие строки | Председатель совета по стандартам бухгалтерского учета избирается на первом заседании совета из представителей субъектов негосударственного регулирования бухгалтерского учета, входящих в его состав. Председатель совета по стандартам бухгалтерского учета имеет не менее двух заместителей. | К основным сведениям об объекте недвижимости относятся характеристики объекта недвижимости, позволяющие определить такой объект недвижимости в качестве индивидуально-определенной вещи, а также характеристики, которые определяются и изменяются в результате образования земельных участков, уточнения местоположения границ земельных участков, строительства и реконструкции зданий, сооружений, помещений и машино-мест, перепланировки помещений. |
| Строки с разным порядком слов (и плохим преобразованием) | К основным сведениям об объекте недвижимости относятся характеристики объекта недвижимости, позволяющие определить такой объект недвижимости | К свебниям основным об объекте относятся \/арактеристики недви%имости недвижимости, позволяющие объекта такой опр$делить объект недвижимости |
| Строки с разным количеством слов | К основным сведениям об объекте недвижимости относятся характеристики объекта недвижимости, позволяющие определить такой объект недвижимости | К сведениям об объекте относятся характеристики объекта недвижимости, позволяющие определить недвижимость |
| Косинусное сходство | Сходство Джаро-Винклера | Сходство по Левенштейну |
| Короткие похожие строки | ||
| 0.942 | 0.899 | 0.909 |
| Короткие непохожие строки | ||
| 0.732 | 0.613 | 0.452 |
| Длинные похожие строки | ||
| 0.999 | 0.905 | 0.971 |
| Длинные непохожие строки | ||
| 0.917 | 0.682 | 0.398 |
| Строки с разным порядком слов | ||
| 0.997 | 0.868 | 0.756 |
| Строки с разным количеством слов | ||
| 0.992 | 0.805 | 0.850 |
Из данной таблицы я сделал следующий промежуточный вывод: косинусное сходство хорошо определяет похожие строки разной длины, с разным порядком слов и даже с пропущенными словами, но есть один неприятный нюанс: чем длиннее сравниваемые строки — тем больше коэффициент косинусного сходства (даже если строки не похожи). Для конкретно моей задачи это может стать определяющим фактором (к слову, Джаро-Винклер и Левенштейн отработали случаи с разным порядком и количеством слов довольно достойно).
В итоге мной было принято решение отказаться от метрики косинусного сходства, и чтобы наглядно продемонстрировать причину данного решения ниже я приведу графики. Это графики обработки одного документа, где по оси х отмечена позиция начала «скользящего окна», а по оси у — метрики.
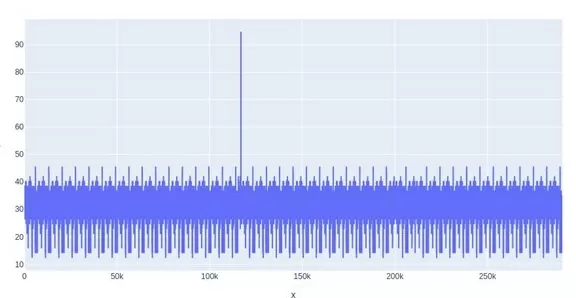
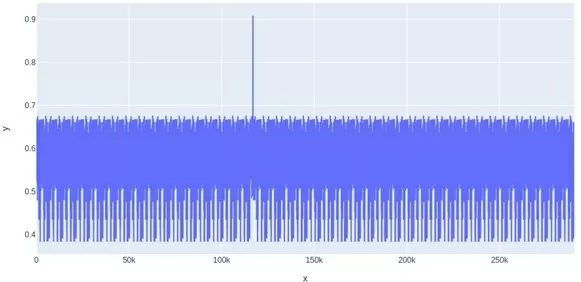
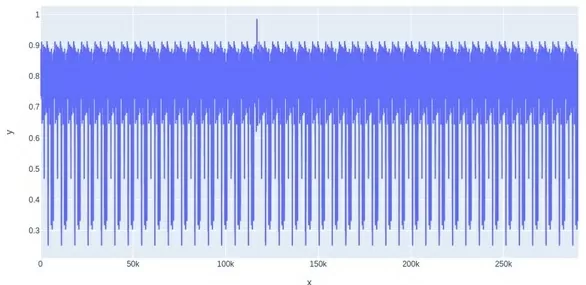
По этим графикам отчетливо видно резкий пик в районе 120 тыс., который указывает на найденную строку, но больше внимания стоит обратить на средний уровень коэффициентов, у косинусного сходства он очень близок к значению, которое соответствует искомой строке. В связи с этим становится затруднительно установить пороговое значение, по которому необходимо определять содержится ли искомая строка в тексте или нет.
Выводы
- Функции, основанные на rapidfuzz работают на порядки быстрее, чем функция, основанная на косинусном сходстве, если необходимо обработать большой пул больших документов, лучше не пользоваться метрикой косинусного сходства.
- Для косинусного сходства сложно эмпирически подобрать порог нахождения подстроки в тексте: особенно если ищем длинную подстроку.
- Косинусное сходство хорошо отрабатывает случаи, когда порядок слов изменен или количество слов в строках отличается, но сходство Джаро-Винклера и Левенштейна отработали не сильно хуже.
- Реализация косинусного сходства немного сложнее из-за дополнительного этапа векторизации.
Итог
В конечном счете выбор сделан в пользу сходства по Левенштейну, с порогом равным 0,7. Библиотека rapidfuzz хорошо показала себя, весь пул входных документов был обработан за 2-3 минуты.
Буду рад, если мои выводы пригодятся для решения и ваших задач!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
