Время прочтения: 5 мин.
Интересно, как много из нас при словах «машинное обучение» и «искусственный интеллект» многозначительно кивают, как бы говоря «да-да, я знаю, мощная штука, нажал кнопку и корабли забороздили космические просторы» или отстранённо машут руками, имея в виду «это какая-то чёрная магия, нам недоступная и мы даже боимся понять её суть». На деле же машинное обучение базируется на законах математики, статистики и т.п., а значит это можно понять или, как минимум, объяснить. Думаю, многие слышали о таком методе машинного обучения, как дерево решений. Действительно, средство крайне эффективное для различных задач классификации и регрессии. А если ещё проще, то дерево решений в одиночку или в совокупности с другими методами подскажет нам выдавать ли кредит, определит стоимость залога, ну или поможет интернет-джину раскрыть загаданного персонажа (но это не точно).
Призываю вас не пугаться формул и расчетов, приведённых ниже – вы точно всё поймёте и раскроете секрет работы одного из методов машинного обучения. Мы будем использовать крайне абстрактный пример, который своим существованием преследует только одну цель: рассказать, как компьютер строит дерево решений. Итак, у нас есть признаки, которые мы знаем о заемщиках:
X1 — Есть ли другие продукты, кроме кредита;
X2 — Выходил ли на просрочку 30+;
А также признак Y (был ли утрачен залог), который нам бы хотелось научиться определять на основании знаний о X1 и X2.
Таблица имеющихся у нас фактов, где 1 – наличие факта, 0 – отсутствие факта:
| X1 | X2 | Y |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 0 | 0 |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 0 | 1 | 1 |
| 0 | 1 | 0 |
Существует несколько вариантов строить дерево, но в данной статье я расскажу об одном – энтропия, в общем понимании — мера хаотичности системы. В нашем случае она принимает значение от 0 (полное отсутствие неопределённости) до 1 (полная неопределённость) и будет показывать, насколько точно мы относим наше наблюдение к определенному классу (Y). Энтропия рассчитывается по формуле:
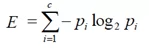
c- число классов, в нашем случае их два (1,0 – утрачен залог или нет).
pi – вероятность отнесения наблюдения к конкретному классу (1,0 – утрачен залог или нет).
Она не так сложна, как кажется. Сейчас мы примерим на себя роль компьютера и построим дерево решений вручную. Для начала считаем энтропию конкретной ситуации:
По искомому столбцу Y – получаем пять значений «1» и пять значений «0»

EY = 1, таким образом мы имеем полную неопределенность.
Как хорошо, что это не все наши данные и у нас есть информация признака X1, так давайте учтём её. Так как у данного признака только два значения (0 и 1), то значением, по которому мы будем разбивать наблюдения будет среднее между ними, а именно 1/2.
Если значение X1>1/2, то при таком условии залог утрачен (Y=1) по 2 наблюдениям и не утрачен (Y=0) также по 2, если X1<=1/2, то залог утрачен (Y=1) по 3 наблюдениям и не утрачен (Y=0) также по 3. Не нужно подставлять в формулу, чтобы понять, что в каждом классе энтропия также равна 1.
Тогда пускаем в бой второй признак.
Если значение X2>1/2, то при таком условии залог утрачен (Y=1) по 4 наблюдениям, а не утрачен (Y=0) по 1, если X2<=1/2, то залог утрачен (Y=1) по 1 наблюдению, а не утрачен (Y=0) также по 4.
Поскольку, мы расплатились по двум классам, наблюдений в каждом получилось по 5. Значит формула примет вид:
Ex2=-4/5*log2(4/5)-1/5*log2(1/5)=0.722. Такой же расчет и для второго класса (=0).
Это уже ниже 1, а значит мы снизили энтропию.
Но как компьютер понимает, какой признак взять для первого разветвления нашего дерева? Он считает Information Gain (IG), выигрыш информации. Формула проста:
IG = E(Y)-E(Y|X)
E(Y) мы уже посчитали на первом этапе, она =1. Для расчета E(Y|X) просто взвешиваем энтропию по наблюдениям, т.е. считаем сколько случаев отнесено к конкретному классу из всех наблюдений и умножаем на их энтропию.
IG для первого признака X1 считается как:
IGx1 = 1 – (4/10 * 1 + 6/10*1) = 0
Для второго X2:
IGx2 = 1 – (5/10 * 0.722 + 5/10*0.722) = 0.278
Таким образом, компьютер выберет разветвление по признаку X2, так как выигрыш информации в данном случае больше. Затем он сделает сплит по переменной X1 и закончит строительство дерева.
Код на Python
import pandas as pd
from sklearn import tree
import graphviz
df=pd. pd.read_csv(file)
X = df[['X1','X2']]
y = df['Y']
clf=tree.DecisionTreeClassifier(criterion='entropy')
clf.fit(X,y)
dot_data = tree.export_graphviz(clf, feature_names=list(X), filled=True,rounded=True)
graph = graphviz.Source(dot_data, format="png")
graph
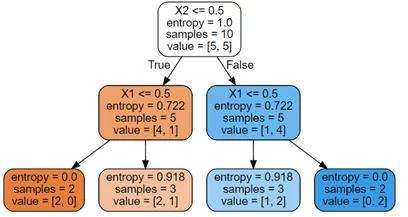
В целом, расчеты не сложные и справиться можно с бумагой и ручкой. А вот когда наблюдений и признаков во много раз больше, тут мы компьютеру не соперники, но алгоритм он будет применять всё тот же: циклично брать признаки, считать энтропию и IG, выбирать признак с наибольшим IG, разветвляться по нему и проделывать заново тоже самое с теми же самыми признаками.
Конечно, этим работа с деревьями не ограничивается, нужно правильно подготавливать данные, контролировать переобучение, анализировать эффективность. Но мы здесь ради сути, и на поверку оказалось, что никакой тёмной магии в алгоритме нет и всё поддаётся восприятию и пониманию. С одной стороны, должно быть радостно, что очередной секрет для нас раскрыт, но с другой стороны как-то грустно, когда фокус раскрывают, весь магический флёр спадает и мы остаёмся один на один с холодной реальностью. А может быть и не нужно всё знать, а иначе, сняв очки, мы обнаружим, что город – то не изумрудный, Гудвин – просто человек, а у Страшилы так и нет мозгов.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
