Время прочтения: 12 мин.
Я надеюсь, что после прочтения этого материала у вас сформируется более глубокое интуитивное понимание самой проблемы, а также вы сможете ориентироваться в методах ее решения и будете лучше понимать, что же сделали или не сделали ваши коллеги, которые разрабатывали модель машинного обучения.
Это особенно важно, поскольку переобучение «коварно», оно может возникнуть неявно и обнаружиться уже когда будет поздно, т.е. уже после внедрения модели в бизнес-процесс, когда ее результаты на новых данных окажутся существенно хуже, чем вы могли видеть во время ее разработки специалистами.
Здесь я постараюсь описать все максимально доступно, но буду рассчитывать, что у читателя есть самые базовые знания в области машинного обучения.
Итак, приступим. Когда я писал выше, что буду изъясняться максимально доступно, я имел ввиду, что буду стараться подбирать аналогии знакомые каждому и по возможности не вводить более строгие математические формулировки. Мне кажется такой подход самым верным, как минимум в рамках данной статьи, поскольку на мой взгляд, именно так оно зачастую и происходит при создании новых понятий и методов.
Математика, как и любая наука, это один из способов формального описания окружающего нас мира, а конкретные ее понятия – это удобные «инструменты» для этого описания.
Для машинного обучения, как для дисциплины из раздела прикладной математики, это работает еще сильнее, поскольку оно изначально создавалось как раз для решения реальных задач. Что особенно интересно, многие методы машинного обучения так или иначе пытаются воссоздать логику человека (почему их и относят к методам искусственного интеллекта), и именно в таком ключе я буду описывать проблему переобучения.
Что такое переобучение?
Многие элементарные для человека задачи очень часто оказываются не столь очевидными для алгоритмов машинного обучения.
К примеру, мы легко можем отличить рыбу от птицы, птицу от млекопитающего и так далее. Можем мы это сделать за счет многих-многих знаний, приобретенных за нашу жизнь, проще говоря в процессе обучения, при этом под обучением тут я имею ввиду вообще любой опыт может быть источником знаний.
На основе этих знаний мы делаем обобщения и, когда увидим животное, которое раньше не встречали, допустим, алмазного фазана, мы легко поймем, что это птица. Мы поймем это по клюву, перьям, ножкам, тому насколько он похож на других птиц и т.д.

Благодаря тому, что мы можем строить такие сложные зависимости, определить, какое животное перед нами для нас не составляет труда.
Но что, если бы мы не могли работать с такими сложными взаимосвязями? Или у нас не было бы такого объема знаний? Или за всю нашу жизнь мы бы видели целую тысячу разных птиц и всего десять собак, как бы тогда мы их отличали друг от друга?
Ровно с такими проблемами сталкиваются модели машинного обучения.
Теперь рассмотрим другой пример, допустим у нас есть данные по некоторым объектам (в нашем случае – опять по животным), под данными я имею ввиду различные признаки, например, вес, окрас, где обитает, что умеет, чем питается каждое животное и так далее.
Наша задача на основе этих данных и собственно разметки (знания, полученного извне или от учителя о том, каким животным является каждый конкретный экземпляр) вывести некое обобщающее правило, которым мы сможем пользоваться в дальнейшем, чтобы уже самостоятельно различать (классифицировать) животных.

Выше изображены и размечены наши объекты, красным – рыбы, зеленым – птицы.
Так как по условию мы изначально ничего не знаем про рыб и птиц, а учимся с нуля, вполне вероятно, что мы выведем правило вроде «кто умеет плавать – тот рыба». И будем в каком-то смысле правы, потому что по такому правилу на этих данных мы не ошибемся ни разу.
Однако, что же произойдет, когда мы встретимся с новым животным и как мы его классифицируем?

Как видим, мы ошибочно определили всех новых животных, но в чем же природа такой ошибки?
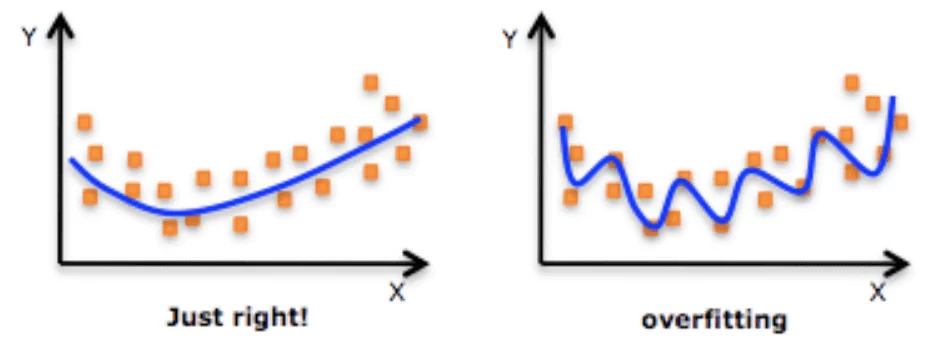
В данном случае очевидно, что мы вывели такое правило, которое имеет место только на обучающей выборке. Такая ситуация и называется проблемой переобучения (overfitting).
Выражаясь чуть более формально, переобучение – это явление, когда качество модели на обучающей выборке существенно превосходит качество модели на тестовой выборке.
И если в данном случае понятно, что изначально было выбрано очень сомнительное правило, то когда счет объектов идет на тысячи, число признаков на десятки или сотни, и при этом реальные модели часто оказываются трудно интерпретируемыми (что вообще говоря, зависит от алгоритма), то переобучение можно заметить, уже только сравнивая качество модели во время обучения и теста.
Подробнее про переобучение и как с ним бороться
«Неправильное» обобщающее правило – довольно общая фраза, на самом деле природа таких «неправильных» правил тоже отличается друг от друга, и в зависимости от нее надо предпринимать соответствующие шаги.
Самый очевидный – увеличить объем обучающей выборки. Для примера выше, если бы у нас были данные не по шести животным, а, скажем, по тысяче (при условии их разнообразия), то мы скорее всего выбрали какое-то более разумное правило, просто потому, что «кто плавает – тот рыба» не работало для некоторых птиц (утках, лебедях и т.д.) уже на этапе обучения, но зато работало бы что-то вроде «у кого жабры – тот рыба».
Опять же, при этом важно разнообразие выборки. Если модель машинного обучения изучит тысячу одинаковых объектов – не стоит ожидать, что ее качество существенно улучшится. Возвращаясь к правилу «кто плавает – тот рыба», будь у нас в обучающей выборке тысяча птиц, но ни одна из них не умела бы плавать – мы бы все равно могли выбрать его.
В общем, данных должно быть много, и они должны быть разнообразными.
Регуляризация
Теперь рассмотрим, пожалуй, основной и самый универсальный метод борьбы с переобучением – регуляризацию.
Для этого представим следующую задачу. Теперь мы в роли судьи и за годы нашего опыта мы придумали строгое правило, по которому можем автоматизированно выносить приговор, для простоты – лишить свободы или оправдать человека (сюда же отнесем условное наказание).
Под строгим правилом мы понимаем чисто математическое выражение приговора через какие-то факты, и если сумма этих фактов больше определенного порога (для простоты — 50), то будем считать человека виновным.
Это может выглядеть так:
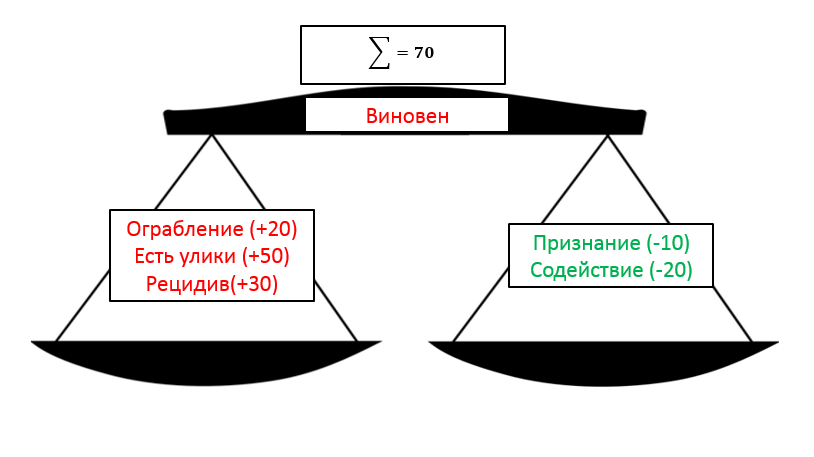
Т.е. подсудимый совершил ограбление, найдены улики, к тому же он рецидивист. При этом есть некоторые смягчающие обстоятельства, но их веса недостаточно, чтобы оправдать или отделаться условным сроком:
20+50+30-10-20=70>50⇒Виновен
Теперь представим, что за все время работы судьей мы ни разу не оправдали/не давали условный срок по делам кражи. Тогда модель машинного обучения может решить, что любой обвиняемый по делу кражи, т.е. факту обвинения в краже будет дан такой большой вес, что все остальные факты окажутся незначительными, например, как на рисунке ниже.
Фактически мы понимаем, что при отсутствии улик, показаний свидетелей и т.п. мы не сможем осудить человека. Но, повторюсь, ранее по всем делам кражи подсудимые были признаны виновными. Т.е. у нас просто нет опыта, который бы подтвердил такую логику.
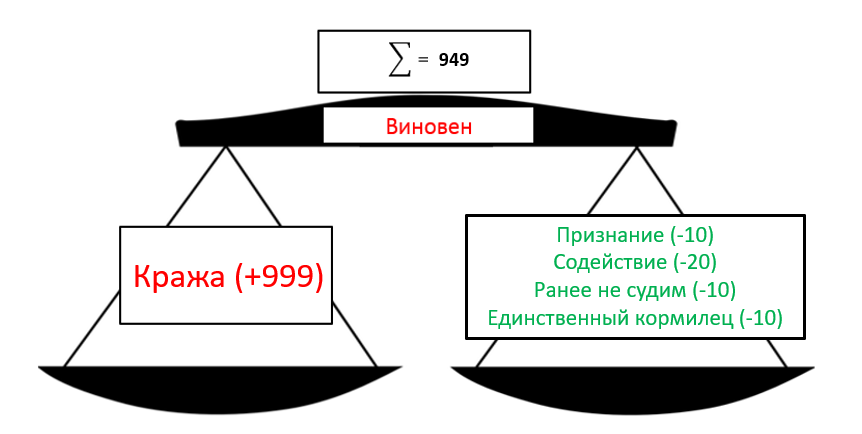
К счастью, как раз для таких случаев существует регуляризация – метод, который не позволяет отдельным фактам/признакам получать слишком большие веса.
Чтобы лучше понять, что это значит, уточним, на что ориентируется модель, когда обучается.
Модели машинного обучения в процессе обучения всегда делают одно – минимизируют свои ошибки на обучающей выборке. Говоря точнее, минимизируют даже не ошибки, а функцию потерь – некоторое количественное выражение допущенных ошибок.
Чем больше ошибок – тем больше значение функции потерь.
Когда мы добавляем регуляризацию – наша функция потерь меняется, теперь важны не только ошибки, но и веса отдельных фактов/признаков, на которые мы опираемся, причем, чем больше веса – тем больше значение функции потерь.
Формально, без регуляризации имеем следующую функцию потерь:
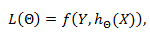
Где L– функция потерь, которая зависит от весов ;
f– просто некоторая функция, которая дает количественное выражение совершенных ошибок;
Y – целевая переменная, в данном примере – «виновен» или «невиновен»;
h (x)– это собственное наше обобщающее правило, которая при определенных весах выражает целевую переменную через набор фактов/признаков .
С регуляризацией — такую:
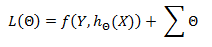
То есть, теперь мы учитываем сумму всех весов.
Примечание: фактические берется немного другая сумма, но не будем излишне усложнять, поскольку смысл этого слагаемого не меняется – мы «штрафуем» модель за слишком большие веса.
Что получаем? Вспомним условие примера с кражей – на нашем опыте по всем кражам подсудимые были признаны виновными. До этого сам факт кражи уже был достаточным для того, чтобы посадить подсудимого, по крайней мере так считала модель. Но если мы введем регуляризацию, модель не сможет так «сжульничать», выбрав слишком простое обобщающее правило (на самом деле может быть и наоборот, когда модель выбирает слишком «сложное» правило), и будет вынуждена искать более сложные (или наоборот, более простое). Однако, скорее всего возрастет и ошибка, но в любом случае рассмотрим, как это можем выглядеть:
| Модель | f (Y, h (x)) | | |
| С большими весами | 0 | 1000 | 1000 |
| С небольшими весами | 100 | 100 | 200 |
То есть, несмотря на то что модель с небольшими весами ошибается больше, общее значение функции потерь оказывается меньше, а значит, модель с небольшими весами окажется предпочтительнее.
Соответственно, веса примут примерно такие значения, и мы вынесем следующий приговор:
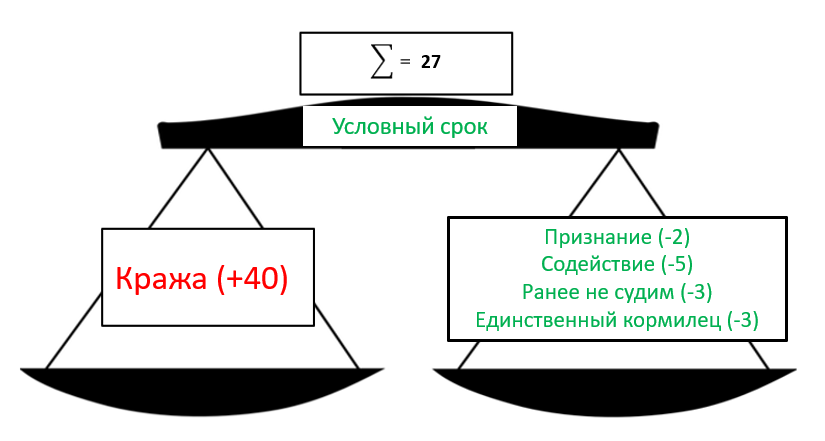
Проще говоря, регуляризация «заставляет» модель искать более взвешенные решения, а не основанные на одном-двух признаках. Как и мы, модель с регуляризацией старается принимать решения, учитывая все возможные факторы и не упускать ничего из виду.
Пример
Теперь попробуем показать более конкретный случай. Задача сделана по мотивам одного из уроков курса mlcourse.ai Юрия Кашницкого, который в свою очередь ссылается на Стэнфордский курс по машинному обучения от Andrew Ng.
В этой задаче у нас есть массив данных для 118 микрочипов, два признака – тест 1 и тест 2. По результатам этих двух тестов принимается решение браковать или выпускать очередной микрочип – это и есть наша целевая переменная, то есть мы решаем задачу бинарной классификации.
Поскольку у нас всего два признака, очень просто будет визуализировать наши данные.
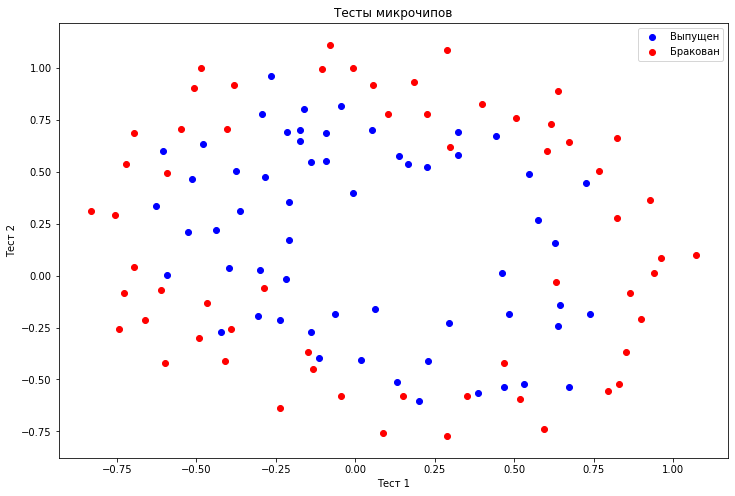
Важное примечание, тут признаки уже центрированы (т.е. из них вычли среднее значение соответствующего признака по всем объектам).
Что же от нас требуется? Нам надо каким-то образом, основываясь на данных двух признаках научится отличать «красные» точки от «синих». Результатом этого будет какое-то правило «разделяющее» точки между собой. Это правило так и называется – «разделяющая гиперплоскость» и выглядит примерно так:
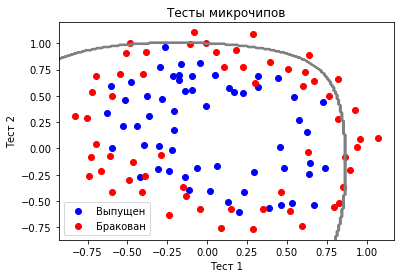
То есть для двумерного признакового пространства – это просто прямая.
Это пример плохой модели, которая разделяет точки неправильно. Немного ее улучшив (использовав полиномиальные признаки), мы получим что-то вроде такого:
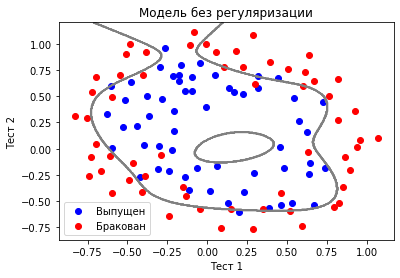
Мы видим, что новая линия намного лучше разделяет точки, но возникает другая проблема. Если бы мы могли просто нарисовать эту линию рукой, мы бы скорее всего нарисовали овал или круг, но линия, построенная моделью, оказалась куда более сложной. То, что модель вывела такие «слишком» сложные закономерности в данных, говорит о том, что она переобучилась.
Теперь посмотрим, что будет, если мы воспользуемся регуляризацией:
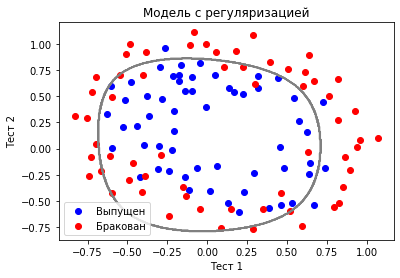
Вот это уже больше похоже на правду. Хотя с виду модель, кажется, ошибается больше, но теперь у нас не возникает сомнений в «адекватности» правила, которое она выводит.
Теперь то, о чем мы говорили до этого чисто теоретически рассмотрим на этом примере.
Во-первых, мы говорили, что переобученная модель ищет слишком простое или, наоборот, слишком сложное правило – главное, что «слишком». На языке модели это значит, что она дает отдельным признакам слишком большие веса, при построении прогноза. Если мы будет сравнивать веса модели «без» и «с» регуляризацией, то мы увидим следующую картину:
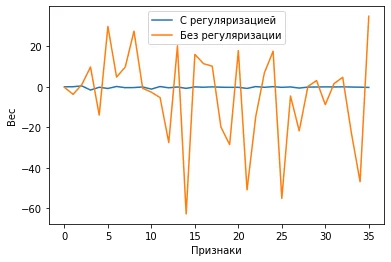
Примечание: может возникнуть вопрос – откуда столько признаков? Как мы упомянули ранее, мы использовали полиномиальные признаки (7-й степени), что дает нам суммарно 36 признаков.
Веса признаков с регуляризацией как правило не больше +/- единицы, в то время как веса признаков без регуляризации сильно разбросаны, но в основном они выходят далеко за пределы единичного круга.
И последнее, я уже показывал, как может выглядеть выбор лучшей модели с учетом регуляризации «по идее», посмотрим, что получилось на практике и сравним эти две:
| Модель | f (Y, h (X) | | |
| Без регуляризации | 32,30 | 141,49 | 173,78 |
| С регуляризацией | 65,56 | 2,75 | 68,31 |
Хотя модель без регуляризации меньше ошибается (значение функционала ошибки во втором столбце), разница в весе признаков оказывается более существенной, поэтому модель с регуляризацией для нас будет предпочтительнее.
Заключение
В заключение надо сказать, что, конечно, существуют и другие, специфичные для конкретных алгоритмов машинного обучения способы борьбы с регуляризацией, но эти являются, пожалуй, основными и самыми универсальными.
Надеюсь, я помог вам интуитивно понять — что же такое проблема переобучения, от чего зависит и к чему приводит, и как мы можем с этим бороться.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)