Время прочтения: 10 мин.
В качестве первой задачи для машинного обучения возьмем что-то понятное и простое, например, прогноз стоимости жилья. Готовый датасет можно найти на сайте kaggle. На первых шагах обучения не стоит брать датасеты с большим количеством переменных, например, «House Prices: Advanced Regression Techniques» состоит из 80 переменных и advanced regression, остановимся на «House Sales in King County, USA» с 21 параметром. Скачиваем данные и анализируем предоставленное описание. В наличии дата, цена, количество спален, ванных комнат, общая и жилая площадь, этажность, оценка вида, вид на море, оценка общего состояния, грейд (оценка строительства и дизайна), площадь над и под уровнем земли, год постройки, год последнего ремонта, код зоны, координаты (долгота и широта), данные о площади домов 15 соседей.
Итак, мы выбрали задачу и готовы приступить к ее решению. Решение будет включать два этапа: анализ данных и построение моделей.
1. Работа с данными.
Сделаем отступление и отдельно отметим важность анализа данных. В настоящий момент все более-менее популярные алгоритмы уже написаны в виде библиотек и непосредственное построение модели сводится к нескольким строкам кода, например, k-ближайших соседей из sklearn в python:
from sklearn .neighbors import KNeighborsClassifier
clf_KNN = KNeighborsClassifier() #Создаем модель
clf_KNN.fit(X_train, Y_train) #Обучаем модель
Y_KNN = clf_KNN.predict(X_test) #Предсказываем значения для выборки Всего четыре строчки кода для получения результата. Так в чем же сложность? Сложность заключается в получении того самого X_train – данных, которые подаются на вход модели. Известный принцип «мусор на входе» = «мусор на выходе» (Англ. Garbage in – garbage out (GIGO)) в моделировании работает более чем на 100% и именно от работы с данными во многом будет зависеть качество полученного решения задачи машинного обучения.
А теперь – в бой!
Для анализа данных мы будем использовать pandas, для понимания и оценки «на глаз» используем простые графики из seaborn.
Импортируем библиотеки, читаем данные, выведем несколько записей из массива данных, посмотрим на типы данных и пропуски в них.
Код и Out
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv('…/train.csv')
df.head(5)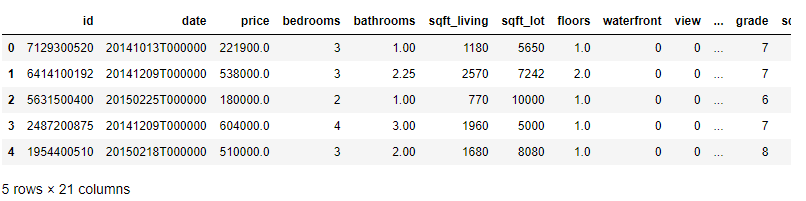
df.info() RangeIndex: 21613 entries, 0 to 21612
Data columns (total 21 columns):
id 21613 non-null int64
date 21613 non-null object
price 21613 non-null float64
bedrooms 21613 non-null int64
bathrooms 21613 non-null float64
sqft_living 21613 non-null int64
sqft_lot 21613 non-null int64
floors 21613 non-null float64
waterfront 21613 non-null int64
view 21613 non-null int64
condition 21613 non-null int64
grade 21613 non-null int64
sqft_above 21613 non-null int64
sqft_basement 21613 non-null int64
yr_built 21613 non-null int64
yr_renovated 21613 non-null int64
zipcode 21613 non-null int64
lat 21613 non-null float64
long 21613 non-null float64
sqft_living15 21613 non-null int64
sqft_lot15 21613 non-null int64
dtypes: float64(5), int64(15), object(1)
memory usage: 3.5+ MB
Массив данных состоит из 21613 записей без пропусков в данных и содержит только 1 текстовое поле date.
С каждым признаком поработаем подробнее и начнем с самого простого – откинем id (не несет полезной информации), zipcode (код зоны, где расположен дом) и координаты (lat & long), так как мы только знакомимся c machine learning, а корректное преобразование географических данных слишком специфично для начинающего специалиста.
df=df.drop(['id','zipcode','lat','long'], axis=1)Теперь посмотрим на дату объявления. Формат даты задан YYYYMMDDT000000, в целом ее тоже можно было бы удалить из датасета, но у нас есть поля год постройки (yr_built) и год последнего ремонта (yr_renovated), которые заданы в в формате года (YYYY), что не очень информативно. Оперируя датой объявления можно преобразовать год в возраст вычитанием (год объявления — год постройки / год ремонта). Отметим по части домов год ремонта стоит 0, и, предположив, что это означает отсутствие ремонта с постройки, заменим нули в году ремонта на год постройки, предварительно убедившись, что в данных отсутствуют некорректные записи, где год ремонта меньше года постройки:
df[(df['yr_renovated']<df['yr_built'])&df['yr_renovated']!=0]
df.loc[df['yr_renovated']==0, ['yr_renovated']]=df['yr_built']
df['yr_built']=df['date'].str[0:4].astype(int)-df['yr_built']
df['yr_renovated']=df['date'].str[0:4].astype(int)-df['yr_renovated']
df=df.drop('date', axis=1)
df.head(5)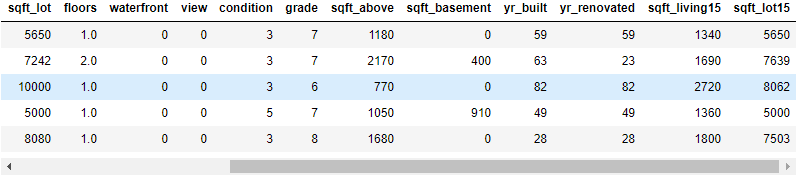
Следующим параметром проанализируем цену и воспользуемся для этого «Ящиком с усами» (Box plot). Ящик с усами – простой и удобный график, показывающий одномерное распределение вероятностей, или, проще говоря, концентрацию данных. Отрисовывает медиану (линия в центре), верхний и нижний квартили (стороны ящика), края статистически значимой выборки («усы») и выбросы (точки за «усами»). Легко понять по картинке на нормальном распределении (справа). График позволяет быстро оценить где располагается большая часть данных (50% находятся внутри ящика), их симметричность (смещение медианы к одной из сторон ящика и/или длина «усов») и степень разброса – дисперсию (размеры ящика, размеры усов и количество точек-выбросов).
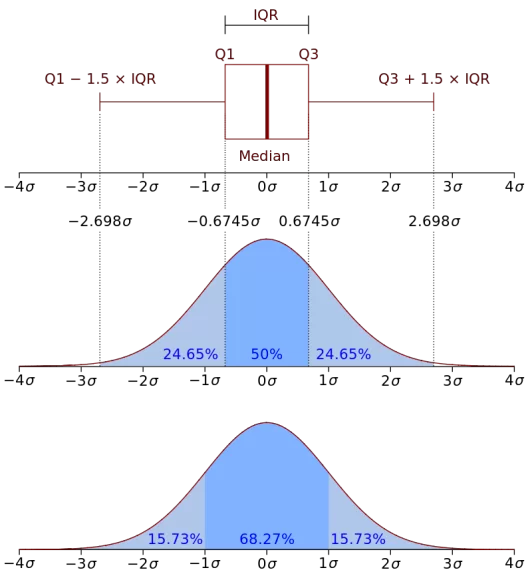
Можно построить распределение только этого признака по всему массиву, но информативнее будет использовать 2оси – например, цену и количество спален, что в свою очередь также покажет наличие связи между признаками:
sns.boxplot(y='price', data=df) #только price
sns.boxplot(y='price', x='bedrooms', data=df) #price & bedroomsOut price & bedrooms:
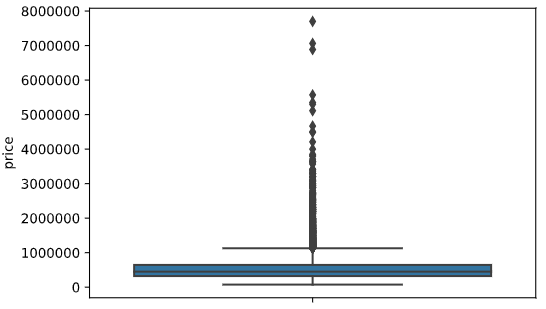
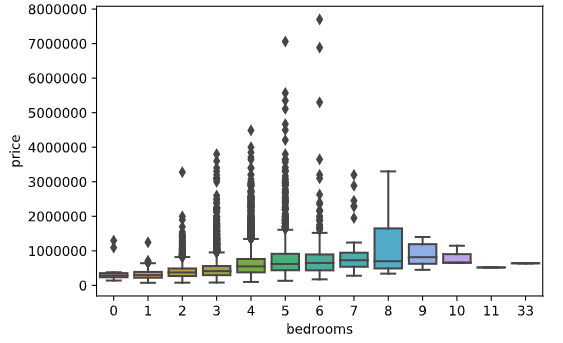
Из графика сразу видно наличие экстремальных значений price и bedrooms (только представьте дом с 33 спальнями! J). Наличие таких значений (иначе называемых как выбросы) в целевом признаке price часто приводит к переобучению модели, так именно они будут давать большую ошибку, которую алгоритмы стараются минимизировать. Из графика видно, что большая часть (если посчитать – 93,22%) лежит в диапазоне 0-1млн, а свыше 2млн – всего 198 значений (0,92%). От 1% датасета можно избавиться практически безболезненно, поэтому вызвав простой просмотр 217 записей предварительно отсортировав по цене, увидим искомую отметку price в 1 965 000 и удалим все что выше этой цены.
df.sort_values (by='price', ascending=False).head(217)
df=df[df['price']<=1965000]Подумаем немного над признаком bedrooms. Мы видим 13 домов с bedrooms = 0, а также странную запись о доме с 33 bedrooms. Поступим также как и с price, удалив нули из bedroms (а заодно и bathrooms):
df=df[(df['bedrooms']!=0)&(df['bathrooms']!=0)]Касательно дома с 33 спальнями – учитывая цену, можно предположить что это опечатка и спален на самом деле 3. Сравним жилую площадь этого дома (1620) со средней жилой площадью домов с 3 спальнями (1798,2), что ж вероятно наша догадка верна, поэтому просто изменим это значение на 3 и еще раз построим предыдущий box plot:
df.loc[df['bedrooms']==33,['bedrooms']]=3
sns.boxplot(y='price', x='bedrooms', data=df)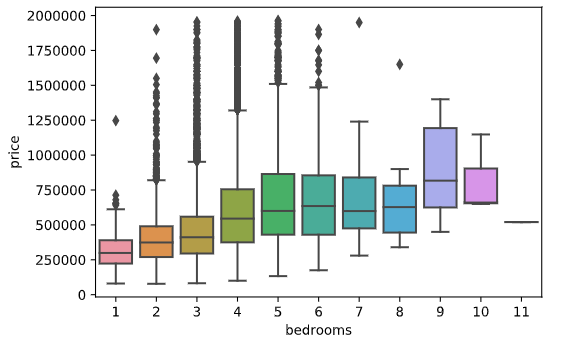
Чтож, значительно лучше. Аналогично bedrooms посмотрим и на bathrooms. Нулевые значения мы удалили, другие экстремальные значения в поле отсутствуют:
sns.boxplot(y='bathrooms', x='bedrooms', data=df)В полях sqft_living, floors, waterfront, view, condition, grade, sqft_living15 также все значения более-менее реальны, их трогать не будем:
plt.rcParams['figure.figsize']=2,3 #размер картинки
sns.boxplot(y='sqft_living', data=df)
sns.boxplot(y='floors',color='#2ecc71', data=df)
sns.boxplot(y='sqft_living15',color='#9b59b6', data=df)
plt.rcParams['figure.figsize']=4,4
sns.boxplot(y='price', x='waterfront', data=df)
sns.boxplot(y='price', x='view' , data=df)
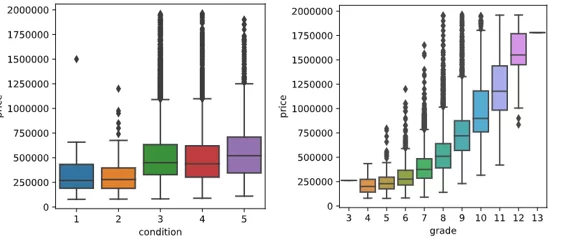
sns.boxplot(y='price', x='condition' , data=df)
sns.boxplot(y='price', x='grade' , data=df)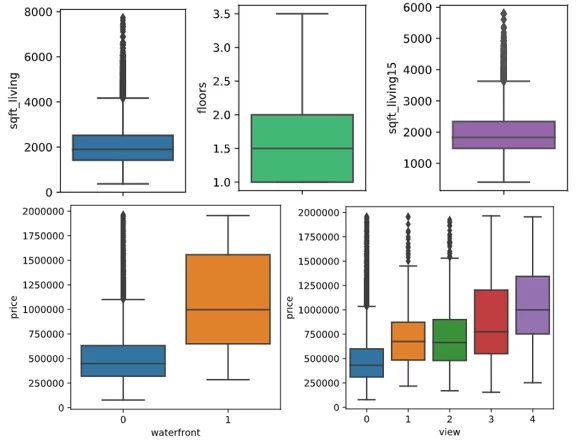
А вот с sqft_lot и sqft_lot15 нужно что-то придумать и из-за больших значений вполне подойдет логарифмирование:
df['sqft_lot']=np.log(df['sqft_lot'])
df['sqft_lot15']=np.log(df['sqft_lot15'])sqft_lot до и после:
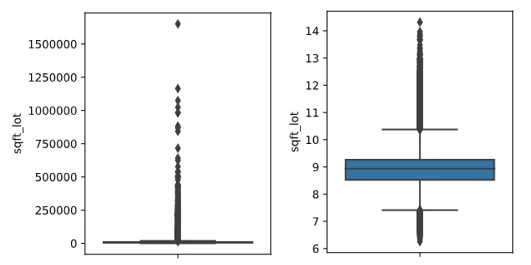
sqft_above и sqft_basement – составные части sqft_living, поэтому также трогать их не будем.
На этом с предварительным анализом мы закончим и посмотрим на тепловую карту корреляций:
sns.heatmap(df.corr(), cmap = 'viridis',annot = True)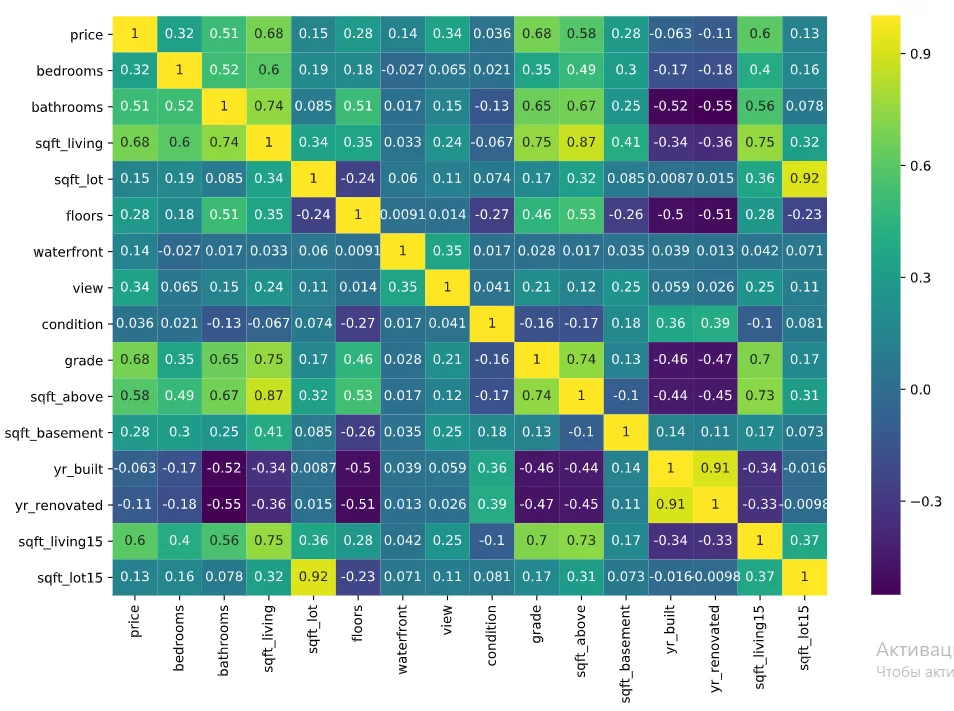
Изучив карту корреляций видим, что иногда признаки сильно коррелированы между собой, поэтому удалим часть признаков с высокой корреляцией – sqft_lot15 (оставим sqft_lot), yr_built (оставим yr_renovated), sqft_above (sqft_living)
На этом закончим работу с данными и перейдем к созданию модели.
2. Моделирование
В данной части мы построим 2 модели: линейную регрессию и дерево решений.
Все необходимые нам модели содержаться в библиотеке sklearn.
Для начала отделим целевую переменную от остальных данных для обучения, а также разделим выборки на обучающую (70%) и тестовую (30%, на которой мы проверим как работает модель):
Y=df['price']
X=df.drop ('price',axis=1)
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.3, shuffle = True)Также из sklearn для оценки модели загрузим 3 метрики — mean_absolute_error (средняя абсолютная ошибка), mean_squared_error (Среднеквадратическое отклонение), r2_score (коэффициент детерминации):
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_scoreНачнем с линейной регрессии:
from sklearn.linear_model import LinearRegression
LR = LinearRegression() #Создаем модель
LR.fit(X_train, Y_train) #Обучаем модель
Y_LR = LR.predict(X_test) #Предсказываем значения для выборки
print ('MAE:', round (mean_absolute_error(Y_test, Y_LR),3)) #Метрики
print ('√MSE:', round (mean_squared_error(Y_test, Y_LR)**(1/2),3))
print ('R2_score:', round (r2_score(Y_test, Y_LR),3))MAE: 124477.452
√MSE 175205.645
R2_score: 0.627
Дерево решений:
from sklearn.tree import DecisionTreeRegressor
TR = DecisionTreeRegressor() #Создаем модель
TR.fit(X_train, Y_train) #Обучаем модель
Y_TR=TR.predict(X_test) #Предсказываем значения для выборк
print ('MAE:', round (mean_absolute_error(Y_test, Y_TR),3)) #Метрики
print ('√MSE:', round (mean_squared_error(Y_test, Y_TR)**(1/2),3))
print ('R2_score:', round (r2_score(Y_test, Y_TR),3))MAE: 151734.906
√MSE 220856.721
R2_score: 0.407
Исходя из метрик можно сделать вывод о том, что Линейная регрессия показала лучший результат, поэтому логичнее выбрать ее. Однако, мы не задавались вопросами из чего состоит ошибка модели, не является ли модель переобученной, и пр. Вполне вероятно, что к ухудшению результата DecisionTreeRegressor приводит именно переобучение, так как мы даже не ограничивали глубину дерева в параметрах модели. Можем легко проверить это перебрирая глубину деревьев в коротком цикле:
dep,score=[],[]
for i in range(3,16):
TR = DecisionTreeRegressor(max_depth=i)
TR.fit(X_train, Y_train)
Y_TR=TR.predict(X_test)
dep.append(i)
score.append(mean_squared_error(Y_test, Y_TR)**(1/2)) #Массив значений √MSE
plt.rcParams['figure.figsize']=6,3
plt.plot(dep, score)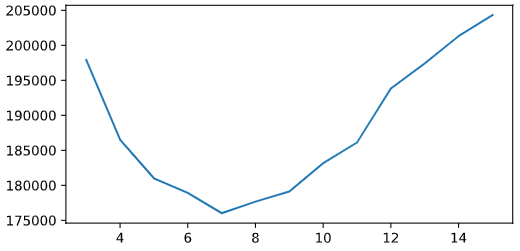
Очевидно, что лучший показатель при max_depth=7, и, посмотрев, на метрики (MAE: 124861.441, √MSE 175322.737, R2_score: 0.626) становиться понятно, что модель с таким ограничением аналогична линейной регрессии по качеству.
Также мы можем попробовать оценить какие признаки оказались наиболее важны для модели для прогноза стоимости:
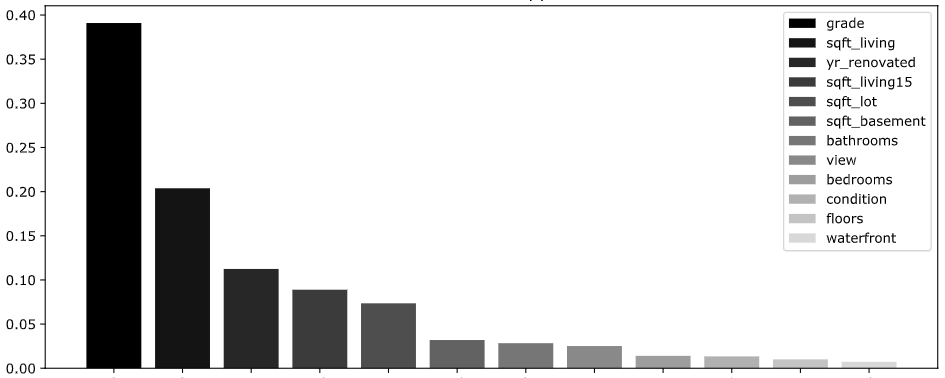
Исходя из графика видно, что на стоимость больше всего влияет grade – общая субъективная оценка дома риелторской компанией (что, кстати, говорит о компетентности оценки :-))), на втором месте – площадь дома, а на третьем – год последнего ремонта. Показатели количества спален, ванных комнат, этажей же модель посчитала незначимыми для прогноза.
Для лучшего понимания результатов, посчитаем среднюю ошибку в % — по линейной регрессии средняя ошибка 27,5%, то есть модель ошибается чуть больше, чем на четверть при прогнозе стоимости дома, что довольно много.
Можно ли улучшить результаты? Да, несомненно, на текущем этапе мы получили только базовое решение – некую отправную точку для сравнения лучше или хуже будут модели, которые мы можем создать более сложными методами или применяя более сложную обработку данных.
Мы только чуть-чуть затронули вопрос переобучения и совсем не прикасались к тому, из чего состоит ошибка модели и многим другим аспектам создания модели. Как правило, для ответов на эти вопросы и нахождения оптимального решения используют разнообразные методы валидации моделей, но об этом мы напишем в следующих статях.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
