Время прочтения: 5 мин.
Анализ данных сам по себе не всегда является самой сложной и затратной задачей. Однажды мне приходилось применять методы Process Mining, при чем сам Process Mining сам по себе был более простым упражнением. При анализе данных очень часто стоит вопрос выгрузить их из различных источников и затем обработать. На словах это может звучать очень просто, но обработка данных иногда заставляет поломать голову, чтобы найти лучшее решение. Тут то и может пригодится знание алгоритмов и структур данных.
Пример. В достаточно крупных организациях используют принцип ITSM (IT Service Management, управление ИТ-услугами). Одним из ключевых концептов такого подхода является управление инцидентами. Первая цель такого управления — это восстановление работоспособности сервиса как можно быстрее. Инциденты могут быть как одиночными, так и связанными. Интересно рассматривать инциденты в связке. Обычно есть какая-то таблица взаимосвязей, в которой указана ссылка на предыдущий инцидент. Для дальнейшего анализа нужно найти все такие связки.
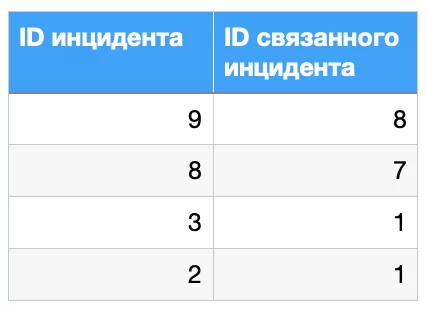
Ситуация усложняется, если связь между инцидентами дополнительно указывается где-то неявно в текстовых полях. Получается несвязный граф, вершинами которого являются ID инцидента, а ребра означают связь между инцидентами. Вызовом становится не только вопрос эффективности, но и просто безошибочная реализация. Есть структура данных, которая идеально подходит для подобного рода задач, и она называется система непересекающихся множеств.
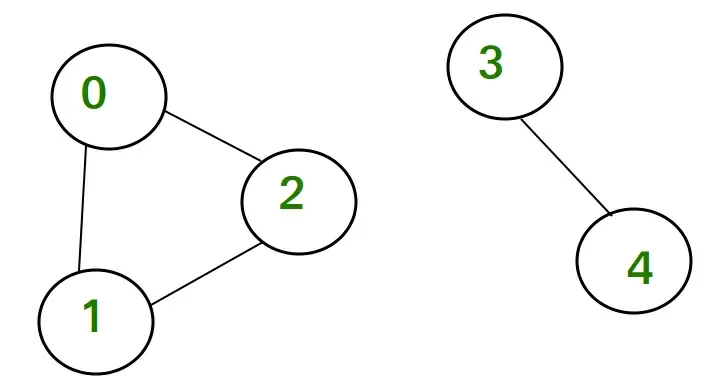
Система непересекающихся множеств (англ. disjoint set) – это структура данных, которая поддерживает множество элементов, разделенное на некоторое количество непересекающихся подмножеств. В каждом подмножестве существует представитель. Такие подмножества – это есть набор деревьев, корнем в которых и будет их представитель.
Такая структура данных поддерживает следующие методы:
- make_set(x) – создает для элемента х новое подмножество. Назначает этот же элемент представителем данного подмножества.
- union(l, r) – объединяет оба подмножества, принадлежащие представителям l и r. Назначает один из них представителем.
- find(x) – определяет для х подмножество, к которому принадлежит элемент, и возвращает его представителя.
Получается, чтобы проверить, принадлежат ли инциденты к одной связке, достаточно проверить, если у них один и тот же представитель. У каждого элемента мы должны знать его родителя и в эффективных алгоритмах глубину дерева для того, чтобы при объединении двух подмножеств более маленькое дерево подвешивалось к корню более глубокого дерева. Ключевая особенность этого алгоритма в том, что каждый раз, когда мы хотим узнать представителя, мы поднимаемся вверх, и по пути собираем все элементы и переподвешиваем их к корню нашего дерева(подмножества).
На рисунке ниже показана операция find для элемента с номером 7. Представитель в этом множестве – это 1. По пути до корня, мы будем вынуждены посмотреть элементы 5, 3 и 2. Чтобы этот проход не прошел понапрасну, элементы 7, 5 и 3 переподвешиваются к корню, так, что в следующий раз до него дойти гораздо быстрее.
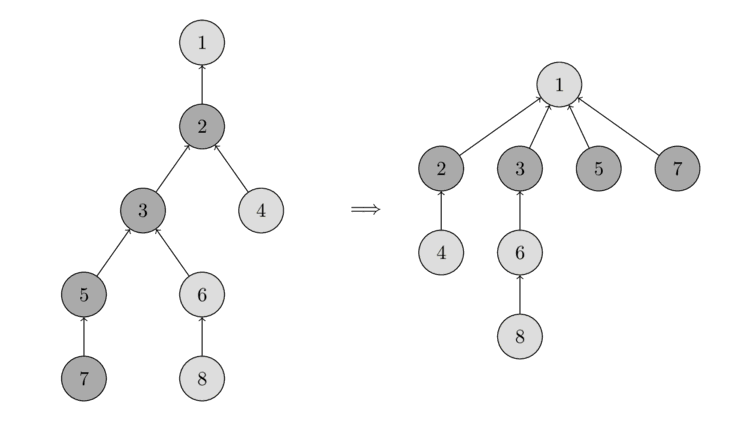
Амортизационная сложность операций find и union O(log*(n)), где log*(n) – это итерированный логарифм. Функция, растущая настолько медленно, что на практике ее значение не превосходит значение 5. То есть можно считать, что сложность будет О(1).
Писать с нуля эту структуру данных не обязательно. Она достаточно распространенная и уже реализована, например, на Python. Для ее использования достаточно установить библиотеку disjoint_set с помощью командной строки и дальше применять 3 стандартных метода.

Ниже приведены наглядные примеры использования библиотеки.
>>> from disjoint_set import DisjointSet
>>> ds = DisjointSet()
>>> ds.find(1)
1
>>> ds.union(1,2)
>>> ds.find(1)
2
>>> ds.find(2)
2
>>> ds.connected(1,2)
True
>>> ds.connected(1,3)
False
>>> "a" in ds
False
>>> ds.find("a")
'a'
>>> "a" in ds
True
>>> list(ds)
[(1, 2), (2, 2), (3, 3), ('a', 'a')]
>>> list(ds.itersets())
[{1, 2}, {3}, {'a'}]
Вернемся к исходной задаче. Для построения всех связок инцидентов, нам нужно добавлять в несвязный граф ребра (связи между инцидентами) одно за другим. Таким образом граф постоянно растет, связные компоненты нужно постоянно наращивать. А делать это эффективно как раз и позволяют непересекающиеся множества.
Создадим инциденты
import numpy as np
NUM_INCIDENTS = 1000 ** 2
NUM_RELATIONS = NUM_INCIDENTS // 2
incidents = [f'id{i:06}' for i in range(NUM_INCIDENTS)]
incidents[:5]
Создадим таблицу взаимосвязей
import pandas as pd
np.random.seed(42)
relations = pd.DataFrame()
relations['id'] = incidents
depend = np.random.choice(incidents, size=NUM_RELATIONS)
depend = np.hstack([depend, incidents[depend.shape[0]:]])
relations['depend'] = depend
relations.head()

Объединение в кейсы
%%time
from disjoint_set import DisjointSet
ds = DisjointSet()
for id_, depend in relations.values:
ds.union(id_, depend)
caseid = [ds.find(id_) for id_ in relations['id'].values]
relations['caseid'] = caseid
relations.head()

Вот и все. Миллион записей обработались всего лишь за 10 секунд на обычном ноутбуке. Теперь можно строить граф процесса.
В целом, это всего лишь один пример, когда непересекающиеся множества позволили эффективно находить связки инцидентов. Такая структура данных также является ключевым компонентом в алгоритме Крускала (для нахождение минимального остовного дерева). Да и, вообще, я призываю вас смотреть немного шире. Вместо инцидентов могло быть, что угодно. Эта структура полезна всегда, когда нужно отслеживать связные компоненты в ненаправленном графе и проверять являются ли 2 вершины частью чего-то большего. Если граф растет, а связные компоненты нужно постоянно обновлять (при условии, что не нужно ничего удалять), то можно обратиться к этой структуре данных.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
