Время прочтения: 6 мин.
Перед нами стояла задача выявления групп клиентов, имеющих одинаковое инвестиционное поведение при совершении операций на организованных рынках ценных бумаг.
Для результативного решения задачи в первую очередь необходимо определиться с ее правильной постановкой.
Итак, в наличии у нас есть датасет по операциям клиентов на фондовом рынке. Сам датасет огромный и находить в нем информацию «вручную» или даже с помощью агрегации сложно и неэффективно. Исходя из этого определяем нашу первую цель – уменьшение датасета, выбрав из всех данных только самые схожие. Кроме того, нет смысла рассматривать схожие операции одного клиента, следовательно, это тоже надо предусмотреть. Собственно, можно начинать!
Фичи, по которым мы будем сравнивать и искать схожие операции:
- время проведения операции,
- инструмент (вид ценной бумаги)
- тип операции (покупка/продажа).
Так как у нас 2 переменные будут категориальными, то, с учетом нашей задачи, будущая модель будет искать близкие по времени операции одного типа, но разных клиентов. Для упрощения дальнейшей работы с данными – вполне подходит!
После загрузки визуализация распределения всех данных выглядит следующим образом:
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection = '3d')
ax.scatter3D(X[:,0],X[:,1],X[:,2])
plt.show()
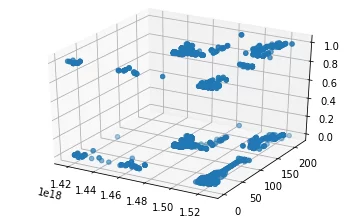
Для проведения анализа мы рассмотрели 2 модели библиотеки SKlearn и одно решение предложили без применения ML – необычное использование метода KMeans, метод DBSCAN и нахождение ближайших соседей (расстояния) для каждой точки в наборе данных с помощью BallTree.
DBSCAN
DBSCAN (Density-based spatial clustering of applications with noise), плотностной алгоритм пространственной кластеризации с присутствием шума), как следует из названия, оперирует плотностью данных. На вход он просит уже знакомую матрицу близости и два загадочных параметра — радиус ϵ-окрестности и количество соседей. Так сразу и не поймёшь, как их выбрать, причём здесь плотность, и почему именно DBSCAN хорошо расправляется с шумными данными? Без этого сложно определить границы его применимости.
После применения метода к нашим данным получаем следующую картину:
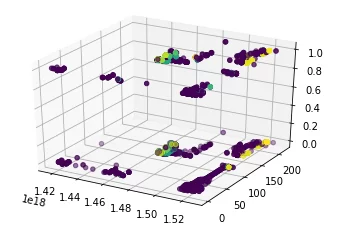
Далее, нам остается сгруппировать данные по лейблу и коду клиента, после чего найти строки, где модель нашла совпадение и убрать среди них строки с одним и тем же кодом клиента. После чего, записываем итоговые данные в лист, получая такой набор схожих кодов клиентов:
X = df[['ORDERDATETIME','SECURCODE','OPERATION']].values
model = DBSCAN(min_samples=2, eps = 0.5).fit(X)
df['LabelsDBS'] = model.labels_
df['ORDERDATETIME']=pd.to_datetime(df['ORDERDATETIME'])
gr=df.groupby(['LabelsDBS','CLIENTCODE']).count()
l=[]
ll=[]
for i in range(gr.shape[0]):
l.append(gr.index[i][0])
ll.append(gr.index[i][1])
l=pd.DataFrame(l)
l.rename(columns={0:'Ind'}, inplace=True)
l['Code']=ll
l=l.query('Ind > 0')
a = l.groupby('Ind').count()
a=a.query('Code>1 & Code<4').index.values
a=list(a)
l=l.query('Ind == @a')
l = pd.DataFrame(l.groupby('Ind')['Code'].apply(list))
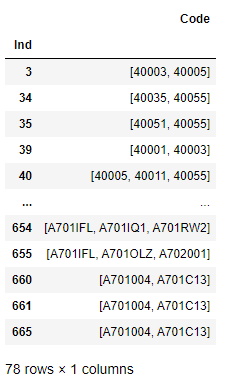
Хочется отметить, что основными недостатками DBSCAN является неспособность соединять кластеры через проёмы, а также способность связывать явно различные кластеры через плотно населённые перемычки.
KMeans
В алгоритме метода k-средних есть два основных этапа. Сначала мы выбираем k разных центров кластеров – как правило, это просто случайные точки в наборе данных. Затем мы переходим к нашему основному циклу, который также состоит из двух этапов.
Первый – это выбор, к какому из кластеров принадлежит каждая точка из X. Для этого мы берём каждый пример и выбираем кластер, чей центр ближе всего.
Второй этап – заново вычислить каждый центр кластера, основываясь на множестве точек, которые к нему приписаны. Для этого берутся все соответствующие примеры и вычисляется их среднее значение, отсюда и название метода – «метод k-средних».
Мы можем догадаться, что для модели идеальным решением будет, когда k-центров будет равно n-точек и расстояние от каждого центра до каждой точки будет равно 1. Именно к такому состоянию стремится модель. Т.е. мы можем предположить, что если мы возьмем количество кластеров чуть меньше количества точек, то наша модель объединит лишь самые близкие. Именно на этом и построена суть поиска схожих операций в данном примере.
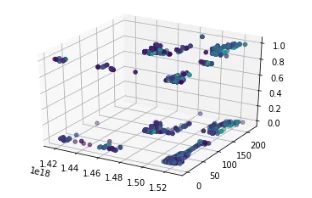
Поступаем с данными ровно так же, как после работы DBSCAN (код выше) и получаем:
X = df[['ORDERDATETIME','SECURCODE','OPERATION']].values
model = KMeans(n_clusters=9900).fit(X)
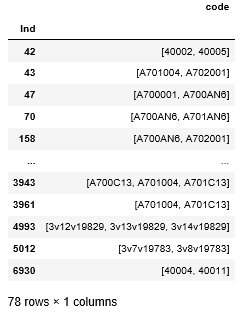
Хотя этот способ понравился нам больше и показался самым правильным и удобным, скорость работы модели очень сильно уменьшается с ростом данных, что не удивительно – размещать большое количество кластеров для модели и проводить огромное количество вычислений становится трудной задачей.
BallTree
Самый простой вариант без применения ML – вычисления расстояний и нахождение ближайших соседей для каждой точки в наборе данных. Тут мы будем искать расстояния всех строк нашего датасета от всех строк нашего датасета. Можем сразу предусмотреть, что минимальное расстояние в таком случае будет между точкой и ее копией, следовательно, будем брать второе минимальное значение.
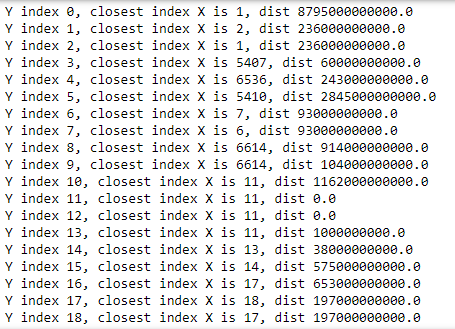
По индексу находим все коды клиента и записываем их в удобном нам виде, выводя при этом вычисленное расстояние:
tree = BallTree(X, leaf_size=2)
dist, ind = tree.query(X, k=2)
l=[]
ll=[]
lll=[]
dist, ind = tree.query(X, k=2)
for i, (ind, d) in enumerate(zip(ind, dist)):
print(f'Y index {i}, closest index X is {ind[1]}, dist {d[1]}')
l.append(ind[0])
ll.append(ind[1])
lll.append(d[1])
for i in range(len(l)):
l[i]=df.iloc[l[i]].CLIENTCODE
ll[i]=df.iloc[ll[i]].CLIENTCODE
l=pd.DataFrame(l)
l.rename(columns={0:'Ind1'}, inplace=True)
l['Ind2']=ll
l['DIST']=lll
l = l.query('DIST>0 & Ind1 != Ind2')
l
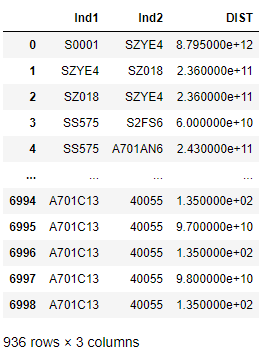
Следует отметить, что с данными, собранными таким образом, работать проще – есть возможность смотреть расстояние, а, следовательно, и значимость сходства.
Исходя из проведённой работы можно сделать вывод, что, несмотря на то, что способы нахождения сходных операций клиентов разные и используют различные математические методы, вывод дают приблизительно похожий. Это значит, что любой из методов можно использовать в работе для сужения границ поиска схожих операций. Остается вопрос выбора более удобного инструмента для конкретной задачи – жертвовать скоростью в угоду удобства или самому искать применения найденным расстояниям. Решать вам!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
