Время прочтения: 3 мин.
Рассмотрим визуализацию результата работы алгоритма Nettack, основанного на инкрементных вычислениях. Для выполнения визуализации необходимо использовать библиотеку matplotlibс использованием пакета pyplot. Matplotlib — библиотека, вдохновлённая эмуляцией команд программного обеспечения Mathworks MATLAB. Важнейшей особенностью этой библиотеки является глобальные стиль, т.е. легкодоступность функций для пользователей на верхнем уровне и отсутствие концепции импорта python. Обозначим импортированный пакет как plt для большей читаемости кода. Благодаря неявному определению в языке Python при выполнении импорта пакета plt, создается полностью готовый экземпляр со всеми графическими возможностями.
from matplotlib import pyplot as pltИспользуя ключевое слово def, создадим функцию do_abscissa_name со списком формальных имён nx и proper. При рассмотрении тела функции do_abscissa_name мы заметим, что при совпадении формальных имён возвращается строка маркирующая значение на оси абсцисс графа.
def do_abscissa_name(nx, proper):
if nx==proper:
return “Class {}\n(proper)”.format(nx)
return “Class {}”.format(nx)
Далее, используя экземпляр класса plt.figure(figsize=(12,4)), создадим область Figure необходимого размера. Следующей строкой с использованием plt.subplot(1, 2, 1) разместим одну строку в двух столбцах на первом графе. После это в цикле происходит описание определение вида данных, отражённых в графе, обозначающих результат выполнения алгоритма Nettack. Мы задаем цвет колонок, размер и расположение на графе. Стоит подробнее сказать об экземпляре класса bar, который строит гистограмму в области Figure. Формальные имена классаplt.bar(x_nxs, block, color=color) задают вид оси абсцисс — x_nxs, оси ординат – block, а также цвет для столбцов гистограммы — color=color.
figure = plt.figure(figsize=(12,4))
plt.subplot(1, 2, 1)
center_nxs_clean = []
for nx, block in enumerate(class_distrs_clean.T):
x_nxs= np.arange(len(block)) + nx*(len(block)+2)
center_nxs_clean.append(np.mean(x_nxs))
color = ‘#555555’
if nx == nettack.label_u:
color = ‘darkgreen’
plt.bar(x_nxs, block, color=color)
Прежде всего выполняем захват текущей оси с помощью класса plt.gca(), после этого необходимо установить диапазон оси, используя класс plt.ylim((-0.05, 1.05)), а также подпишем ось абсцисс для наглядности при помощи класса plt.ylabel(«Predicted probability»). Выполним присвоение меток по заданной оси, используя aks.set_xticks(center_nxs_clean). Назначим метки самой оси для потенциального использования в легенде, прописывая aks.set_xticklabels([do_abscissa_name(k, nettack.label_u) for k in range(_K)]). В завершение создадим заголовок для нашей гистограммы используя экземпляр set_title.
aks=plt.gca()
plt.ylim((-0.05, 1.05))
plt.ylabel(“Predicted probability”)
aks.set_xticks(center_nxs_clean)
aks.set_xticklabels([do_abscissa_name(k, nettack.label_u) for k in range(_K]))
aks.set_title(“Predicted class probabilities for node {} on clean data\n({} re-trainings)”.format(nettack.u, retrain_iters))
Для полного выполнения визуализации пропишем экземпляр класса plt.tight_layout(), который выполнит настройку заголовку для гармоничного вписывания его в полученный граф и необходим экземпляр класса plt.show() для отображения полученного результата.
plt.tight_layout()
plt.show()
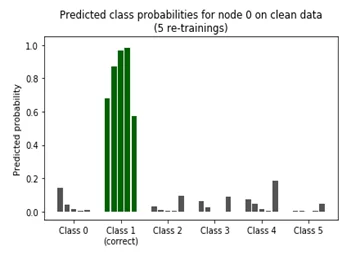
Таким образом, мы получили наглядную гистограмму, иллюстрирующую результат работы алгоритма Nettack. Мы видим, что прогнозируемая вероятность для узла 0 на основе «очищенных» данных после проведения 5 повторных испытаний принимает максимальное значение (стремится к 1) для класса решений 1. Первый класс решений является наиболее вероятным и именно его мы принимаем за правильный.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)