Время прочтения: 5 мин.
Градиентный спуск считается самым предпочтительным способом оптимизации нейронных сетей. Однако обычно его различные вариации используются как черный ящик при обучении нейронной сети, поэтому для исследователя достаточно трудно оценить целесообразность использования того или иного метода при обучении. В данной статье расскажем о том, как работают различные алгоритмы градиентного спуска на Python и что происходит с функцией потерь при обучении нейронной сети.
Семь различных методов будут применены для тестовой функции Himmelblau. Перед нами ставится задача найти такие аргументы, при которых значение функции будет минимально.
Существует несколько тестовых функций для оптимизации, они необходимы для изучения различных ситуаций, с которыми могут сталкиваться алгоритмы оптимизации, в нашем случае – градиентный спуск. Функция Himmelblau является двумерной, то есть на вход она принимает два значения (x, y). Также она имеет 4 глобальных оптимума, то есть мультимодальна. Для нашего исследования будет выбран один из глобальных минимумов. Для того, чтобы найти экстремум, необходимо найти градиент функции. Градиентный спуск – это метод оптимизации первого порядка, то есть необходимо взять первую производную от тестовой функции, чтобы вычислить градиент.
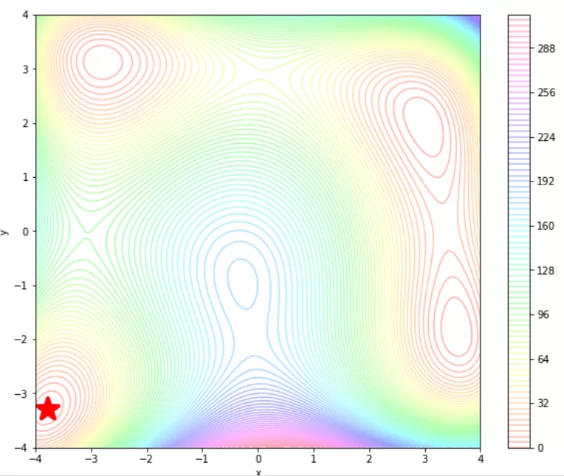
Ниже представлено, как выглядит функция Himmelblau на Python, а также ее производная и начальные параметры. Функция определена на области , но мы взяли кусочек области поменьше. Также задали один глобальный минимум и начальную точку, из которой будем к нему стремиться. На картинке изображены линии уровня функции, звездочкой отмечен глобальный минимум.
def himmelblau(x,y):
return (x**2 + y - 11)**2 + (x + y**2 -7)**2
def himmelblau_grad(x,y):
return np.array([4*x*(x**2 + y -11) + 2*(x + y**2 -7), 2*(x**2 + y - 11) + 4*y*(x + y**2 - 7)])
himmelblau_limits = (-4.0, 4.0)
himmelblau_optim = (-3.779310, -3.283186)
himmelblau_init = (-1.0, -1.0)
Скорость обучения определяет размер шагов, которые используются для достижения минимума. Существует три варианта градиентного спуска, которые отличаются тем, сколько данных мы используем для вычисления градиента целевой функции – batch, stochastic и mini-batch. Однако, при использовании данных вариантов градиентного спуска, возникает ряд проблем. Во-первых, маленькое значение скорости обучения приводит к медленному обучению, а большое значение препятствует нахождению экстремума, и функция потерь может даже расходиться. Во-вторых, главной проблемой оптимизации является то, что есть риск застрять в локальном минимуме или седловой точке, для стохастического градиентного спуска это распространенная проблема. Таким образом, для решения вышеперечисленных проблем существуют следующие алгоритмы:
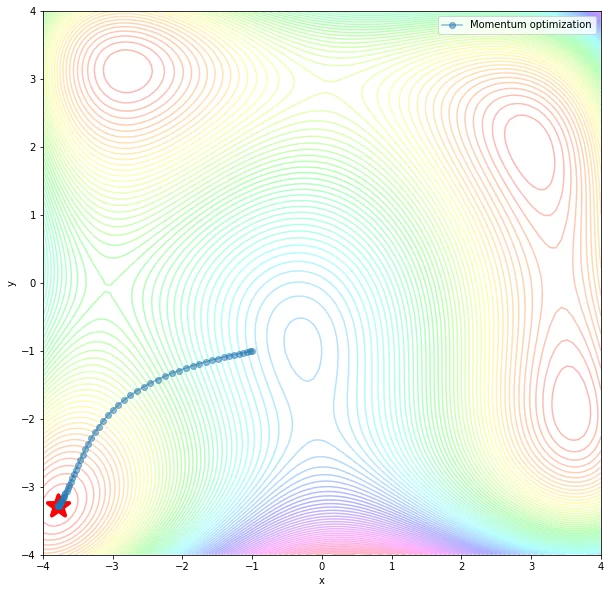
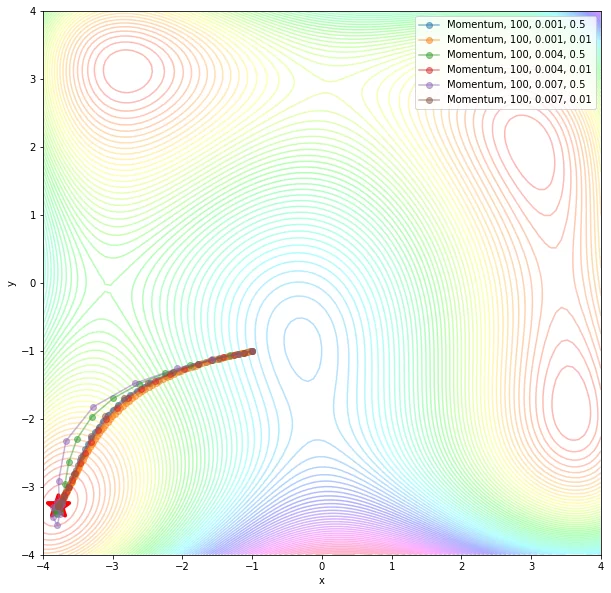
Функция Momentum – ускоряет SGD в нужном направлении и гасит колебания SGD за счет добавления параметра для прошедшего значения шага назад. В коде ниже приведены наилучшие параметры, с помощью которых удалось дойти до глобального минимума. На картинках изображены линии уровня и итерации, за сколько алгоритм добирается до оптимума.
def Momentum(fun, grad_fun, init, n_iterations, eta, b):
traj = [np.array(init)]
v = 0
for k in range(n_iterations):
x = traj[-1]
v = v * b - eta * grad_fun(x[0], x[1])
x = x + v
traj.append(x)
return np.array(traj).T
momentum_traj = Momentum(my_fun, my_grad, my_init,
n_iterations=100, eta=0.001, b = 0.5)
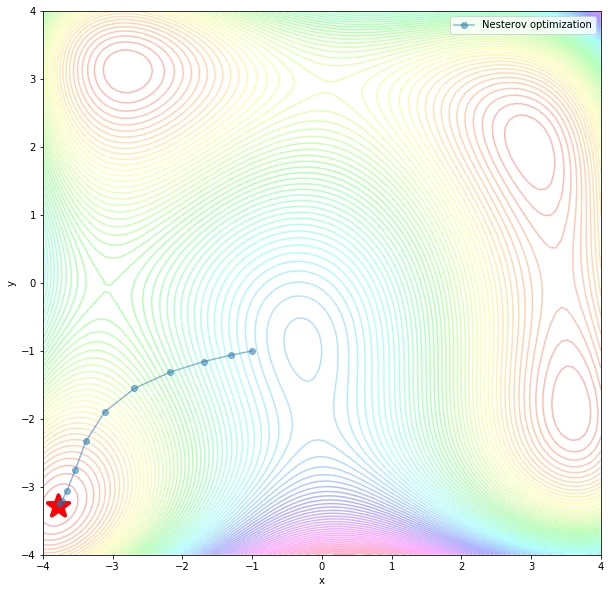
Nesterov momentum – похожий метод на Momentum с небольшим изменением. Также затухает вертикальные колебания.
def Nesterov(fun, grad_fun, init, n_iterations, eta, b):
traj = [np.array(init)]
v = 0
for k in range(n_iterations):
x = traj[-1]
x = x + v * b - eta * grad_fun(x[0] + b * v, x[1] + b * v)
traj.append(x)
return np.array(traj).T
nesterov_traj = Nesterov(my_fun, my_grad, my_init,
n_iterations=10, eta=0.01, b = 0.5)
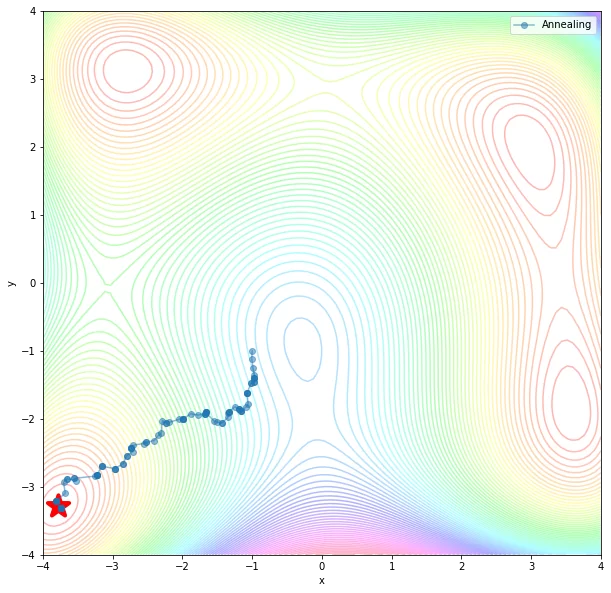
Simulated Annealing – метод отжига. Для его реализации необходимо знать убывающую функцию изменения температуры с течением времени, которая определяет время работы алгоритма, и функцию, которая порождает новое состояние.
def annealing(fun, init, n_iterations, t0 = 1.0, q=0.8, step_size=0.1):
traj = [np.array(init)]
t = t0
for k in range(n_iterations):
x = traj[-1]
proposal = np.random.normal(loc=x, scale=step_size)
log_alpha = (fun(x[0], x[1]) - fun(proposal[0], proposal[1]))/t
if np.log(np.random.random()) < log_alpha:
x = proposal
traj.append(x)
t *= q
return np.array(traj).T
annealing_traj = annealing(my_fun, my_init, n_iterations=100)
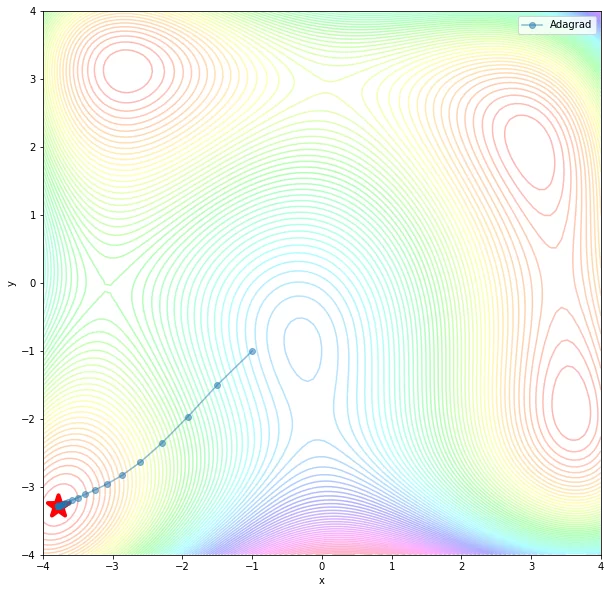
Adagrad – в данном методе скорость обучения для каждого параметра меняется в зависимости от их изменений на предыдущих шагах.
def Adagrad(fun, grad_fun, init, n_iterations, eta, eps=1e-7):
traj = [np.array(init)]
s = 0
for k in range(n_iterations):
x = traj[-1]
grad = grad_fun(x[0], x[1])
s += grad**2
x = x - eta / np.sqrt(s + eps) * grad_fun(x[0], x[1])
traj.append(x)
return np.array(traj).T
adagrad_traj = Adagrad(my_fun, my_grad, my_init,
n_iterations=100, eta=0.5)

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
