Время прочтения: 7 мин.
Всем привет!
В публикации хочу рассказать простым языком, как математика, вероятности и распределения помогают анализировать клиентов и эффективно использовать внутренние ресурсы компании.
Ни для кого не секрет, что многие передовые компании, чья деятельность направлена на обслуживание клиентов, стремятся поддерживать высокий уровень услуг и клиентской поддержки. Вполне логичное предположение, что увеличение количества клиентов является одним из показателей успешности компании.
Однако постоянное увеличение потока клиентов, в особенности изменение активности клиентов в зависимости от времени, может вызывать сложности в организации работы клиентской поддержки.
Рассматриваемый кейс продемонстрирует подход к решению данных вопросов и является одной из задач теории массового обслуживания, где неотъемлемую роль играет математика. Одно из теоретических решений кроется в использовании экспоненциального распределения.
Изначально необходимо обратиться к теории вероятности, где дается определение случайной величины (далее – СВ). Данным термином называют численное выражение итогов случайного феномена или эксперимента. Примерами может служить длительность безотказной работы банкомата и время ожидания ответа оператора при обращении клиента в колл-центр.
Как я выяснила, случайная величина может принимать различные числовые значения. Тогда для каждого исхода события (конкретного значения) можно посчитать вероятность его наступления.
Ключевой характеристикой СВ является её функция распределения F(x). Проще говоря, это функция, значение которой в любой точке x равняется вероятности того, что СВ примет значение меньше, чем x.
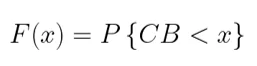
Если данная функция является непрерывно дифференцируемой, т.е. от нее можно взять производную, то СВ называется непрерывной.
Визуально оценивая, функция должна быть непрерывной и не иметь острых углов.
Производная от функции распределения называется плотностью вероятности или кривой ее распределения.
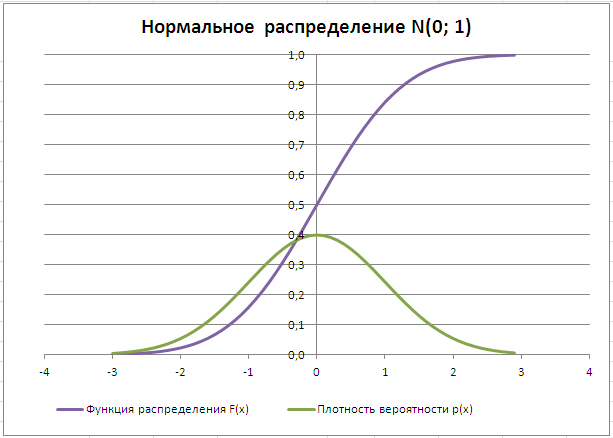
Существует несколько распределений, активно используемых для решения практических задач. Одним из таких является экспоненциальное (где альфа (α) – параметр), которое буду использовать в дальнейшем. Его функция распределения и плотность, соответственно, принимают вид:
- функция распределения:
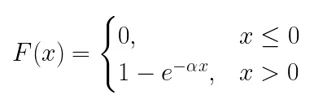
- плотность вероятности:
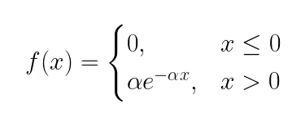
Параметр α является обратно пропорциональным математическое ожиданию и характеризует СВ.
Представлю упрощенную ситуацию в колл-центре, где для каждого оператора формируется независимый поток звонков. То есть если в колл-центре 20 операторов, то каждый двадцатый звонок приходит определенному сотруднику (отсутствует перераспределение звонков в зависимости от загруженности). Рассмотрю кейс для одного оператора.
Исходя из базы данных колл-центра можно посчитать медианное время (серединное значение) между последовательными звонками клиентов.
Время между последовательными звонками клиентов в тех поддержку является случайной величиной, распределенной по экспоненциальному закону.
Для нахождения медианного значения беру датасет для одного оператора, фиксирующего время начала и конца каждого разговора. В дополнительную колонку записываю дельты (разность между концом диалога и началом следующего). Далее по этому столбцу ищу медианное значение m. В моём случае оно составляет 90 секунд (1,5 мин).
Это значение связано с параметром α по следующей формуле:
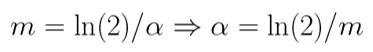
Подставив значения получаю:
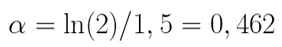
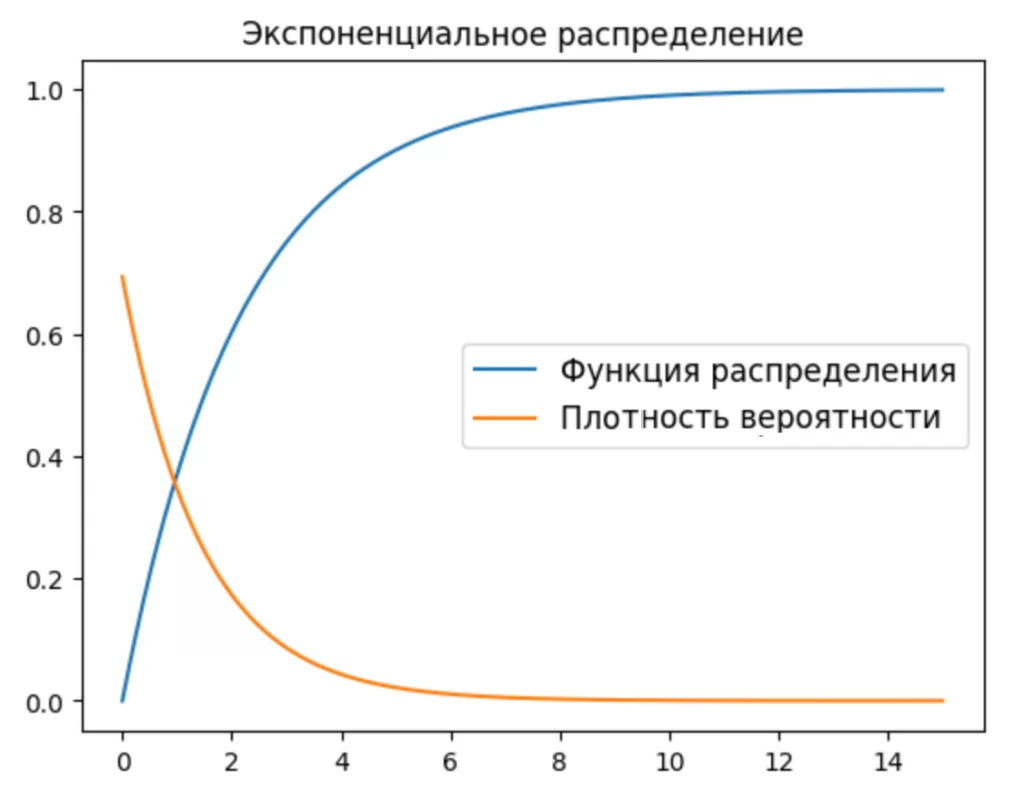
Напишу функцию распределения для моего конкретного случая и построю её график.
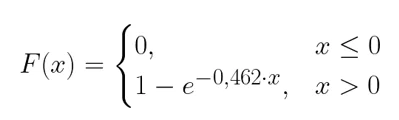
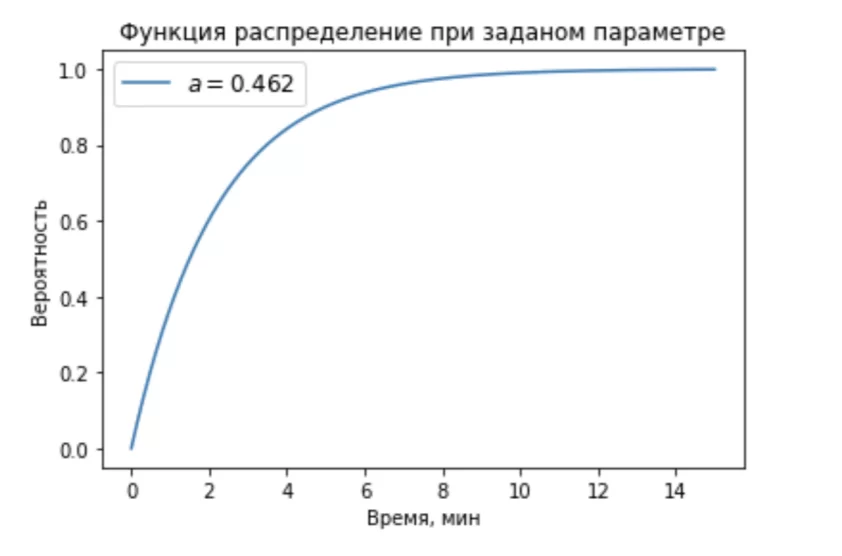
Какие выводы можно сделать из данного распределения?
Найду вероятность, что новый клиент позвонит в течение 2 минут после предыдущего разговора. Иными словами, найду вероятность события:
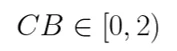
Для этого воспользуюсь формулой для функции распределения и получу:
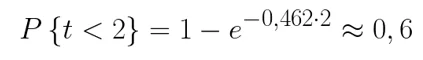
Интерпретируя результат, можно сказать, что вероятность обращения клиента не позднее, чем через 2 минуты после предыдущего больше 60%.
Другими словами, вероятность, что оператор будет сидеть без дела 2 минуты равна 40%.
Такой анализ помогает находить баланс между необходимостью компании всегда находиться “на связи” и эффективным использованием ресурсов, таких как материальные средства и рабочая сила.
Сейчас рассмотрю, что будет меняться при изменении интенсивности потока звонков клиентов. Допустим, компания увеличивает количество клиентов и не меняет число операторов. Тогда временные промежутки между звонками клиентов уменьшатся, а, следовательно, уменьшится и медианное значение.
Для сравнения проанализирую ситуации, когда медиана уменьшается до 1 мин и увеличивается до 2 мин.
Посчитаю коэффициенты α и построю графики распределения для различных значений интенсивности.
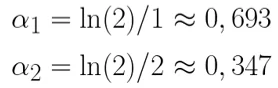
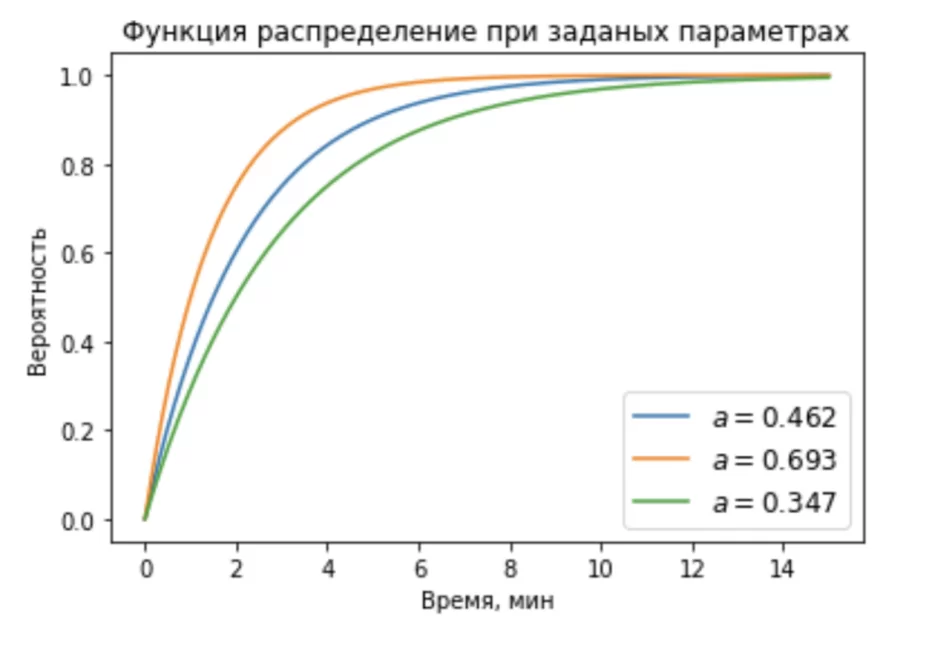
Таким образом, при увеличении интенсивности потока звонков вероятность, что оператор получит входящий звонок в течение 2 мин с окончания предыдущего, увеличивается.
Найду эту вероятность для сравнения:
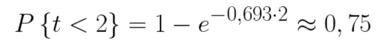
Увеличение потока звонков в 1.5 раза приводит к увеличению вероятности загрузки сотрудника в течение 2 минут на 15%.
На практике необходимо учитывать больше факторов. Поэтому необходима более гибкая функция, содержащая больше параметров.
В данной задаче такой функцией является Гамма-распределение, имеющее плотность распределения:
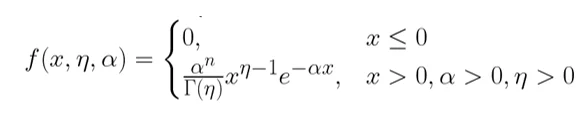
Где гамма-функция определяется следующим образом:
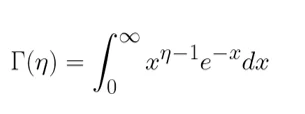
И для положительных целых η (“эта”) рассчитывается как:
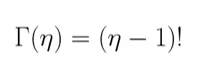
Экспоненциальное распределение является его частным случаем при η=1.
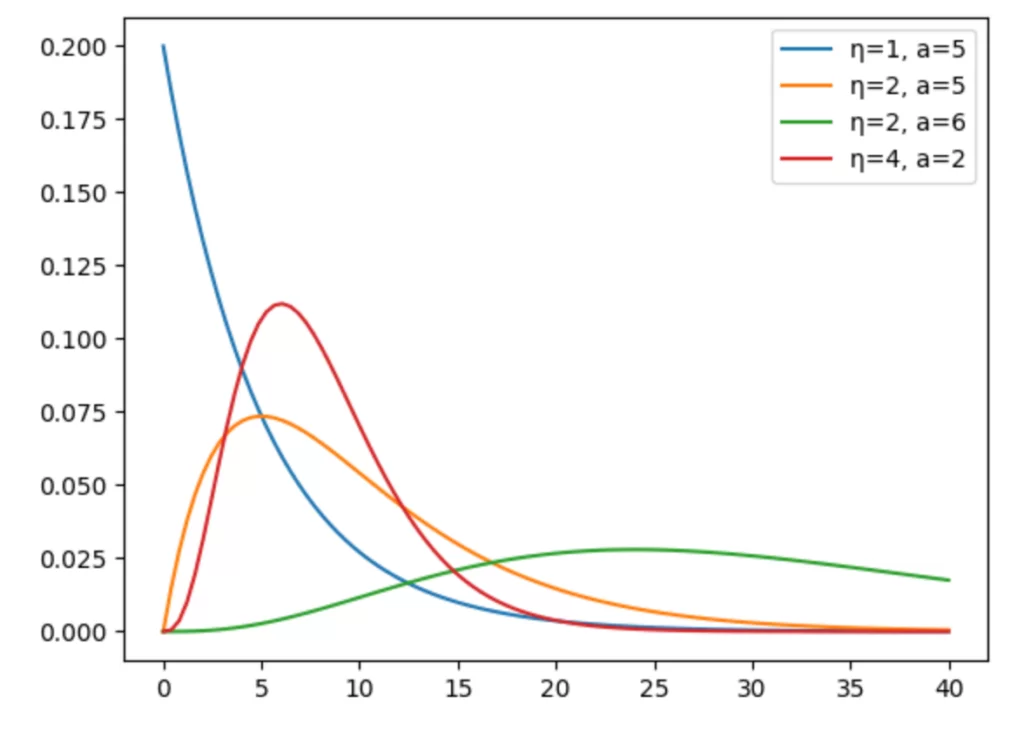
Параметр η описывает форму кривой. При η <=1 она является монотонно убывающей, при η>1 функция имеет пик в точке (η-1)/α. Параметр α отвечает за масштаб.
Применю это распределение к своей задаче.
С помощью Гамма-распределения можно описать время, за которое произойдет η независимых событий, интенсивность которых равна α.
Пусть условия задачи аналогичны, однако, согласно нормативам работы оператора, в колл-центре считается количество принятых звонков за смену. В среднем оператор принимает около 120 – 140 звонков.
Получается, есть норма количества звонков для одного оператора. Возьму η~130. Как было рассчитано ранее, интенсивность α=0,462. Тогда промежуток времени, за который оператор ответит на 130 звонков, будет случайной величиной.
Так как стандартный рабочий день длится 8 часов, то можно найти вероятность, что оператор будет эффективно отрабатывать и отвечать на 130 обращений при нашей интенсивности обращений.
Для того чтобы найти вероятность попадания случайной величины в промежуток 0 – 8 часов, необходимо взять интеграл от плотности вероятности на данном промежутке (0 ч.; 8 ч.).
Возьмем интеграл от Гамма-функции с помощью библиотеки scipy для языка Python и получу искомое значение:
import scipy.stats as stats
from scipy import integrate
def f(x):
return stats.gamma.pdf( x, a=0.462, scale = 190 )
v, err = integrate.quad(f, 0, 8*60)
print(v)
Вывод:
0.9782768492136601
Видно, что вероятность практически равна 1. Таким образом, можно варьировать количество звонков и оценивать вероятность.
Благодаря таким наблюдениям и расчетам можно оценивать эффективность сотрудников и устанавливать индивидуальные нормы в компании, удовлетворяющие специфике работы.
Данный пост не предполагает демонстрацию реализации программы для конкретного датасета и параметров. Цель — познакомить вас с математическими подходами, которые можно использовать при оценке нагрузки и эффективности.
А как еще можно регулировать данную ситуацию? Сколько сотрудников нанимать при увеличении клиентской базы?
На эти и многие аналогичные вопросы, возникающие в процессе регулирования потока клиентов, дает ответы исследование этой волшебной функции экспоненциального распределения и многих других.
Спасибо за внимание!

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
