Время прочтения: 6 мин.
Обработка изображений с помощью нейросетей широко используется в настоящее время. Это полезно, например для классификации изображений. Одним из известных примеров такой задачи является классификация животных на изображении. Нейросеть, обучаясь на предоставленном ей наборе данных, разделяет изображения по категориям и способна отличать кошку от собаки с определенной точностью. Или, например, не менее популярная задача классификации чисел, где нейросеть учится визуально отличать числа от 0 до 9. Задачи имеют широкое применение: в распознавании рукописного текста, анализе объектов на изображении, описании объектов, распознавании образов, определении опасных заболеваний на медицинских снимках и многие другие.
Наиболее эффективно с такой обработкой справляются сверточные нейронные сети (convolutional neural networks, сокращенно – CNN). В предыдущей статье мы рассматривали особенности сверточной нейронной сети и самой операции свертки. В данной статье мы решим задачу распознавания стегосообщения в контейнере изображения и научимся пректировать архитектуру нейронной сети с помощью фреймворка pyTorch. Поставленная цель является достаточно сложно реализуемой ввиду того, что визуальные искажения на зашифрованных изображениях практически незаметны. Для решения мы будем использовать предварительно обработанные изображения с помощью высокочастотных Вейвлет-ориентированных фильтров Добеши. Ниже представлен пример подобного распознавания с примененным фильтром предварительной обработки изображения. Слева пустой контейнер, справа – заполненный.

Давайте рассмотрим пример архитектуры нейронной сети для решения поставленной задачи. Это задача классификации изображений по двум классам. Размер входных изображений будет 256х256 пикселей, один цветовой канал. Будем использовать глубокую нейронную сеть с пятью слоями, вы можете настраивать и кастомизировать слои по своему усмотрению.
Архитектура сверточной нейронной сети состоит из последовательно идущих операций свертки и операций пакетной нормализации, пулинга по среднему/максимальному значению, dropout и других. Их можно включать и исключать из получившейся модели нейронной сети. Архитектура нейронной сети для решения конкретной задачи представлена на рисунке 1.
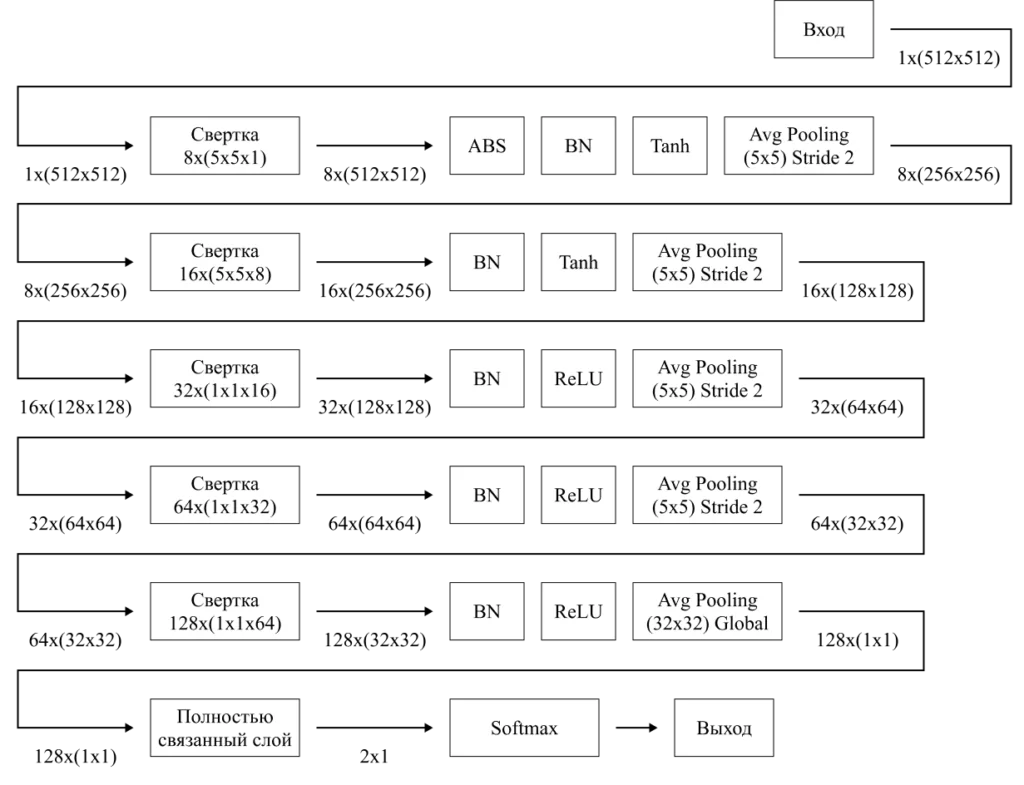
Объясним, что тут происходит: ядро свертки размерностью 5х5 пикселей проходится по изображению, в результате чего выявляются признаки, shape изображения меняется и оно приобретает новую размерность. На первых двух сверточных слоях мы используем функцию активации Tanh, после – ReLU.
Помимо представленных функций активации, существует достаточно много других функций активации, при этом общий смысл их использования сводится к тому, чтобы определить выходное значение нейрона пользуясь пороговым значением и взвешенной суммой входов. То есть, функция активации задает правило, по которому будет осуществляться выбор того или иного решения. Функции активации могут быть линейными и нелинейными. К линейным относится ступенчатая функция активации, линейная функция активации. К нелинейным относятся такие функции как, например, сигмоида, гиперболиче- ский тангенс, ReLU, Leaky ReLU, Tanh, Gaussian и многие другие. Обычно я использую ReLU или Tanh как самые универсальные функции активации.
Переобучением называется ситуация, когда алгоритм сильно лучше классифицирует обучающую выборку, чем тестовую. Dropout необходим для того, чтобы предотвратить процесс переобучения нейронной сети. Он выключает нейроны с определенным процентом вероятности и таким образом помогает сети не «заучивать» правильные ответы, а находить закономерности. Пакетная нормализация, в свою очередь, позволяет повысить производительность и стабильность нейронной сети, также помогает противодействовать переобучению.
Пулинг по среднему значению помогает вернуть среднее значение из части изображения, при этом размерность изображения уменьшается в два раза, но извлекаются признаки. Существуют также другие виды пулинга, например пулинг по максимальному значению. Не сложно понять, что он позволяет вернуть максимальное значение выбранной части изображения.
Последним этапом работы нашей нейронной сети является прохождение через полностью связанный слой, который позволяет выделить доминирующие признаки из уже преобразованного в вектор изображения с помощью техники Softmax. Таким образом, это заключительный этап анализа изображения, здесь мы можем задать количество классов, которое будет равно количеству выходных значений.
Все эти этапы можно контролировать с помощью инструмента pyTorch.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 8, kernel_size=5, stride=1, padding=2, bias=False)
self.bn1 = nn.BatchNorm2d(8)
self.conv2 = nn.Conv2d(8, 16, kernel_size=5, stride=1, padding=2, bias=False)
self.bn2 = nn.BatchNorm2d(16)
self.conv3 = nn.Conv2d(16, 32, kernel_size=1, stride=1, padding=0, bias=False)
self.bn3 = nn.BatchNorm2d(32)
self.conv4 = nn.Conv2d(32, 64, kernel_size=1, stride=1, padding=0, bias=False)
self.bn4 = nn.BatchNorm2d(64)
self.conv5 = nn.Conv2d(64, 128, kernel_size=1, stride=1, padding=0, bias=False)
self.bn5 = nn.BatchNorm2d(128)
self.fc = nn.Linear(128*1*1, 2)
def forward(self, x):
out = F.tanh(self.bn1(torch.abs(self.conv1(kernel))))
out = F.avg_pool2d(out, kernel_size=5, stride=2, padding=2)
out = F.tanh(self.bn2(self.conv2(out)))
out = F.avg_pool2d(out, kernel_size=5, stride=2, padding=2)
out = F.relu(self.bn3(self.conv3(out)))
out = F.avg_pool2d(out, kernel_size=5, stride=2, padding=2)
out = F.relu(self.bn4(self.conv4(out)))
out = F.avg_pool2d(out, kernel_size=5, stride=2, padding=2)
out = F.relu(self.bn5(self.conv5(out)))
out = F.adaptive_avg_pool2d(out,(1,1))
out = out.view(out.size(0), -1)
out = self.fc(out)
return out
net = Net()
Здесь представлена архитектура сети, состоящая из пяти слоев свертки, на каждом слое задаются индивидуальные параметры нейронной сети такие как размер ядра свертки, bias, padding и stride. Также здесь указываются применяющиеся функции активации.
Процесс обучения нейронной сети состоит из:
- формирования выходных значений за счет прямого распространения ошибки (scores);
- подсчета loss между тем что выдает модель и целевыми значениями;
- обнуления градиентов;
- обновления градиентов за счет обратного распространения ошибки;
- оптимизации.
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, betas=(0.9, 0.99))
for i in range(epochs):
logits = model(x_batch) # вычисляем scores
loss = criterion(logits, y_batch) # вычисляем loss
history.append(loss.item()) # записываем в историю обучения
optimizer.zero_grad() # зануляем градиенты
loss.backward() # вычисляем градиент
optimizer.step() # оптимизатор
Таким образом мы решили задачу распознавания стегосообщения с помощью классификации изображений по двум классам – есть стегосообщение и стегосообщение отсутствует. Получаем следующие выходные данные по точности распознавания полученной модели. Результат достаточно высокий – 91%, но стоит заметить, что достигнут он в основном благодаря предварительной обработке входных данных.

Как видите, проектировать нейронные сети не так сложно, как может показаться. Единственным ограничением, по моему скромному мнению, являются аппаратные возможности вашего устройства и ограниченная выборка данных для проведения обучения в связи со сложностью их получения и проставления меток классов вручную перед обучением. Надеюсь, сложности вас не остановят в погружении в этот замечательный мир глубокого обучения. Желаю удачи и не останавливаться на достигнутом!

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
