Время прочтения: 6 мин.
В этой статье я бы хотела рассмотреть несколько линейных моделей регрессии, охватывая некоторые базовые подходы, которые лежат в основе математики.
Данная статья направлена на разработку оптимальной линейной модели, которая применима конкретно к рассматриваемому проекту.
Вне зависимости от уровня Ваших знаний, статья подкреплена примерами для формирования подходов к предмету, поэтому, сложности в понимании реализации кода на Python у пользователя возникнуть не должно.
Давайте перейдем к теории и к примерам «на пальцах»:
Линейная модель – это модель, которая чаще других используется на практике. Помимо того что модель используется для регрессии, ее также можно использовать и для классификации объектов. Для большего понимания, линейные модели предсказывают выходы на основании заданной функции, которая соответствует нашей модели.
Давайте рассмотрим пример, который используется в теории математики 7-8 классов:
Найдите связь между следующими пунктами: (1,4), (2,7), (3,10), (4,13), (5,16).
В качестве входных параметров являются значения x(1,2,3,4,5), которые образуют значения выходов, соответственно, x(4,7,10,13,16). Не трудно понять, что зависимостью между входом и выходом является функция прямой с наклоном 3, при которой заданный вход значения x даёт нам на выходе значение y: y = 3*x+1.
Таким образом, свойство линейных моделей – это спрогнозировать будущие значения выходных данных на соответствующих входных значениях. Например, мы понимаем, что значения выхода (y) = 22 для вышеупомянутой функции прямой предсказано по значению входа (x) = 7.
Теперь давайте смоделируем и обобщим систему, которая будет описывать нашу модель:
y = b + w[0]*x[0]+ w[1]*x[1]+ w[2]*x[2]+…+ w[n]*x[n], где
y – прогнозируемое значение выхода,
x[i] – i значение признака,
w[i] – I значение веса признака,
n – количество значений функций,
b – смещение функции.
Давайте посмотрим линейную регрессию для случайного набора данных на примере реализации небольшого кода с использованием библиотеки Python – sklearn.
Для начала импортируем несколько библиотек: numpy для задания случайного набора данных, matplotlib для отрисовки функции модели и sklearn для прогнозирования и оценки модели.
import numpy as np
import matplotlib.pyplot as pit
from sklearn.linear_model import LinearRegression
В качестве x возьмем значения массива случайных чисел от 1 до 50.
х = np.random.rand(50, 1)Функция представляет следующее задание y:
у = 50 + 10 * x + np.random.randn(50, 1)l_r = LinearRegression()
l_r.fit(x,y)
Метод fit модели пытается найти коэффициенты, которые минимизируют различие между предсказанием по модели данных x_train и реальным значением y_train.
y_pred=l_r.predict(x)
MSE=np.square(np.subtract(y_pred,y)).mean()
Среднеквадратичная ошибка(MSE) – это квадрат расстояния, для которого расстояние для верхней стороны линии оценивается как положительное, а нижняя – отрицательное. Цель состоит в том, чтобы минимизировать ошибку (MSE).
print("MSE_: ",MSE)
print("bias : ", l_r.intercept-)
print("weight :",l_r.coef_)
plt.scatter(x,y)
plt.plot(x,y_pred,color='red')
plt.xlabel('Входные значения')
plt.ylabel('Выходные значения')
plt.show
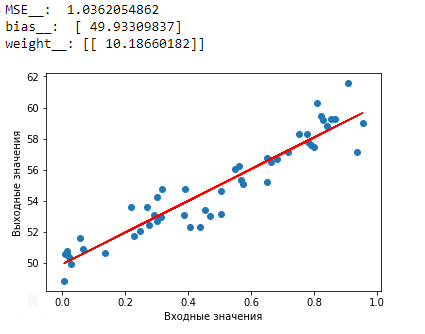
Из примера выше можно увидеть, что линейная регрессия импортируется с библиотекой sklearn, минимизируем MSE с помощью оптимизации сингулярной декомпозиции(SVD), в основе SVD заложены огромные алгебраические уравнения, скрытые от пользователя.
Давайте рассмотрим другие алгоритмы оптимизации решения этой проблемы.
Градиентный спуск является еще одной математической операцией минимизации функции затрат. Идея заключается в том, чтобы минимизировать функцию затрат путем итеративного обновления параметров. Значение веса инициализируется случайно и постепенно сходится к минимуму по скорости обучения.
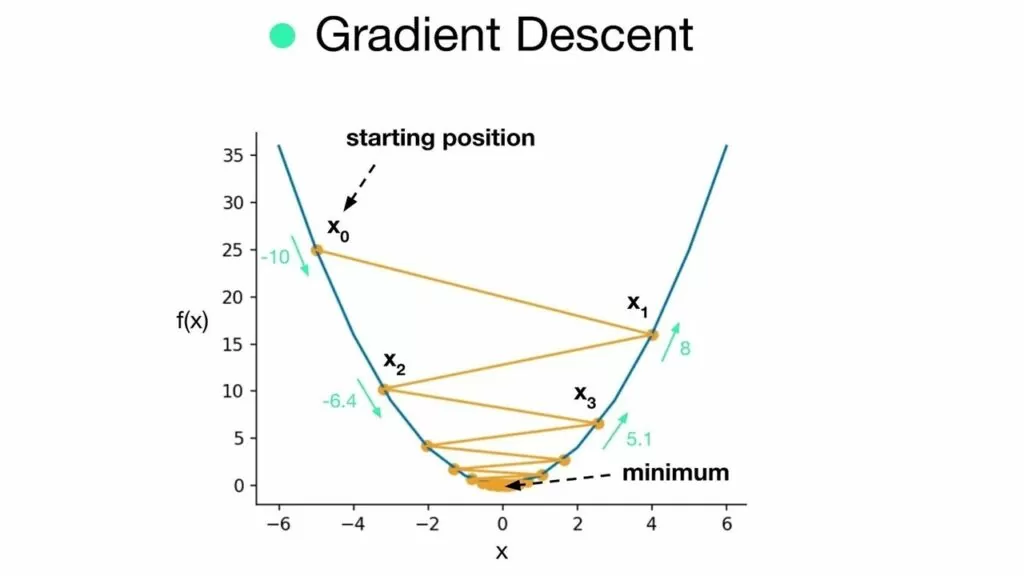
На рисунке выше представлен градиентный спуск с высокой скоростью обучения.
import time
def timeit(method):
def timed(*args, **kw):
ts = time.time()
result = method(*args, **kw)
te = time.time()
if 'log_time' in kw:
name = kw.get(' log_name’, method. name .upperQ)
kw[’log_time'][name] = int((te - ts) * 1000)
else:
print('%r %2.2f ms' % \
(method. name , (te - ts) * 1000))
return result
return timed
def cal_cost(theta,x,y):
m = len(y)
predd = x.dot(theta)
cost = (1/m) * np.sum(np.square(predd-y)) return cost
@timeit
def gradient_descent(x, y, theta, eta=0.01, iterations=1000): data_len = len(y)
for it in range(iterations):
xtheta = np.dot(x, theta)
theta = theta - (1 / data_len) * eta * (x.T.dot((xtheta - y)))
cost = cal_cost(theta, x, y)
return print'"bias :", theta[0],"\nweight :", theta[l],"\ncost : ",cost
lr = 0.3
n_iter = 3000
theta = np.random.randn(2, 1)
x_b = np.c_[np.ones((len(x), 1)), x]
gradient_descent(x_b, y, theta, lr, n_iter)
На выходе получим следующие значения:
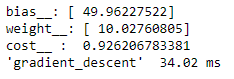
При скорости обучения равной 0,3 и 3000 операций процесс занимает 34.02 мс.
Теперь рассмотрим разницу времени при стохастическом градиентном спуске.
Градиентный спуск вычисляет функцию затрат для каждого значения веса отдельно по всему набору данных с применением частной производной, в то время как стохастический градиентный спуск выбирает случайный экземпляр из набора данных на каждом шаге и вычисляет градиент. Работа только с экземпляром, а не со всем набором данных является более эффективной по скорости выполнения.
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error
@timeiitt
def StochasticRegressor(x,y, penalty='eleasticnet’,
learning_rate='constant',eta0=0.3,max_iter=3000)
sgdr = SGDRegressor(penalty=’elasticnet',learning_rate='constant', eta0=0.3,max_iter=3000)
sgdr.fit(x, y)
ypred = sgdr.predict(x)
mse = mean_squared_error(y, ypred)
return print("bias : ",sgdr.intercept-,"\nweight: "
,sgdr.coef_, "\nMSE : ", mse)
StochasticRegressor(x,y,eta0=0.3)
Как мы видим, при скорости обучения = 0.3 и количеству итераций = 3000 процесс обучения занимает всего 1,3 мс.
Рассмотрим еще два типа моделей, которые можно применить в своем проекте:
Регуляризация L2 – это тип линейной регрессии, который позволяет регуляризовать модель, основан на выборе как можно меньших значений веса. Другими словами, регуляризация ограничивает модель, уменьшая влияние входов на выход, тем самым модель становится регуляризованной и избегает переоснащения этими ограничениями.
Регуляризация L1 – оператор наименьшей абсолютной усадки и выбора (ЛАССО), при этом методе веса некоторых значений принимаются равными нулю, предполагая, что они не влияют на результат.

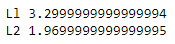
Рассматривая, какое из решений является более эффективным, можно сказать, что функция потерь L2 выводима во всех значениях, в то время, как L1 невыводима в нуле.
При незначительном изменении набора данных L1 изменится больше, чем L2 и решение становится нестабильным.
Успехов в кодировании! 😊

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)