Время прочтения: 7 мин.
При постоянной работе с данными, поступающими из разных источников, часто возникает потребность в поиске «расстояния» между некоторыми текстовыми данными, объединенными некоторыми общими признаками. Ранее мы уже рассматривали ряд метрик, помогающих решать подобные задачи (расстояние Левенштейна — ссылка, Расстояние Хэмминга — ссылка). Сегодня поговорим о, вероятно, лучшей из них(в рамках наших потребностей.
Честно говоря, называть расстояние Джаро — Винклера метрикой расстояния в математическом смысле не совсем верно, т.к. не выполняется следующая аксиома: «расстояние равно нулю тогда и только тогда, когда строки полностью совпадают». В данном случае когда результат 1 – достигнуто «идеальное совпадение», поэтому используется так называемое «сходство Джаро-Винклера», которое получается вычитанием расстояния из единицы. Стоит отметить, что алгоритм построен на вычислении другой метрики – расстояния Джаро, которая предполагает следующее:

Несложно заметить, что в данном случае уже учитывается операция транспозиции. Каждый символ первой строки сравнивается со всеми соответствующими ему символами во второй строке. Количество совпадающих (но отличающихся порядковыми номерами) символов, которое делится на 2, определяет число транспозиций.
В алгоритме, предложенном Винклером, используется коэффициент масштабирования p, что дает более благоприятные рейтинги строкам, которые совпадают друг с другом от начала до определённой длины l, которая называется префиксом. Формула приобретает следующий вид:

Стоит также отметить, что в работах Винклера указана еще одна особенность вычисления данного расстояния. Так называемый «префиксный бонус»(то, что в формуле выделено скобками) прибавляется только в случае если расстояние Джаро «перешагивает» через некоторый «коэффициент усиления», который в свою очередь Винклер указывал равным 0.7.Реализация данного алгоритма ощутимо сложнее, чем реализация расстояния Хэмминга или расстояний Левенштейна/Дамерау-Левенштейна(спасибо Ronnie Overby, за прекрасную реализацию).
Для начала сразу определим обозначенные выше ограничения:
private const double tresholdgain = 0.7;
private const int numfirstchars = 4;
Основные вычисления будут представлять из себя следующее:
public static double Prox(string firstWord, string secondWord, IEqualityComparer<char> comparer = null)
{
comparer = comparer ?? EqualityComparer<char>.Default;
var lLen1 = firstWord.Length;
var lLen2 = secondWord.Length;
//if (lLen1 == 0)
// return lLen2 == 0 ? 1.0 : 0.0;
var SearchRange = Math.Max(0, Math.Max(lLen1, lLen2) / 2 - 1);
var Match1 = new bool[lLen1];
var Match2 = new bool[lLen2];
var NumComm = 0;
for (var i = 0; i < lLen1; ++i)
{
var Startval = Math.Max(0, i - SearchRange);
var Endval = Math.Min(i + SearchRange + 1, lLen2);
for (var j = Startval; j < Endval; ++j)
{
if (Match2[j]) continue;
if (!comparer.Equals(firstWord[i], secondWord[j]))
continue;
Match1[i] = true;
Match2[j] = true;
++NumComm;
break;
}
}
if (NumComm == 0) return 0.0;
var NumTransphalf = 0;
var k = 0;
for (var i = 0; i < lLen1; ++i)
{
if (!Match1[i]) continue;
while (!Match2[k]) ++k;
if (!comparer.Equals(firstWord[i], secondWord[k]))
++NumTransphalf;
++k;
}
var lNumTransposed = NumTransphalf / 2;
double NumCommonD = NumComm;
var Weightval = (NumCommonD / lLen1
+ NumCommonD / lLen2
+ (NumComm - lNumTransposed) / NumCommonD) / 3.0;
if (Weightval <= tresholdgain) return Weightval;
var Maxval = Math.Min(numfirstchars, Math.Min(firstWord.Length, secondWord.Length));
var Posval = 0;
while (Posval < Maxval && comparer.Equals(firstWord[Posval], secondWord[Posval]))
++Posval;
if (Posval == 0) return Weightval;
return Weightval + 0.1 * Posval * (1.0 - Weightval);
}
И в конце делаем следующее:
public static double JaroWinklerDistance(string firstWord, string secondWord, IEqualityComparer<char> comparer = null)
{
return 1.0 - Prox(firstWord, secondWord, comparer);
}
Сам Винклер использовал свой код, реализованный на C, в таблице опечаток, а также позднее для длинных строк.
1.В первом кейсе рассмотрим разные случаи перестановки символов
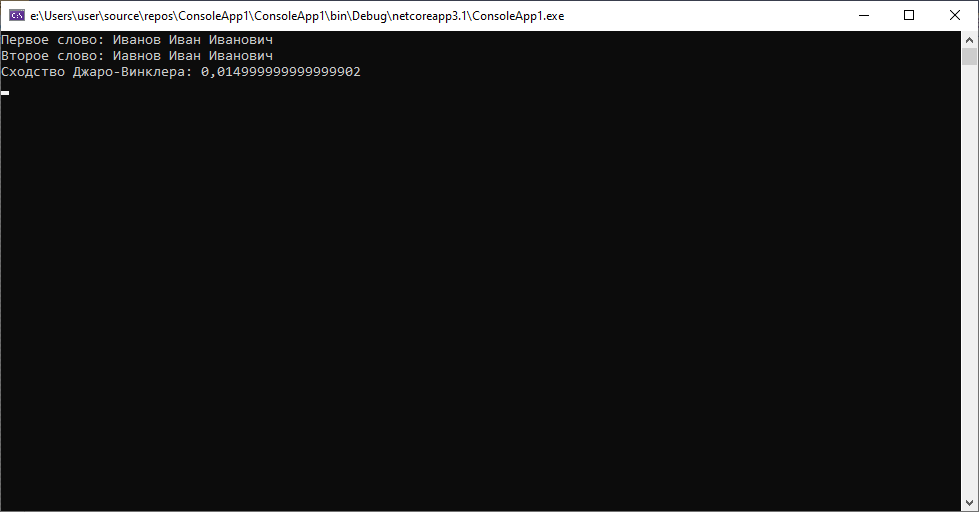
Мы видим опечатку в фамилии во втором случае. Расстояние маленькое, как и ожидалось, ведь алгоритм предполагает учет перестановок. Слегка усложним задачу и допустим еще пару «изолированных» перестановок символов в примере, чтобы добиться другого результата.
Дистанция, как мы видим, ощутимо «подросла до 0.045. Следующая ситуация, когда будут переставлены два символа, не являющиеся соседними.
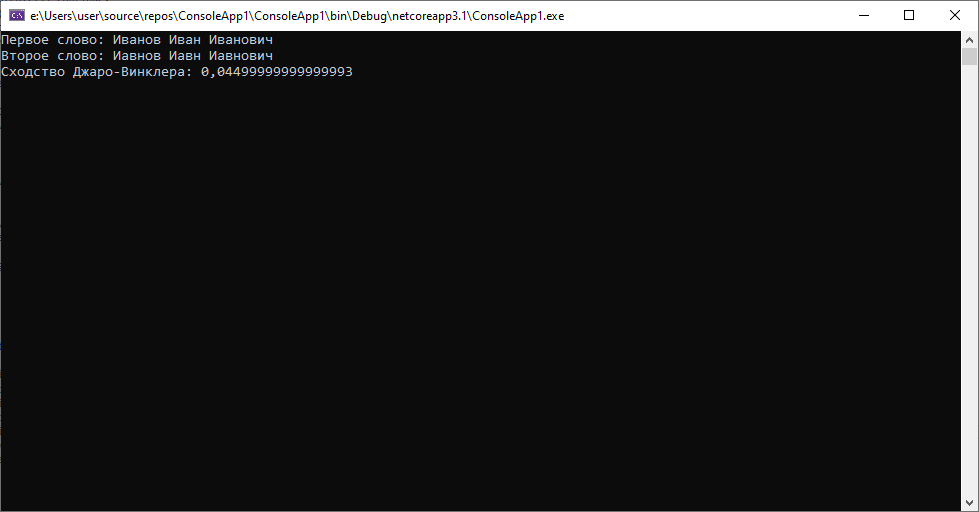
Алгоритм снова без проблем показывает достаточно маленький результат в 0.01(3). Это хорошо.
2. Второй кейс будет рассматривать ситуации, когда в строке имеется явные ошибки, связанные с набором символов, отсутствующих в наборе, пропуск символов. Для начала пропуски.
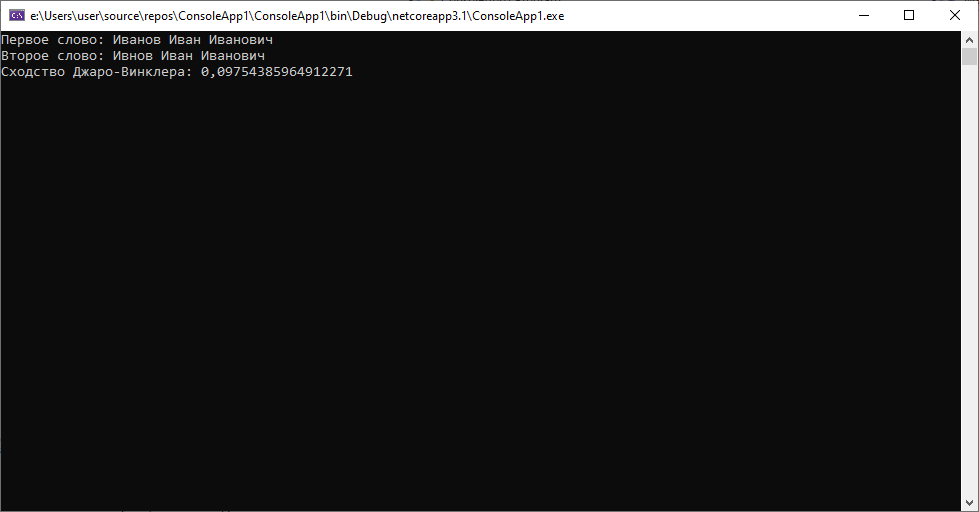
Результат почти 0.1, это больше, чем в любом из предыдущих случаев, но при этом все еще достаточно мал, чтобы позволять нам, не глядя на данные утверждать, что это один и тот же человек. Теперь попробуем несколько пропусков.
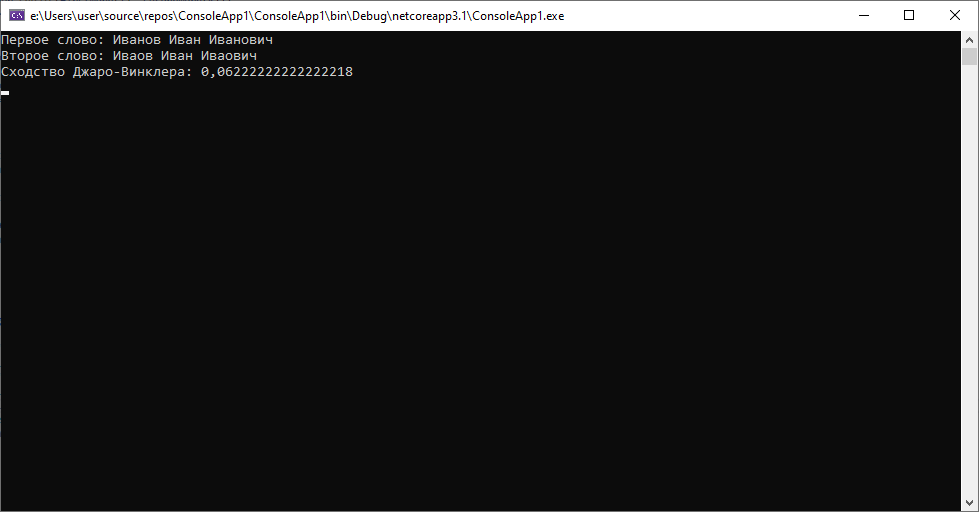
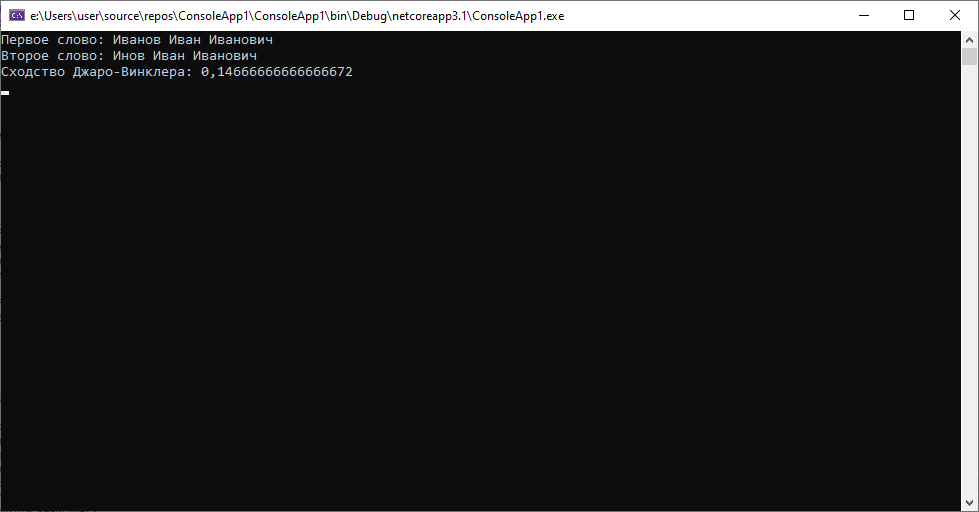
И в случае пропуска символов в разных местах и при пропуске двух символов подряд алгоритм справился хорошо. Попробуем замену символов.
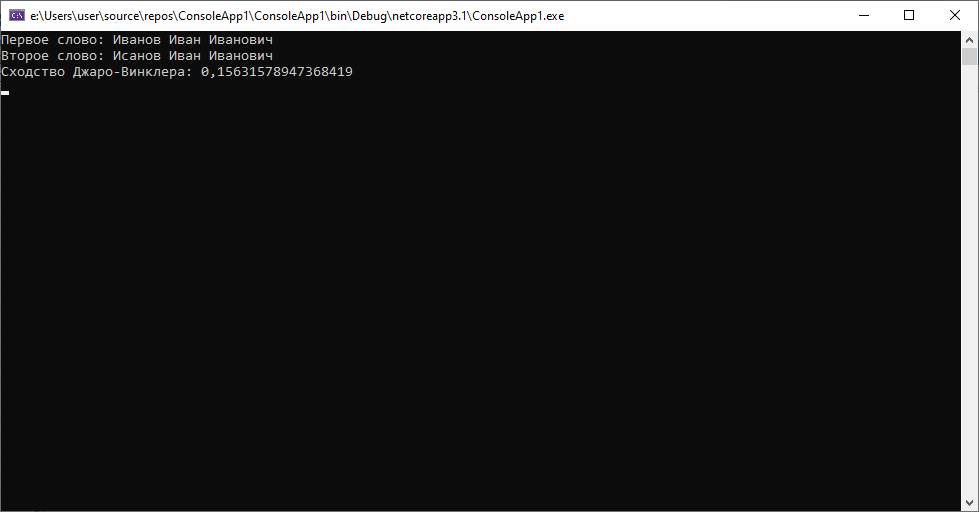
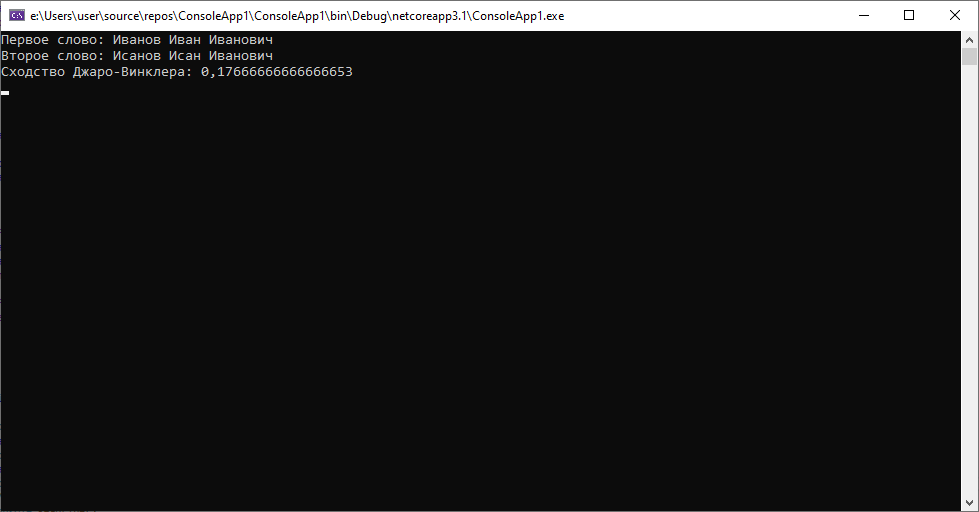
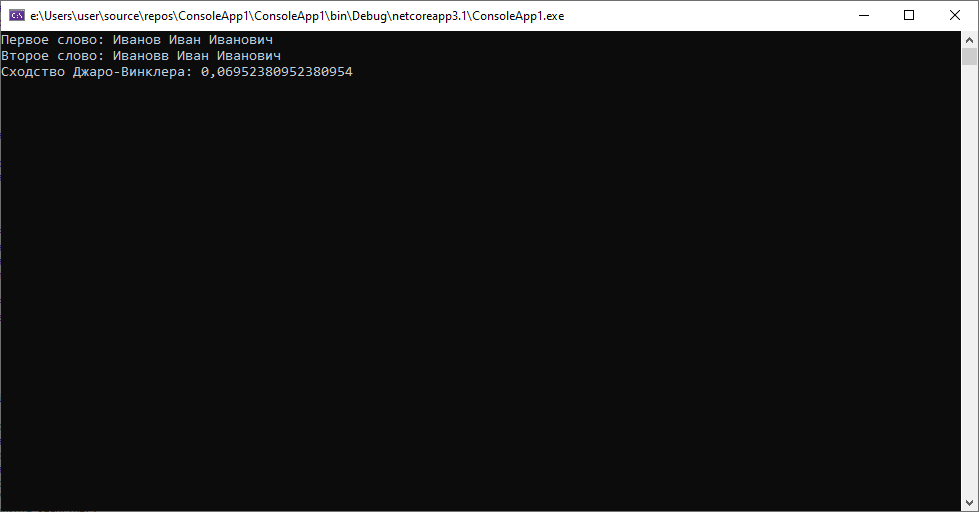
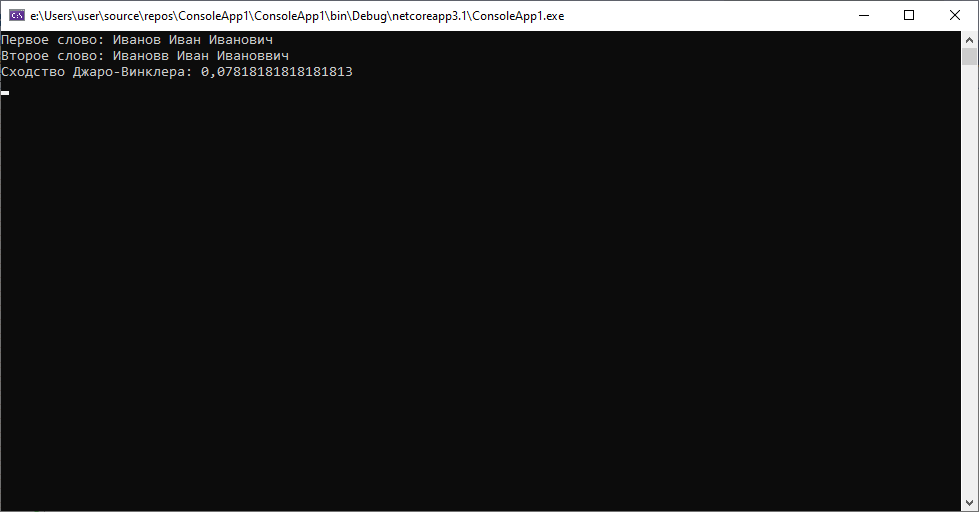
Как мы видим, во всех предложенных ситуациях алгоритм справляется на «отлично».
Настало время для контрольных примеров, когда мы заведомо знаем, что речь идет о разных людях.
1.Меняем фамилию
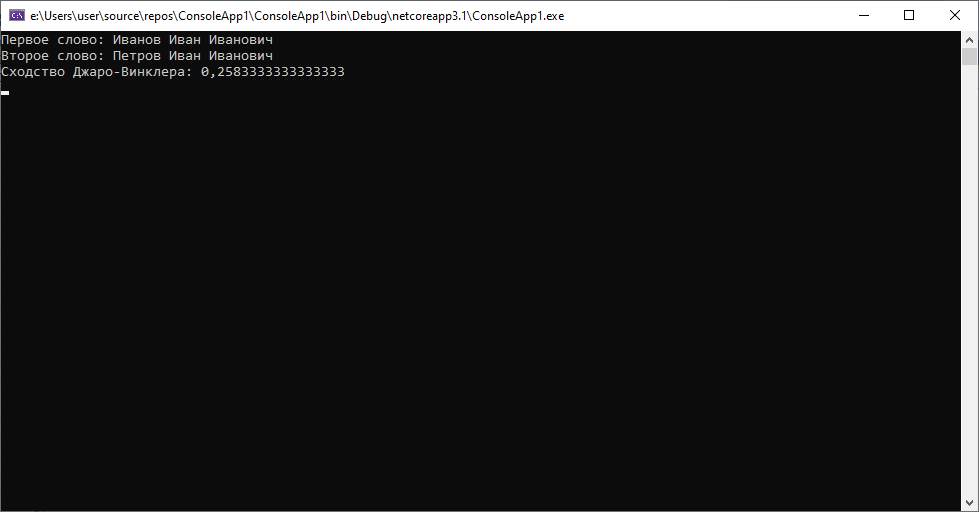
Люди с абсолютно разной фамилией, но при этом алгоритм не дает больших значений. Виной тому маленькая длина фамилии, относительно ФИО полностью. С более длинной фамилией ситуация бы немного выровнялась.
2.Попробуем еще немного поменять данные
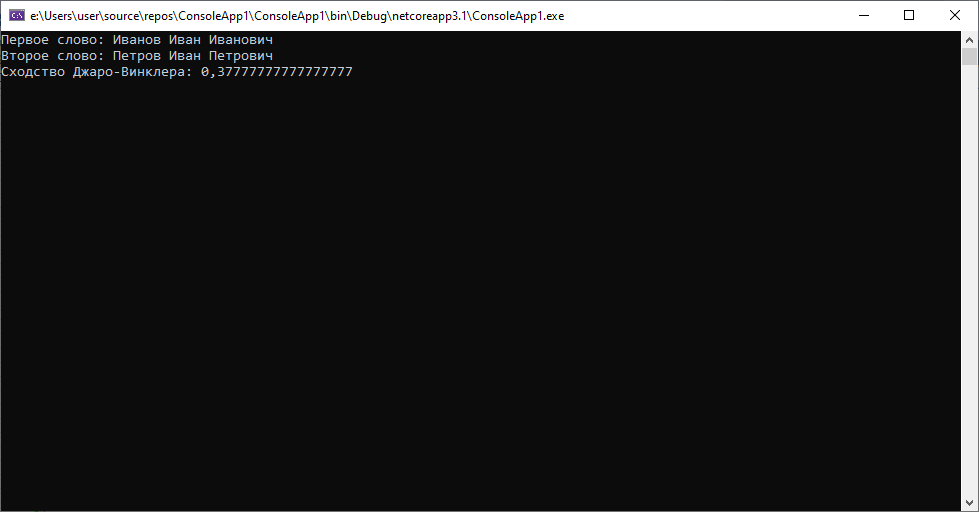
Снова таже история. Большого значения получить не удается, хотя этот результат выглядит намного лучше.
Выводы:
- Алгоритм достаточно хорошо справляется с большим количеством различных случаев «опечаток», несмотря на то что в нем учитываются в основном операции перестановки символов.
- Алгоритм не идеален и иногда «пасует» перед очевидными для человеческого глаза ошибками, но при этом раздельный анализ каждой из составляющих ФИО может прилично улучшить результаты.
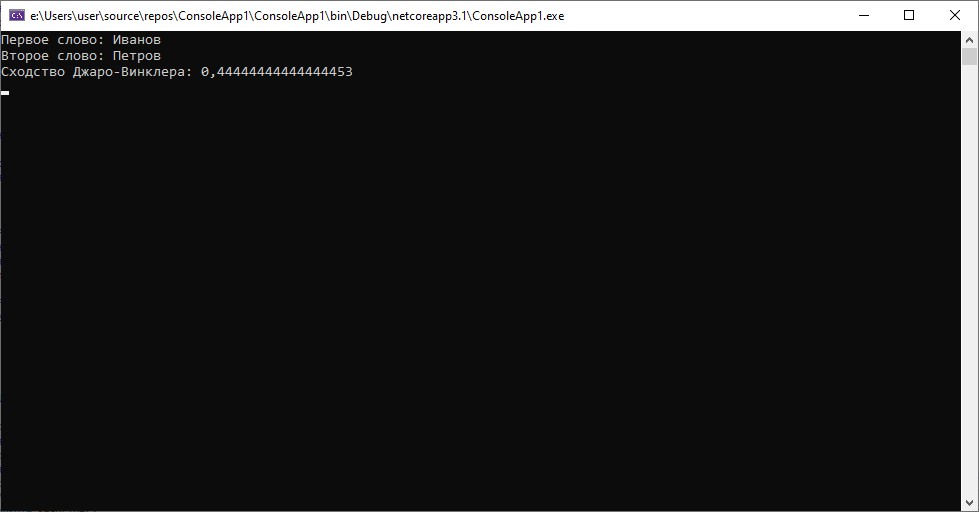
Если сравнивать только фамилии, ситуация становится намного яснее, даже при условии, что последние две буквы фамилий совпадают и фамилии небольшого размера и одинаковой длины.
В случае если фамилии отличаются сильнее, можно получить еще более внушительный результат:
Одним словом, если мы хотим работать с опечатками с применением этого алгоритма, есть смысл разбивать наши данные на логические фрагменты(например, в случае с ФИО отдельно фамилию, имя и отчество, в случае с ПД на серию и номер). При этом качество работы алгоритма будет достаточным для подавляющего количества случаев опечаток, с которыми мы можем встретиться. Вполне объяснимо, почему именно этот алгоритм применялся при обработке данных последней переписи населения.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
