Время прочтения: 9 мин.
Я занимался построением скоринговых карт в банке для самых разных продуктов и могу сказать, что жизненный цикл разработки стандартный. И цель этой заметки пройти цикл и построить скоринговую карту для оценки платежеспособности заёмщиков на основе данных из кредитной заявки.
Моделирование кредитных рисков
Моделирование кредитных рисков в банковский сектор пришло из ботаники. В статистике идеи классификации популяции на группы были разработаны Фишером в 1936 г. на примере растений. Этот тот самый знаменитый пример Ирисов Фишера. Он часто используется для иллюстрации работы статистических алгоритмов.
В 1941 г. Дэвид Дюран впервые применил данную методику к классификации кредитов на «плохие» и «хорошие». С началом Второй мировой войны банки столкнулись с необходимостью срочной замены аналитиков. Аналитики составили свод правил, которыми следовало руководствоваться при принятии решения о выдаче кредита, чтобы анализ мог проводиться неспециалистами. Это и был прообраз будущих систем принятия решения.
Таблица -1. Пример скоркарты 40-x годов.
| Параметр | Критерий оценки |
| Возраст | 0,1 балла за каждый год свыше 20 лет (максимум — 0,30) |
| Пол | женский (0,40), мужской (0) |
| Срок проживания в регионе | 0,042 за каждый год (максимально — 0,42) |
| Профессия | 0,55 за профессию с низким риском, 0 за профессию с высоким риском, 0,16 — другие профессии |
| Работа | 0,21 на предприятиях общественной отрасли, 0 — другие |
| Срок занятости | 0,059 за каждый год работы на данном предприятии |
| Финансовые показатели | 0,45 за наличие банковского счета, 0,35 за наличие недвижимости, 0,19 — за наличие полиса по страхованию |
Современные подходы к моделированию
Из-за требований внешних регуляторов в качестве моделей для скоринга кредитных заявок рассматриваются интерпретируемые модели. Например, решающее дерево или логистическая регрессия. Интерпретация решающего дерева простая и понятная. Визуализируйте.
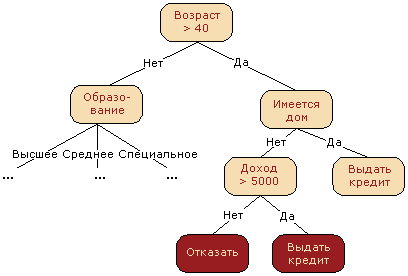
С интерпретацией логистической регрессии немного сложнее. Для этих целей и разрабатывается скоринговая карта.
Жизненный цикл разработки скоринговых карт
- Сбор, очистка и предобработка данных
- Монотонный WOE bining признаков
- Ручной WOE bining признаков при необходимости
- Отбор признаков по Information Value
- Построение логистической регрессии
- Построение скоркарты
Рассмотрим жизненный цикл на примере. Возьмём анонимизированный учебный набор данных по заявкам на кредитные карты — Credit Approval Data Set. К сожалению, нам не известны наименование признаков, но можем предположить, что туда входят возраст, пол, доход и т.д. Набор данных состоит из 14 признаков и целевой переменной. Предобработка данных в этом датасете очень простая. Заменим все «?» на NaN, а потом пропуски в числовых признаках на средние значения и на самое часто встречаемое в категориальных признаках.
df = pd.read_csv('crx.data', header=None, decimal=".")
df.columns = ['A' + str(i) for i in range(1, 16)] + ['target']
y = df.target
df = df.replace(to_replace='?',value=np.nan)
df.fillna(df.mean(), inplace=True)
for col in df.columns:
if df[col].dtypes == 'object':
df = df.fillna(df[col].value_counts().index[0])
categorical_columns = [c for c in df.columns if df[c].dtype.name == 'object']
numerical_columns = [c for c in df.columns if df[c].dtype.name != 'object']
print (categorical_columns)
print (numerical_columns)
Монотонный WOE binning признаков
Теперь необходимо написать WOE binning для числовых и категориальных переменных.
WOE считается для каждого признака!
Плюсы монотонного WOE binningа признаков:
- Упрощает интерпретацию
- Обрабатывает отсутствующие значения
- Выявляет сложные нелинейные связи
- Преобразование основано на логарифмическом распределении
- Упрощает обработку выбросов
- Нет необходимости в dummy variables
- Можно устанавливать монотонную зависимость (либо увеличение, либо уменьшение) между независимой и зависимой переменной
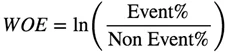
max_bin = 20
force_bin = 3
def mono_bin(Y, X, n = max_bin):
df1 = pd.DataFrame({"X": X, "Y": Y})
justmiss = df1[['X','Y']][df1.X.isnull()]
notmiss = df1[['X','Y']][df1.X.notnull()]
r = 0
while np.abs(r) < 1:
try:
d1 = pd.DataFrame({"X": notmiss.X, "Y": notmiss.Y, "Bucket": pd.qcut(notmiss.X, n)})
d2 = d1.groupby('Bucket', as_index=True)
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
n = n - 1
except Exception as e:
n = n - 1
if len(d2) == 1:
n = force_bin
bins = algos.quantile(notmiss.X, np.linspace(0, 1, n))
if len(np.unique(bins)) == 2:
bins = np.insert(bins, 0, 1)
bins[1] = bins[1]-(bins[1]/2)
d1 = pd.DataFrame({"X": notmiss.X, "Y": notmiss.Y, "Bucket": pd.cut(notmiss.X, np.unique(bins),include_lowest=True)})
d2 = d1.groupby('Bucket', as_index=True)
d3 = pd.DataFrame({},index=[])
d3["MIN_VALUE"] = d2.min().X
d3["MAX_VALUE"] = d2.max().X
d3["COUNT"] = d2.count().Y
d3["EVENT"] = d2.sum().Y
d3["NONEVENT"] = d2.count().Y - d2.sum().Y
d3=d3.reset_index(drop=True)
if len(justmiss.index) > 0:
d4 = pd.DataFrame({'MIN_VALUE':np.nan},index=[0])
d4["MAX_VALUE"] = np.nan
d4["COUNT"] = justmiss.count().Y
d4["EVENT"] = justmiss.sum().Y
d4["NONEVENT"] = justmiss.count().Y - justmiss.sum().Y
d3 = d3.append(d4,ignore_index=True)
d3["EVENT_RATE"] = d3.EVENT/d3.COUNT
d3["NON_EVENT_RATE"] = d3.NONEVENT/d3.COUNT
d3["DIST_EVENT"] = d3.EVENT/d3.sum().EVENT
d3["DIST_NON_EVENT"] = d3.NONEVENT/d3.sum().NONEVENT
d3["WOE"] = np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["IV"] = (d3.DIST_EVENT-d3.DIST_NON_EVENT)*np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["VAR_NAME"] = "VAR"
d3 = d3[['VAR_NAME','MIN_VALUE', 'MAX_VALUE', 'COUNT', 'EVENT', 'EVENT_RATE', 'NONEVENT', 'NON_EVENT_RATE', 'DIST_EVENT','DIST_NON_EVENT','WOE', 'IV']]
d3 = d3.replace([np.inf, -np.inf], 0)
d3.IV = d3.IV.sum()
return(d3)
def char_bin(Y, X):
df1 = pd.DataFrame({"X": X, "Y": Y})
justmiss = df1[['X','Y']][df1.X.isnull()]
notmiss = df1[['X','Y']][df1.X.notnull()]
df2 = notmiss.groupby('X',as_index=True)
d3 = pd.DataFrame({},index=[])
d3["COUNT"] = df2.count().Y
d3["MIN_VALUE"] = df2.sum().Y.index
d3["MAX_VALUE"] = d3["MIN_VALUE"]
d3["EVENT"] = df2.sum().Y
d3["NONEVENT"] = df2.count().Y - df2.sum().Y
if len(justmiss.index) > 0:
d4 = pd.DataFrame({'MIN_VALUE':np.nan},index=[0])
d4["MAX_VALUE"] = np.nan
d4["COUNT"] = justmiss.count().Y
d4["EVENT"] = justmiss.sum().Y
d4["NONEVENT"] = justmiss.count().Y - justmiss.sum().Y
d3 = d3.append(d4,ignore_index=True)
d3["EVENT_RATE"] = d3.EVENT/d3.COUNT
d3["NON_EVENT_RATE"] = d3.NONEVENT/d3.COUNT
d3["DIST_EVENT"] = d3.EVENT/d3.sum().EVENT
d3["DIST_NON_EVENT"] = d3.NONEVENT/d3.sum().NONEVENT
d3["WOE"] = np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["IV"] = (d3.DIST_EVENT-d3.DIST_NON_EVENT)*np.log(d3.DIST_EVENT/d3.DIST_NON_EVENT)
d3["VAR_NAME"] = "VAR"
d3 = d3[['VAR_NAME','MIN_VALUE', 'MAX_VALUE', 'COUNT', 'EVENT', 'EVENT_RATE', 'NONEVENT', 'NON_EVENT_RATE', 'DIST_EVENT','DIST_NON_EVENT','WOE', 'IV']]
d3 = d3.replace([np.inf, -np.inf], 0)
d3.IV = d3.IV.sum()
d3 = d3.reset_index(drop=True)
return(d3)
def data_vars(df1, target):
stack = traceback.extract_stack()
filename, lineno, function_name, code = stack[-2]
vars_name = re.compile(r'\((.*?)\).*$').search(code).groups()[0]
final = (re.findall(r"[\w']+", vars_name))[-1]
x = df1.dtypes.index
count = -1
for i in x:
if i.upper() not in (final.upper()):
if np.issubdtype(df1[i], np.number) and len(Series.unique(df1[i])) > 2:
conv = mono_bin(target, df1[i])
conv["VAR_NAME"] = i
count = count + 1
else:
conv = char_bin(target, df1[i])
conv["VAR_NAME"] = i
count = count + 1
if count == 0:
iv_df = conv
else:
iv_df = iv_df.append(conv,ignore_index=True)
iv = pd.DataFrame({'IV':iv_df.groupby('VAR_NAME').IV.max()})
iv = iv.reset_index()
return(iv_df,iv)
final_iv, IV = data_vars(df,y)

Объединим категории с близкими значениями WOE в одну категорию так, чтобы максимизировать разницу между группами. Теперь можно посмотреть на графиках, как переменные разбились по группам и проверить монотонность возрастает или убывает.
def plot_bin(ev, for_excel=False):
ind = np.arange(len(ev.index))
width = 0.35
fig, ax1 = plt.subplots(figsize=(10, 7))
ax2 = ax1.twinx()
p1 = ax1.bar(ind, ev['NONEVENT'], width, color=(24/254, 192/254, 196/254))
p2 = ax1.bar(ind, ev['EVENT'], width, bottom=ev['NONEVENT'], color=(246/254, 115/254, 109/254))
ax1.set_ylabel('Event Distribution', fontsize=15)
ax2.set_ylabel('WOE', fontsize=15)
plt.title(list(ev.VAR_NAME)[0], fontsize=20)
ax2.plot(ind, ev['WOE'], marker='o', color='blue')
plt.legend((p2[0], p1[0]), ('bad', 'good'), loc='best', fontsize=10)
q = list()
for i in range(len(ev)):
try:
mn = str(round(ev.MIN_VALUE[i], 2))
mx = str(round(ev.MAX_VALUE[i], 2))
except:
mn = str((ev.MIN_VALUE[i]))
mx = str((ev.MAX_VALUE[i]))
q.append(mn + '-' + mx)
plt.xticks(ind, q, rotation='vertical')
for tick in ax1.get_xticklabels():
tick.set_rotation(60)
plt.show()
def plot_all_bins(iv_df):
for i in [x.replace('WOE_','') for x in X_train.columns]:
ev = iv_df[iv_df.VAR_NAME==i]
ev.reset_index(inplace=True)
plot_bin(ev)
plot_all_bins(final_iv)
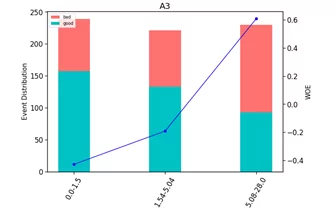
Далее оценим по графикам, монотонно возрастают или убывают. При необходимости провести ручной бининг. Ручной бининг нужен для объединения категорий с близкими значениями WOE в одну категорию так, чтобы максимизировать разницу между группами.
Отбор признаков по Information Value
Information Value (IV) измеряет предсказательную силу признаков. Считается для каждого признака.
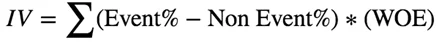
Значения Information Value (IV) для определения cutoff по отбору признаков:
- <0.02 Бесполезно для предсказания
- 0.02 – 0.1 Слабая
- 0.1 – 0.3 Средняя
- 0.3 – 0.5 Хорошая
- 0.5+ Слишком хорошо, что бы быть правдой
План отбора признаков по IV:
- Определить Cutoff для IV и корреляции
- Можно сразу исключить признаки с низким Information Value, а затем и по cutoff
- Осуществить проверку на корреляцию. Из двух коррелирующих признаков нужно исключить тот, у которого IV меньше
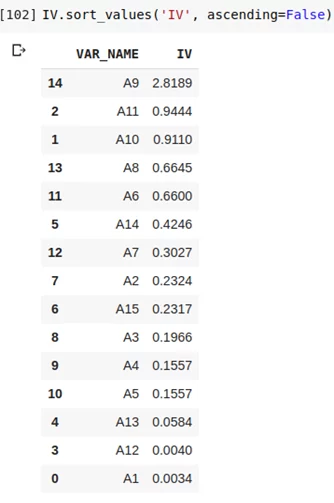
Построение логистической регрессии
Строим логистическую регрессию и оцениваем метрики на кросс-валидации и тестовой выборке. Смотрим на коэффициент ROC AUC или Gini.
import scikitplot as skplt
import eli5
def plot_score(clf, X_test, y_test, feat_to_show=30, is_normalize=False, cut_off=0.5):
print ('ROC_AUC: ', round(roc_auc_score(y_test, clf.predict_proba(X_test)[:,1]), 3))
print ('Gini: ', round(2*roc_auc_score(y_test, clf.predict_proba(X_test)[:,1]) - 1, 3))
print ('F1_score: ', round(f1_score(y_test, clf.predict(X_test)), 3))
print ('Log_loss: ', round(log_loss(y_test, clf.predict(X_test)), 3))
print ('\n')
print ('Classification_report: \n', classification_report(pd.Series(clf.predict_proba(X_test)[:,1]).apply(lambda x: 1 if x>cut_off else 0), y_test))
skplt.metrics.plot_confusion_matrix(y_test, pd.Series(clf.predict_proba(X_test)[:,1]).apply(lambda x: 1 if x>cut_off else 0), title="Confusion Matrix",
normalize=is_normalize,figsize=(8,8),text_fontsize='large')
display(eli5.show_weights(clf, top=20, feature_names = list(X_test.columns)))
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
for col in df.columns:
if df[col].dtypes=='object':
df[col]=le.fit_transform(df[col])
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
rescaledX_train = scaler.fit_transform(X_train)
rescaledX_test = scaler.fit_transform(X_test)
X_train, X_test, y_train, y_test = train_test_split(df, y, test_size=0.33, stratify=y, random_state=42)
clf_lr = LogisticRegressionCV(random_state=1, cv=7)
clf_lr.fit(X_train, y_train)
plot_score(clf_lr, X_test, y_test, cut_off=0.5)
Построение скоркарты — масштабирование баллов
Скорбалл считается по следующей формуле:
Score = (β×WoE+ α/n)×Factor + Offset
где:
β — коэффициент логистической регрессии признака
α — свободный член
WoE — Weight of Evidence признака
n — количество признаков, включенных в модель
Factor, Offset — параметры масштабирования. Множитель и смещение.
Множитель и смещение считаются так:
Factor = pdo/Ln(2) Offset = B — (Factor × ln(Odds))
где:
pdo — количество баллов, удваивающее шансы
B — значение на шкале баллов, в которой соотношение шансов составляет С:1
Например: Если скоринговая карта имеет базовые коэффициенты 50 : 1 в 600 баллах, а pdo из 20 (вероятность удвоения каждые 20 баллов), то множитель и смещение будут: Factor = 20/Ln(2) = 28.85 Offset = 600- 28.85 × Ln (50) = 487.14
coefficients = pd.DataFrame({"Feature":X_train.columns,"Coefficients":np.transpose(clf_lr.coef_[0] )})
print(coefficients.head(10))
print(clf_lr.intercept_)
beta = coefficients[coefficients['Feature']=='A3'].Coefficients.iloc[0]
alpha = 0
n = X_train.shape[1]
import math
factor = 40/math.log(2)
offset = 600 -57.7 * math.log(50)
o = offset/n
beta = 0.2
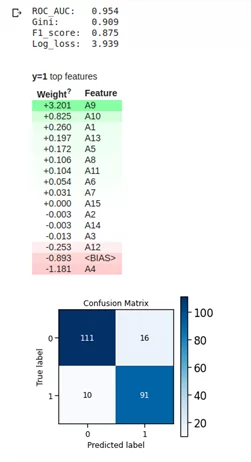
for kk in final_iv[final_iv['VAR_NAME']=='A3'].WOE:
ll = round(beta*kk+alpha/n,3)
tt=ll*factor
score = tt + o
print(round(score))
print(final_iv[final_iv['VAR_NAME']=='A3'])
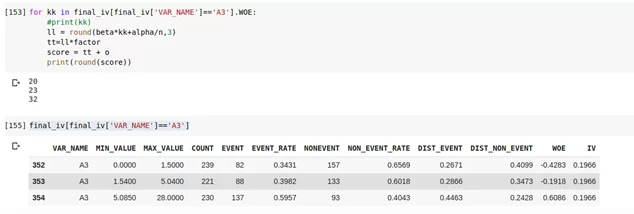
Получаем следующие скорбаллы:
- А3 от 0 до 1.5 : 20 баллов
- А3 от 1.54 до 5.04 : 23 балла
- А3 от 5.085 до 28 : 32 балла
Таким образом скорбаллы считаются и для остальных признаков и составляется итоговая скоркарта. Дополнительный плюс этого подхода, что потом реализовать готовую скоркарту можно на любом языке программирования, в любой системе используя конструкцию if else.
Полный код — https://colab.research.google.com/drive/1-a6ziABBVusCRZS5Mp2qkc-MszbjBdh1?usp=sharing
Канал автора статьи в телеграме https://t.me/renat_alimbekov

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)