Время прочтения: 4 мин.
Кодирование и декодирование информации. Каждый раз, когда мы слышим про эти термины, то представляем последовательность символов, взглянув на которые — сложно что-либо понять. Используется этот подход для защиты информации.
А что, если я вам расскажу, что кодировка и декодировка используется для отправки информации на дальние расстояния. Звучит тоже немного странно, но предлагаю разобраться в этой теме поподробнее.
Когда люди только начали запускать различных дронов на дальние расстояния в Космос — не было возможности возвращать их обратно на Землю для получения и изучения добытой информации. Как говорится — «Это экономически невыгодно». Поэтому информацию, полученную с помощью дронов, решили отправлять по радиосвязи. Но первый такой опыт тоже был неудачным. Причина — отправленная информация подвергалась шумовому воздействию (например: фотографии выглядели совсем неинформативно).

Кажется, данную проблему решить невозможно, однако, это ошибочное заблуждение. Решением будет использование кода Рида-Маллера. Основная суть метода заключается в переведении отправленной информации в двоичную систему, потом умножение на порождающую матрицу, что в свою очередь увеличивает количество битов, выделенное на хранение одного символа. И в конечном итоге — данные, подверженные шумовому наложению, можно раскодировать с помощью голосования после умножения на проверочную матрицу. Этот подход также называется методом мажоритарного декодирования.
В этой статье я хочу показать применение этого алгоритма для декодирования обычных текстовых сообщений. Первым делом нужно определить какой алфавит будет использоваться. В моем случае он выглядит так:
#Алфавит
alph = 'АБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЭЮЯабвгдеёжзийклмнопрстуфхцчшщъыьэюя0123456789.,!?;:№\'"(){}[]\\|/=+-*%^&$#@<>–—‘_`~«» '
В него я включила русский алфавит в верхнем и нижнем регистре, цифры и самые часто встречающиеся символы. Тут важно помнить, что размер алфавита лучше делать примерно равным двойке, возведенной в какую-либо степень. Все потому, что алфавит нужно будет перекодировать в двоичную систему счисления. Это и будет вторым шагом.
#Словарь буква: позиция буквы в битовом виде
d1 = {a: [int(i) for i in f'{alph.index(a):07b}'] for a in alph}
С помощью данной конструкции мы записываем наш словарь в виде ключа. Где ключ — это символ, а соответствующий ему код записан в двоичной системе счисления. Пример можете увидеть на картинке ниже.

Теперь нужно объявить порождающую матрицу, она выглядит следующим образом:
#Порождающая матрица
gm = np.array([
[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1],
[0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1],
[0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1,0,0,0,0,1,1,1,1],
[0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1,0,0,1,1],
[0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1],
])
В итоге — для увеличения длины выделенных битов на один символ нам нужно каждый ключ из нашего алфавита умножить на порождающую матрицу. В итоге получается уникальная последовательность символов с длинной 64.
Следующим шагом я реализовала функцию наложения шумов и назвала её — noise. В рандомном месте по длине закодированного символа меняем 1 на 0 и наоборот.
#Функция помех
def noise(arr,max_errors):
d=list(arr)
for i in range(max_errors):
pos = random.choice(range(63))
d[pos] = (1+d[pos]) % 2
return d
Проверочная матрица является прототипом проверочных уравнений, для её создания можно использовать цикл, количество шагов равно необходимому количеству нужных проверочных уравнений. Функцию проверки (умножение на проверочную матрицу) я назвала sistem, так как практическим смыслом является решение системы уравнений.
# функция для решения систем уравнений
def sistem(с2,e_noisy):
c2 = np.array([np.zeros(32, int) for i in range(6)])
# создание матрици коэффициентов для проверочных уравнений
for i in range(len(c1)):
k = 0
for j in range(len(c1[i])-1):
if c1[i][j] != c1[i][j+1]:
k = k+1
c2[i][j+1] = k
else:
c2[i][j+1] = k
for i in range(len(c2)):
for j in range(len(c2[i])):
c3[i][j] = (e_noisy[j+2**(5-i)*c2[i][j]] +
e_noisy[j+2**(5-i)*c2[i][j]+2**(5-i)]) % 2
return c3Осталось применить метод мажоритарного декодирования, для которого функция будет выглядеть так:
# функция голосования
def golos(c3):
v = []
for i in range(len(c3)):
n0 = 0
n1 = 0
for j in range(len(c3[i])):
if c3[i][j] == 0:
n0 = n0+1
else:
n1 = n1+1
if n0 > n1:
v.append(0)
else:
v.append(1)
return v
После выполнения этого шага нам возвращается «нормальная» кодировка символа, которую мы может декодировать в букву нашего алфавита.
#Функция декодирования для символа
def decode(s):
return list(d1.keys())[list(d1.values()).index(s)]
Если показывать результат в обычном выводе в консольке, то это будет выглядеть очень скучно, поэтому я реализовала использование всех этих функции в программе с графическим интерфейсом с помощью библиотеки wx.
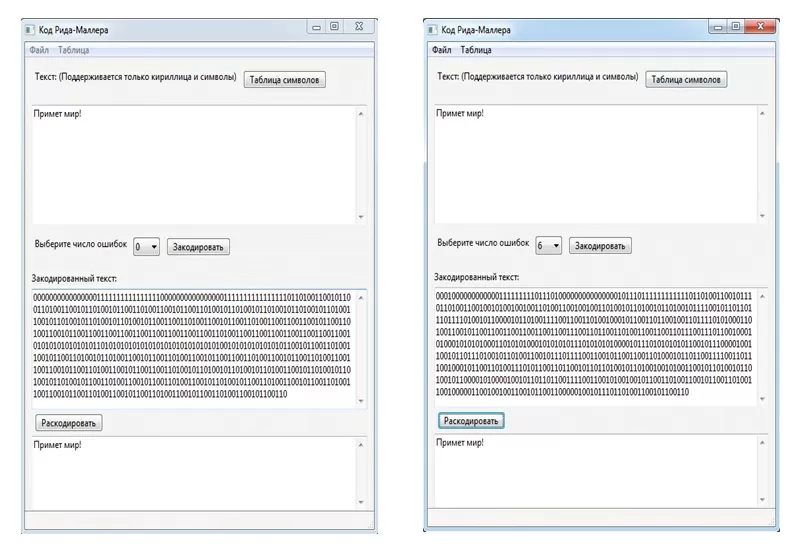
На первом примере программа успешно декодировала текст без помех, а на втором: количество ошибок — 6 и декодирование тоже прошло успешным образом.
Для более подробного изучения этого алгоритма советую почитать статью И. В. Агафонова «КОДЫ РИДА–МАЛЛЕРА: ПРИМЕРЫ ИСПРАВЛЕНИЯ ОШИБОК». Ну, а если хотите увидеть подробный разбор создания приложения с графическим интерфейсом на Python, то оставляй свой комментарий с пожеланиями.

/img/star (2).png.webp)
/img/news (2).png.webp)
/img/event.png.webp)
