Расстояние Хэмминга

Время прочтения: 4 мин.

Установление степени сходства между текстами – задача, которая часто встречается в повседневной работе. В частности данный подход может пригодится при нечетком поиске, при работе с данными с возможными погрешностями(например, если данные «восстанавливаются» их распознанного документа или), а также при работе с персональными данными, качество которых, зачастую, зависит от человеческого фактора. Ранее мы уже рассматривали один из наиболее эффективных алгоритмов для сравнения двух последовательностей символов, применительно к возможным опечаткам в ФИО (расстояние Левенштейна — ссылка, схожество Джаро — Винклера — ссылка). Сегодня поговорим о другом способе вычисления редакционного расстояния и о кейсах, в которых он может быть наиболее применимым.

Расстояние Хэмминга

Один из самых простых подходов к вычислению дистанции между строками. Это число позиций, в которых соответствующие символы двух слов одинаковой длины различны. Изначально использовалось для определения меры различия между кодовыми комбинациями (двоичными векторами) в векторном пространстве кодовых последовательностей. Еще раз обратим внимание, что данный алгоритм применим только для строк одинаковой длины, при вычислении расстояния строки посимвольно сравниваются, и число «несовпадающих» символов и будет нашим результатом.

На языке программирования C# реализация будет выглядеть так:

        public static int GetHammingDistance(string firstWord, string secondWord)
        {
            if (firstWord.Length != secondWord.Length)
            {
                throw new Exception("Strings must be equal length");
            }
            char[] c1 = firstWord.ToCharArray();
            char[] c2 = secondWord.ToCharArray();
            int distance = 0;
            int i = 0;
            while (i < c1.Length)
            {
                if (c1[i] != c2[i]) { distance++; }
                i++;
            }

Или с использование LINQ вот так:

public static int GetHammingDistance(string firstWord, string secondWord)
        {
            if (firstWord.Length != secondWord.Length)
            {
                throw new Exception("Strings must be equal length");
            }

            int distance =
                firstWord.ToCharArray()
                .Zip(secondWord.ToCharArray(), (c1, c2) => new { c1, c2 })
                .Count(m => m.c1 != m.c2);

            return distance;
        }

Где можно применить данный алгоритм? Учитывая, что происходит банальное посимвольное сравнение, без учета операций перестановки, удаления, вставки символов, причем со строками одинаковой длины, данный алгоритм может пригодиться разве что при сравнении некоторых «условно-числовых» значений, которые могут встретиться среди персональных данных(например серия и номер паспорта, ИНН, номер счета, СНИЛС, номер водительского удостоверения), но даже при таком искусственном ограничении — не всегда. Рассмотрим пару кейсов:

1.Паспортные данные клиентов 1234 567890 и 1244 567890, полученные из разных источников(допустим одни данные из автоматизированной системы, а вторые  — распознанные данные со скана договора) для клиента Иванова Ивана Ивановича 01.01.1990. Для такой ситуации расстояние будет следующим:

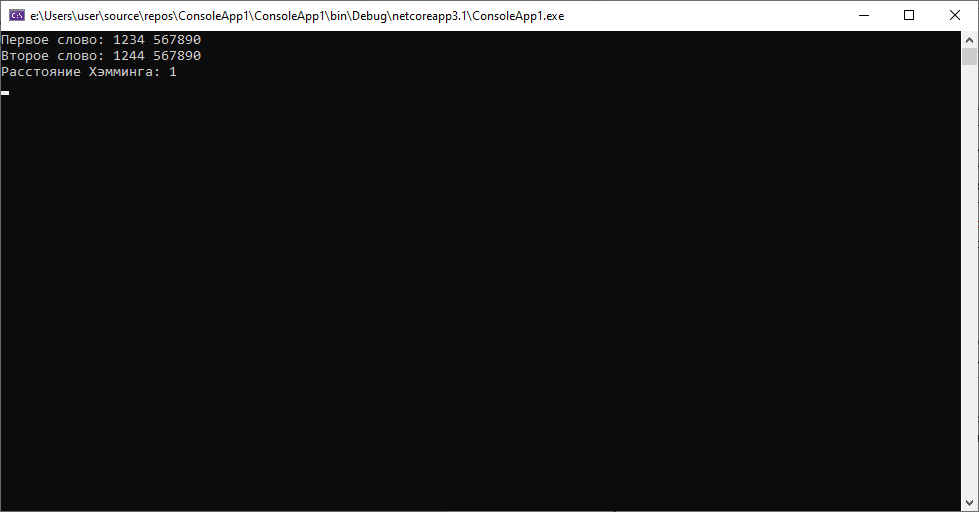
Как мы видим дистанция между строками небольшая, как и предполагалось, ведь они отличаются всего на один символ.

2.Предположим, что теперь наши данные таковы:  1234 567890 и 1243 567890(допустим, оба документа «пришли» к нам из разных автоматизированных систем). В данном случае алгоритм Хэмминга покажет следующее:

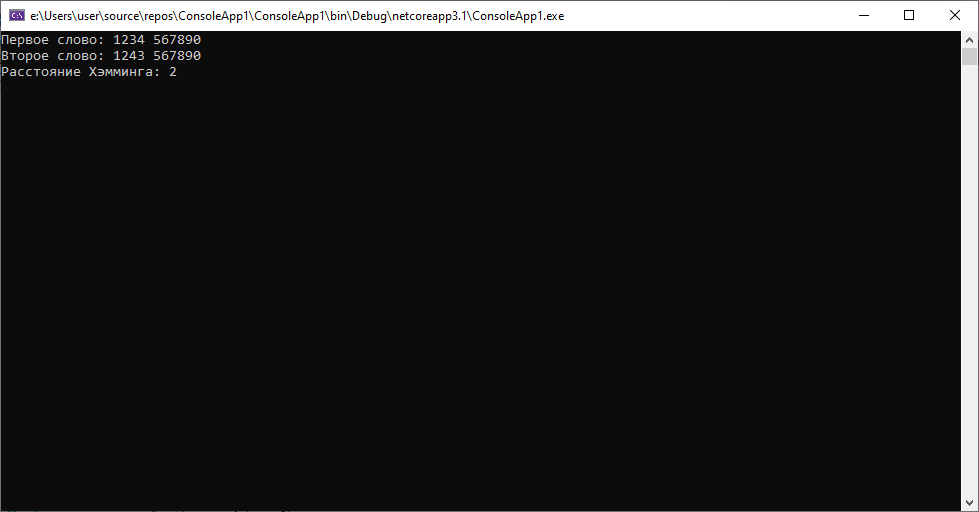
Здесь мы видим, что при минимальном различии(для нас очевидно, что в одном из случаев была «опечатка» — сотрудник неверно последовательно ввел 2 символа), расстояние уже будет равно 2. В то время, как при вычислении расстояния Левенштейна результат будет равен 1. Вывод: использование данного алгоритма для сравнения строк одинаковой длины возможно(и иногда уместно, учитывая простоту вычислений), но требует большего внимания при работе с данными, иногда расстояние может быть достаточно велико в случаях пропуска символов.

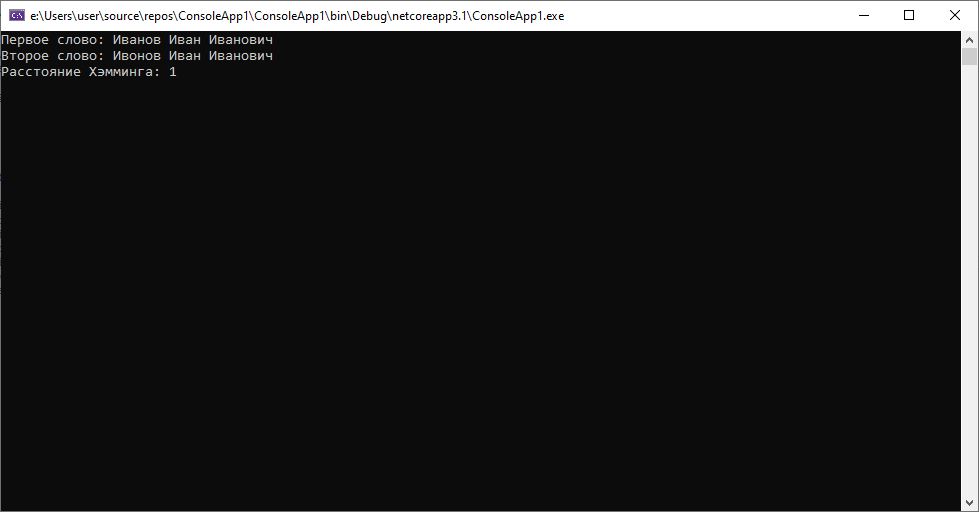
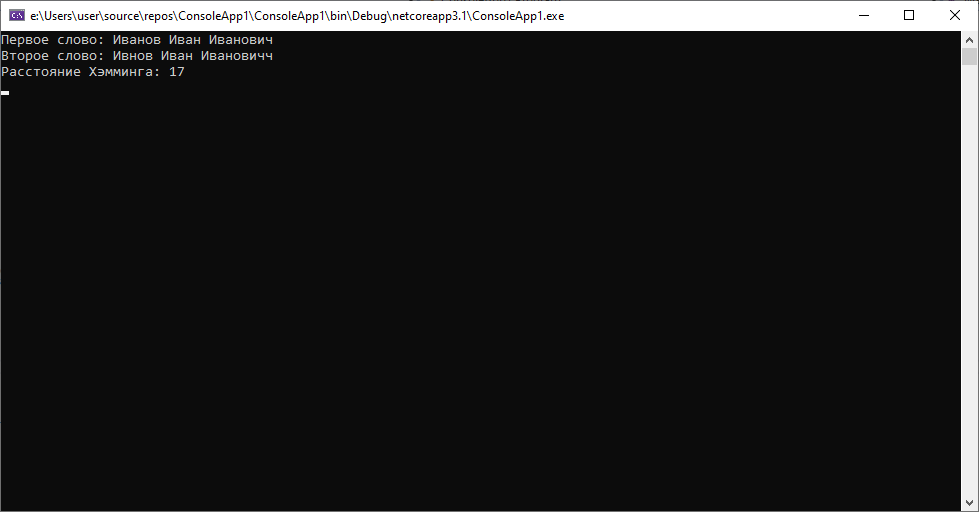
При этом расстояние Левенштейна во втором случае будет таковым.

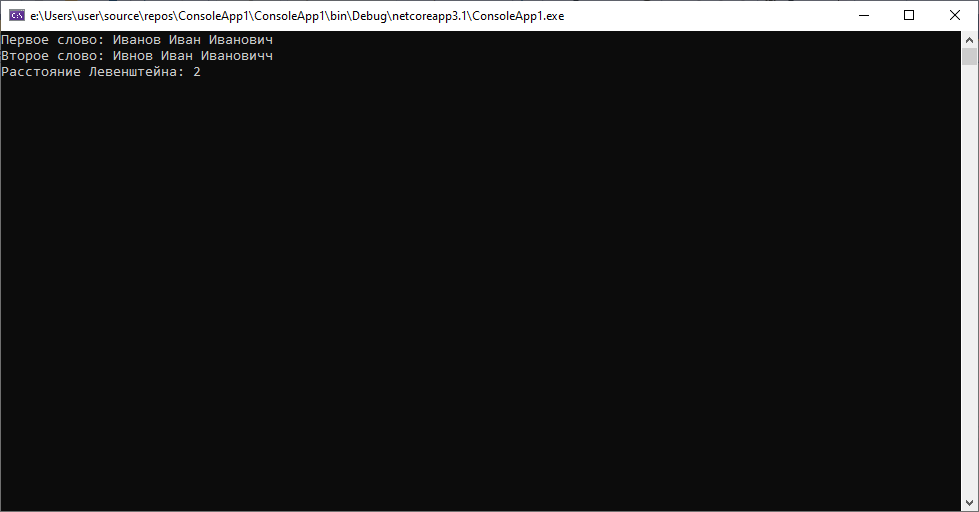
Выводы: В случае работы с ФИО лучше использовать расстояние Левенштейна, не говоря уже о том, что строки могут быть по разным причинам не одинаковой длины. Однако в случае обработки значений заведомо фиксированной длины с небольшим количеством опечаток, расстояние Хэмминга может быть неплохим выбором для решения задачи.