Время прочтения: 5 мин.
При проведении аудиторских проверок с использованием моделей машинного обучения одной из часто решаемых задач является задача кластеризации. Например, необходимо разбить на несколько кластеров отзывы клиентов на мобильное приложение (задача тематического моделирования). Для задач кластеризации часто используют модель k-means. Это обусловлено её простотой и понятностью. Однако, у этого алгоритма есть один большой недостаток — необходимость изначально задать число кластеров. Эта проблема прекрасно решается с помощью расширяющегося нейронного газа.
Расширяющийся нейронный газ строит граф, пытаясь приблизить распределение данных. Не связанные подграфы этого графа — это наши искомые кластеры. Он строится по следующему алгоритму:
- Генерация первых двух нейронов случайным образом
- На каждом шаге итерационного процесса берется один элемент данных. Два ближайших к нему нейрона двигаются в его сторону
- Между наиболее часто перемещающемуся нейроном и его ближайшим соседом создается новый нейрон
- Удаляются связи, если соединенные им нейроны вместе не передвигаются, и нейроны без связей
Рассмотрим этот итерационный алгоритм на примере со следующими данными:
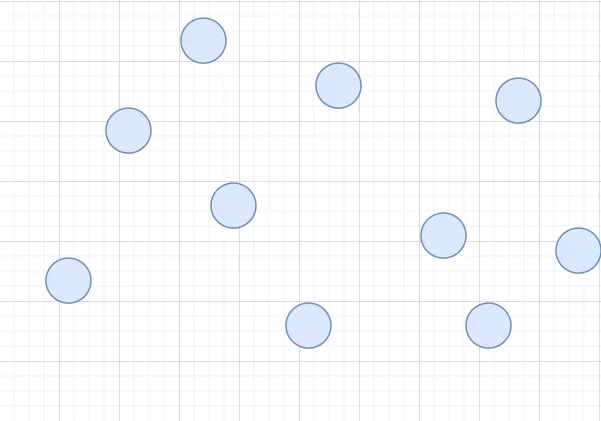
В самом начале построения графа случайным образом задаются первые два нейрона s1 и s2.
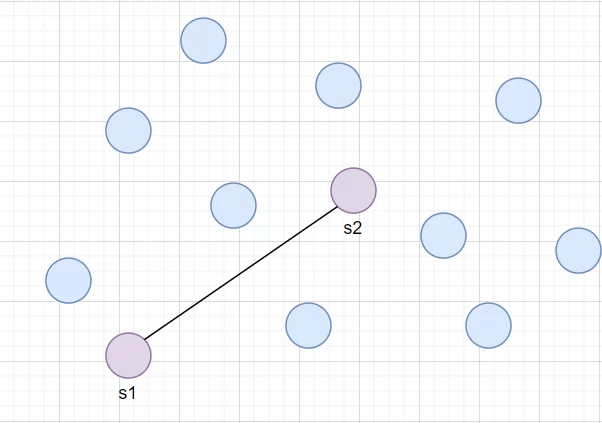
После этого начинается итерационный процесс:
- Выбирается один элемент наших данных v1.
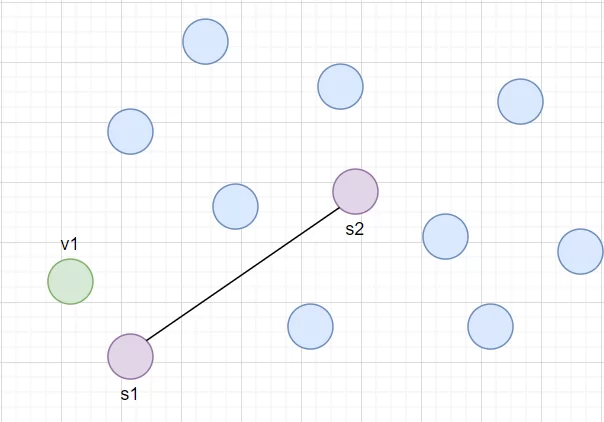
Выбирается два ближайших нейрона. Они перемещаются на r1 и r2 соответственно ближе к данному элементу, где r1 > r2.
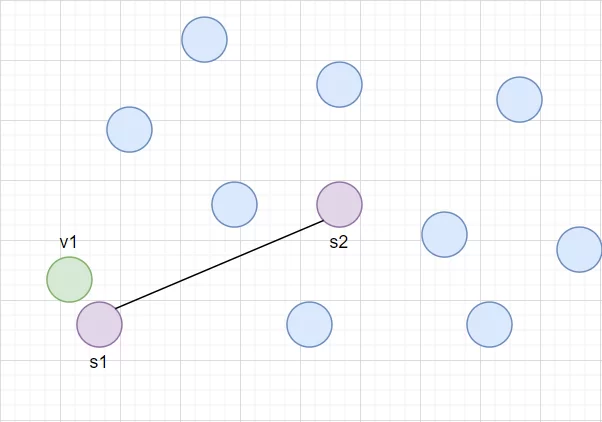
Следующие три итерации s2 поменяет свое местоположение сильнее, чем s1. Значит в окрестности s2 большая плотность данных, и нужно создать новый нейрон s3 посередине между s2 и его ближайшим соседом s1. Связь между s1 и s2 удаляется.
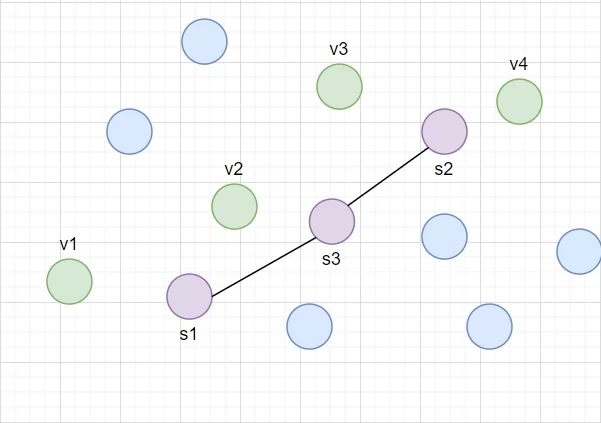
После еще 3 итераций нейрон s1 никаким образом не изменит своего положения. Значит он не помогает приблизить распределение наших данных. Сначала удаляется его связь с s3, а потом и он сам
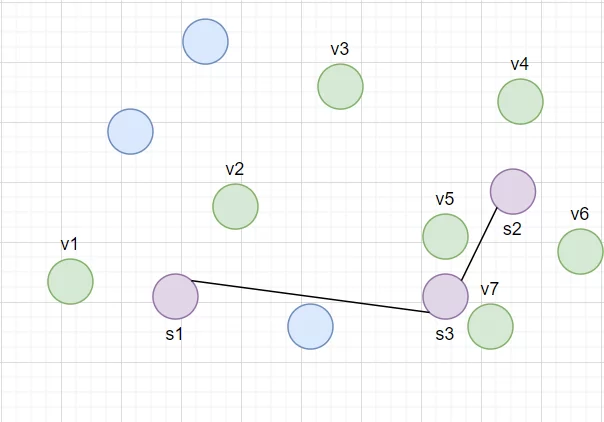
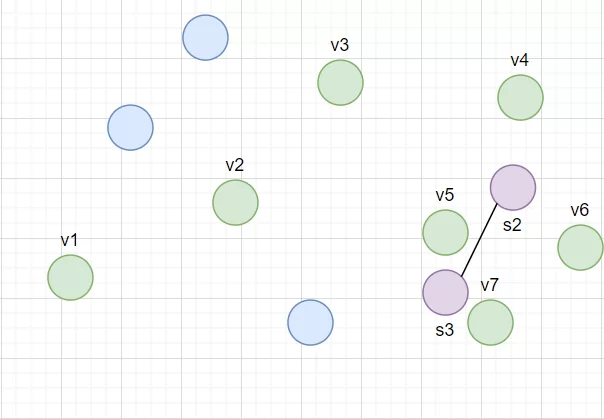
За следующие 3 итерации мы столкнемся с такой же проблемой, как в пункте 3 и нам понадобится создать s4. В результате получится граф s2-s3-s4, приближающий распределение наших данных
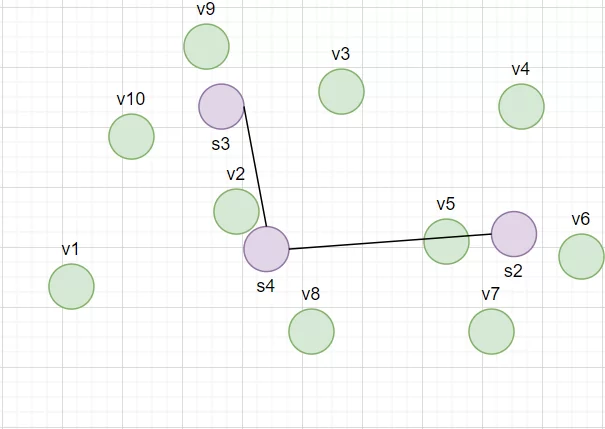
В результате получается граф с несколькими не связанными подграфами, повторяющие распределение наших данных. Их число можно использовать как искомое количество кластеров для k-means.
Эту гипотезу нужно проверить на реальных данных.
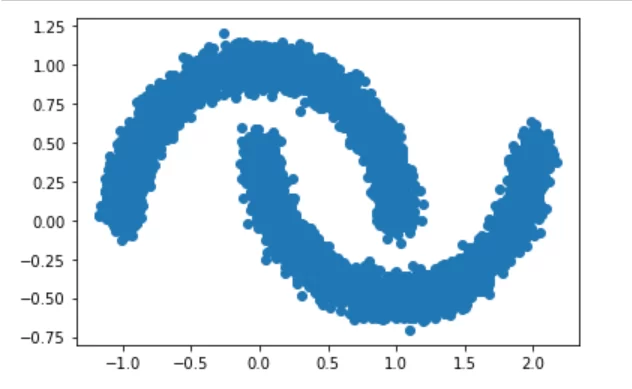
Для начала возьмем стандартный набор данных sklearn c двумя полумесяцами:
from sklearn.datasets import make_moons
data, _ = make_moons(10000, noise=0.06, random_state=0)
plt.scatter(*data.T)
plt.show()
Переобучением нам потребуется создать несколько своих функций для визуализации графа и подсчета несвязанных графов в нем:
import copy
from neupy import algorithms, utils
def draw_image(graph, show=True):
for node_1, node_2 in graph.edges:
weights = np.concatenate([node_1.weight, node_2.weight])
line, = plt.plot(*weights.T, color='black')
plt.setp(line, linewidth=0.2, color='black')
plt.xticks([], [])
plt.yticks([], [])
if show:
plt.show()
def create_gng(max_nodes, step=0.2, n_start_nodes=2, max_edge_age=50):
return algorithms.GrowingNeuralGas(
n_inputs=2,
n_start_nodes=n_start_nodes,
shuffle_data=True,
verbose=True,
step=step,
neighbour_step=0.005,
max_edge_age=max_edge_age,
max_nodes=max_nodes,
n_iter_before_neuron_added=100,
after_split_error_decay_rate=0.5,
error_decay_rate=0.995,
min_distance_for_update=0.01,
)
def extract_subgraphs(graph):
subgraphs = []
edges_per_node = copy.deepcopy(graph.edges_per_node)
while edges_per_node:
nodes_left = list(edges_per_node.keys())
nodes_to_check = [nodes_left[0]]
subgraph = []
while nodes_to_check:
node = nodes_to_check.pop()
subgraph.append(node)
if node in edges_per_node:
nodes_to_check.extend(edges_per_node[node])
del edges_per_node[node]
subgraphs.append(subgraph)
return subgraphs
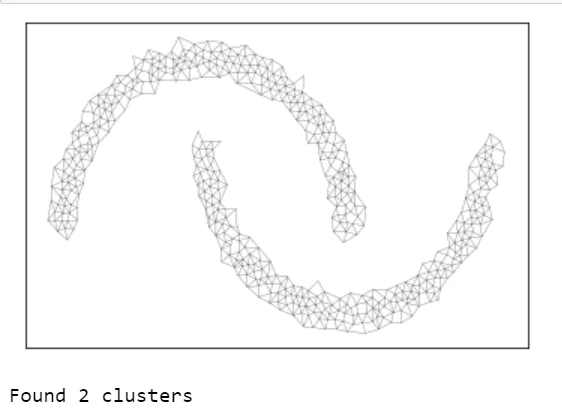
В результате обучения расширяющийся нейронный газ точно сохранил форму данных всего лишь с 500 элементами, хотя изначальный набор данных состоял из 10000, и точно определил, что здесь два кластера.
utils.reproducible()
gng = create_gng(max_nodes=500)
for epoch in range(20):
gng.train(data, epochs=1)
draw_image(gng.graph)
print("Found {} clusters".format(len(extract_subgraphs(gng.graph))))
К сожалению, такие хорошо структурированные данные редко встречаются в реальных задачах.
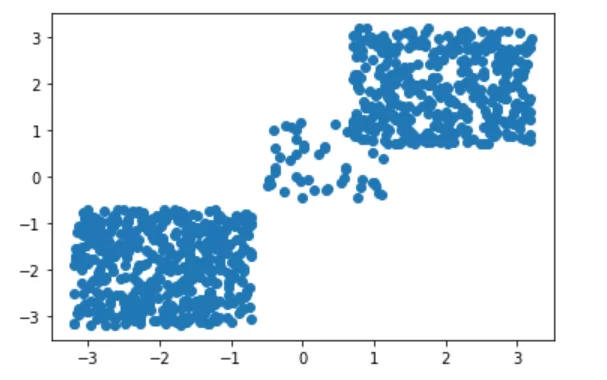
Для искусственной имитации реальной ситуации создадим набор данных с 3 кластерами со случайным образом разбросанными элементами:
X = -0.7 - 2.5 * np.random.rand(900,2)
X1 = 0.7 + 2.5 * np.random.rand(375,2)
X2 = -0.5 + 1.7 * np.random.rand(50,2)
X[475:850, :] = X1
X[850:900, :] = X2
plt.scatter(X[ : , 0], X[ :, 1])
plt.show()
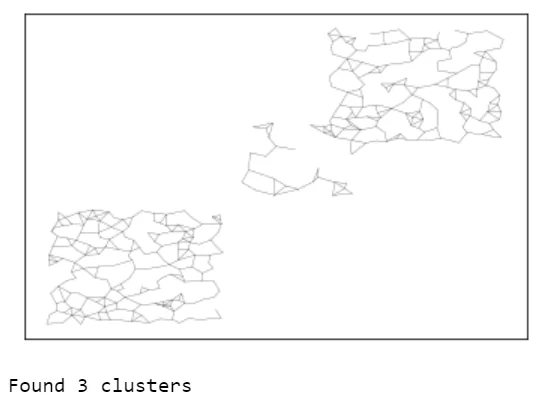
Несмотря на не структурированность данных и неявные границы между ними, расширяющийся нейронный газ и здесь смог правильно приблизить распределение и определить количество кластеров.
utils.reproducible()
gng = create_gng(max_nodes=300)
for epoch in range(40):
gng.train(X, epochs=1)
draw_image(gng.graph)
print("Found {} clusters".format(len(extract_subgraphs(gng.graph))))

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
