Время прочтения: 4 мин.
Каждый день люди сталкиваются с огромным количеством данных, но, несмотря на переход к электронному документообороту, встречаются документы, которые отсканированы человеком и содержат рукописный текст, в том числе цифры, даты, подписи и пр.
Распознавание рукописного текста – это огромная проблема, так как существует всего 10 цифр, а почерк человека может сильно варьироваться и порой с задачей распознания рукописного текста не справляется даже сам человек, что уж говорить о почерке врача 😊
Классификация рукописного текста или цифр очень важна на практике, это поможет сократить время на разбор огромного количества данных.
В этой статье я хочу рассмотреть распознавание рукописных цифр от 0 до 9, с использованием известного набора данных digits библиотеки Scikit-learn, применяя классификатор логистической регрессии.
Кратко о наборе данных digits
Область данных digits содержит некоторое множество наборов данных, которые могут быть полезны для тестирования задач анализа данных и прогнозирования результатов.
Для того, чтобы работать с распознаванием рукописного текста, вам понадобятся следующие библиотеки: matplotlib, sklearn, scipy
На примере встроенного набора данных библиотеки sklearn — digits рассмотрим выполнение распознавания цифр. Для этого импортируем его, чтобы начать использовать.
import sklearn.datasets
dd = datasets.load_digits()
print(dd.DESCR)

Область данных digits представляет собой словарь, в котором содержатся данные, целевые объекты, изображения, а также названия объектов и описание набора данных с названиями целевых объектов и пр.
Я ориентируюсь на наборе данных и целевой функции, извлечем два списка в две разные переменные.
m_d=dd['data']
tt=dd['target']
print(len(m_d))
import matplotlib.pyplot as pltt
%matplotlib inline
def show_cifr(index):
pltt.imshow(dd.images[index],cmap=pltt.cm.gray_r, interpolation='nearest')
pltt.title('Цифра: ' + str(dd.target[index]))
pltt.show()
show_cifr(8)
Давайте рассмотрим 3 модели: классификатор опорных векторов, классификатор деревьев решений и классификатор случайного леса, для того, чтобы понять, как работает каждая из моделей на одном наборе данных.
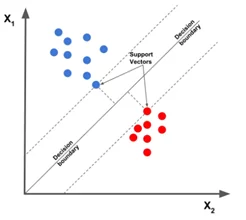
Классификатор опорных векторов
Задача этого алгоритма заключается в том, чтобы найти гиперплоскость в n-мерном пространстве, где n – это число признаков, чтобы проклассифицировать все точки данных.
from sklearn import svm
svm = svm.SVC(gamma = 0.001, C=100.)
svc.fit(m_d[:1790], tt[:1790])
pr = svc.predict(m_d[1791:])
pr, tt[1791:]
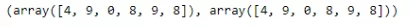
На выходе мы получили 100% совпадение, где 1791 значение используется для обучения, а 6 входных данных используются для тестирования.
Классификатор деревьев решений
В классификаторе дерева решений применяется простая идея решения задачи классифкации. Задается ряд тщательно продуманных вопросов об атрибутах тестовой записи. Каждый раз, когда будет задан вопрос – юна выходе получаем ответ до тех пор, пока не будет сделан вывод о классовой метке записи.
from sklearn.tree import DecisionTreeClassifier
dt = DecisionTreeClassifier(criterion = ‘gini’)
dt.fit(m_d[:1550] , tt[:1550])
pr2 = dt.predict(m_d[1551:]
import sklearn.metrics.accuracy_score
import sklearn.metrics.confusion_matrix
confusion_matrix(tt[1551:], pr2)

accuracy_score(tt[1551:], pr2)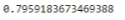
Как можно видеть, классификатор дерева решений плохо работает с данными. Вы можете попробовать повысить точность путем настройки гиперпараметров DTC.
Классификатор случайного леса
Случайный лес – является контролируемым алгоритмом обучения. Его используют как для классификации, так и для регрессии.
При случайном лесе можно создать деревья решений на случайно выбранных выборках набора данных и получают прогноз каждого дерева и в последствии выбирают лучшее решение с помощью голосования.
import sklearn.ensemble.RandomForestClassifier
rc = RandomForestClassifier(n_estimators = 150)
rc.fit(m_d[:1400], tt[:1400])
pr3 = rc.predict(m_d[1401:])
accurace_store(tt[1401:], pr3)
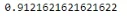
Таким образом, мы можем увидеть, что случайный лес отлично работает на меньшем количестве данных в сравнении с деревом решений. Оценка точности составляет 92%.
Согласно гипотезе, при настройке гиперпараметра с помощью различных моделей можно достичь более 96% точности распознавания рукописного набора данных. Но прежде необходимо убедиться, что тестовые данные будут хорошими, иначе модель может быть перегружена.
Удачи в кодировании! 😊

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
