Время прочтения: 7 мин.
Модель SIR
Одним из самых простых способов описания распространения болезни среди населения является SIR-модель. Она была представлена в 1920 году. С ее помощью можно легко смоделировать эпидемии в больших городах, а также анализировать разные варианты течения эпидемии.
SIR расшифровывается как:
S (Susceptible) – «восприимчивые», еще не переболевшие и подверженные заражению;
I (Infected) – «инфицированные», те, кто на данный момент болеет;
R (Resistant или Recovered) – «защищённые», те, кто выздоровели и больше не подвержены заражению или в некоторых модификациях модели (о которых я расскажу далее) просто «выздоровевшие».
SIR-модель также можно представить в виде графика перехода состояний.

В модели используются два коэффициента: коэффициент beta, показывает скорость заражения (перехода из восприимчивых в заражённые) и коэффициент gamma, он показывает скорость выздоровления (перехода из заражённых в выздоровевшие).
Математически модель SIR задаётся системой дифференциальных уравнений. В данном случае они говорят о том, что число восприимчивых, инфицированных и выздоровевших меняется с течением времени.
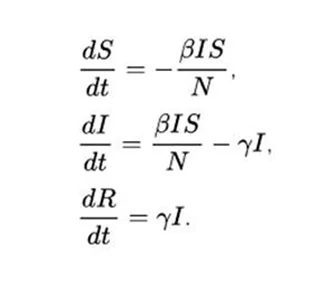
Действительно, в зависимости от коэффициентов скорости заражения и выздоровления число заражённых, инфицированных и выздоровевших меняется в течение времени таким образом, что общее число населения всегда постоянно и равно N = S + I + R.
Реализация модели SIR на Python
classSIR
def __init__(self, S, I, R, beta=0.05, gamma=0.01, epochs=365):
self.Susceptible = S
self.Infeлcted = I
self.Resistant = R
self.beta = beta
self.gamma = gamma
self.population = S + I + R
self.epochs = epochs
def start_simulation(self):
Susceptible = [self.Susceptible]
Infected = [self.Infected]
Resistant = [self.Resistant]
for epoch in range(1, self.epochs):
dS_dt = - (self.beta * Infected[-1] * Susceptible[-1]) / self.population
dI_dt = (self.beta * Infected[-1] * Susceptible[-1]) / self.population - self.gamma * Infected[-1]
dR_dt = self.gamma * Infected[-1]
Susceptible.append(Susceptible[-1] + dS_dt)
Infected.append(Infected[-1] + dI_dt)
Resistant.append(Resistant[-1] + dR_dt)
Комментарий: данную реализацию можно оптимизировать, здесь она для наглядности приведена в соответствие с системой уравнений.
При параметрах beta = 0.05 и gamma = 0.01 получается следующий график, на котором видно, как в случае появления заражённых вся популяция постепенно переходит в категорию инфицированных, а затем в категорию выздоровевших. В качестве показателей в данной модели используются S = 950 и I = 50.
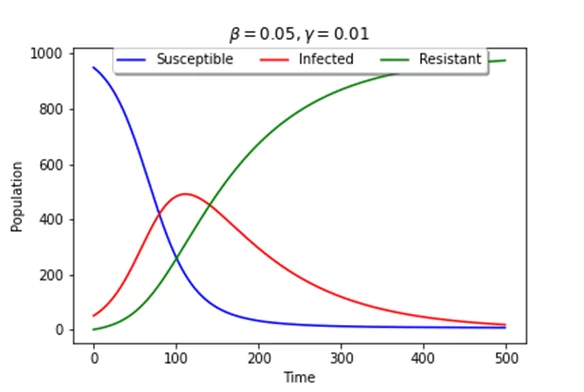
При увеличении beta этот переход осуществляется быстрее, а при увеличении gamma может получиться так, что не вся популяция переболеет и ее часть так и останется в группе восприимчивых, хотя инфицированных уже не будет (также возможен случай, при котором число выздоровевших будет меньше числа восприимчивых, этот случай говорит о том, что популяция быстрее выздоравливает, чем заражается).
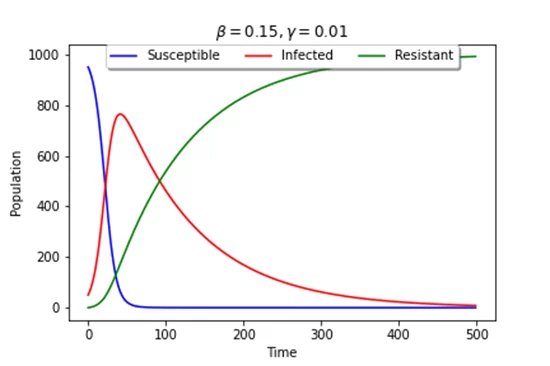
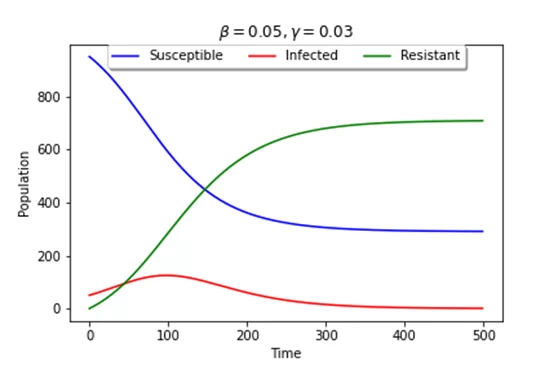
Модель SIR является самой простой моделью и описывает течение пандемии в так называемом «вакууме», не учитывая все важные параметры. Чтобы сгладить этот эффект вакуума и приблизить модель к более реалистичной, предлагаем рассмотреть несколько модификаций.
Модификации модели SIR
Например, в модификации, называемой SEIR появляется дополнительная категория Exposed, которая обозначает то, что заболевание находится в инкубационном периоде.
Также есть ее расширенная модификация SEIRD, где добавляется категория Dead, показывающая сколько человек всего умерло за время пандемии. При добавлении этих категорий в модель добавляются дополнительные параметры (такие как beta и gamma в основной SIR-модели), характеризующие возможность перехода из восприимчивых в инкубационные и из заражённых в умершие.
Еще одной модификацией является модель SIS, в которой инфицированный после выздоровления попадает не в категорию защищённых, а в категорию восприимчивых, то есть может быть повторно заражён.
Дополнительно модель SIR имеет модификации, где учитывается врождённый иммунитет, или ситуации в которых выздоровевший может заражать других.
Модификация SIR — модель SIRVD
Модель SIRVD представляет собой расширенную версию модели SIR. В последнее время SIRVD часто используется в том числе и для моделирования пандемии COVID-19. Например в нашей статье используется SIRVD в комбинации с нейронной сетью для предсказания течения COVID-19, а здесь используется расширенная версия для оценки эффекта первой и второй дозы вакцины.
В этой модификации помимо восприимчивых, инфицированных и защищённых есть категории:
V (Vaccinated) – «вакцинированные»
D (Dead) – «умершие»
Ее можно представить в виде следующей системы уравнений:
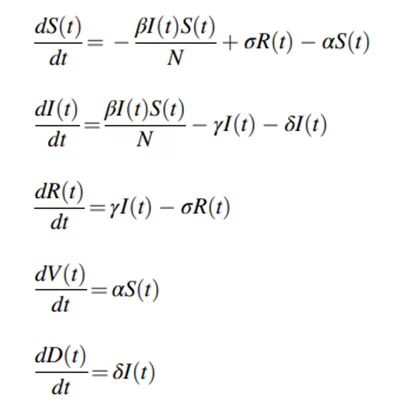
А в виде графика SIRVD выглядит так.
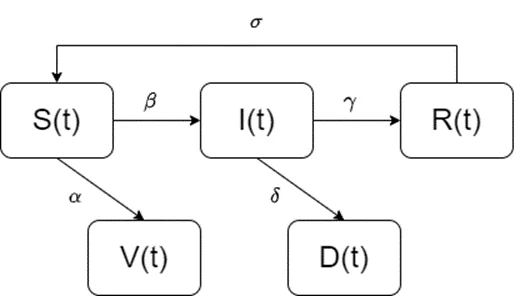
В данной модели категория Resistant в большей степени представляет собой категорию Recovered, так как после выздоровления не приобретается постоянный иммунитет, и становится возможным повторное заражение.
В отличие от SIR модель SIRVD имеет уже пять дополнительных параметров — это beta (скорость заражения), gamma (скорость выздоровления), alpha (скорость вакцинации), sigma (скорость потери иммунитета после перенесенного заболевания), delta (смертность).
Реализация модели SIRVD на Python
class SIRVD():
def __init__(self, S, I, R, V, D, beta=0.05, gamma=0.01, alpha=0.004, sigma=0.1, delta=0.01, epochs=365):
self.Susceptible = S
self.Infected = I
self.Recovered = R
self.Vaccinated = V
self.Dead = D
self.beta = beta
self.gamma = gamma
self.alpha = alpha
self.sigma = sigma
self.delta = delta
self.population = S + I + R + V + D
self.epochs = epochs
def start_simulation(self):
Susceptible = [self.Susceptible]
Infected = [self.Infected]
Recovered = [self.Recovered]
Vaccinated = [self.Vaccinated]
Dead = [self.Dead]
for epoch in range(1, self.epochs):
dS_dt = - (self.beta * Infected[-1] * Susceptible[-1]) / self.population + self.sigma * Recovered[-1] - self.alpha * Susceptible[-1]
dI_dt = (self.beta * Infected[-1] * Susceptible[-1]) / self.population - self.gamma * Infected[-1] - self.delta * Infected[-1]
dR_dt = self.gamma * Infected[-1] - self.sigma * Recovered[-1]
dV_dt = self.alpha * Susceptible[-1]
dD_dt = self.delta * Infected[-1]
Susceptible.append(Susceptible[-1] + dS_dt)
Infected.append(Infected[-1] + dI_dt)
Recovered.append(Recovered[-1] + dR_dt)
Vaccinated.append(Vaccinated[-1] + dV_dt)
Dead.append(Dead[-1] + dD_dt)
Комментарий: данную реализацию также можно оптимизировать, здесь она для наглядности приведена в соответствие с системой уравнений.
Если настроить параметры beta и gamma и количество восприимчивых и инфицированных как в модели SIR, а скорость вакцинации задать на 0.01 то можно увидеть следующую смоделированную эпидемию.
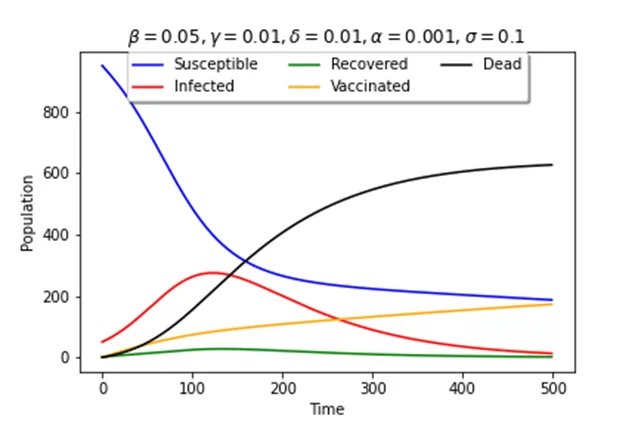
Число вакцинированных приближается к 25% популяции. Здесь видно, что максимальное число заражённых приближается к 300, что составляет почти треть всей здоровой популяции. Число умерших очень высоко и превышает 600.
Если повысить скорость вакцинации в модели, то можно увидеть следующий результат.
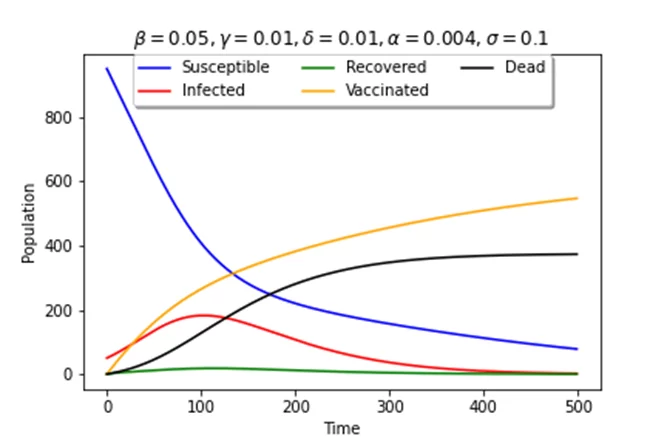
Число вакцинированных приближается к 50% популяции. Максимальное число инфицированных не превышает 200 человек, число умерших в сравнении с прошлой моделью снизилось на треть.
P.S.
Таким образом, модели с большей долей вероятности показывают значимую эффективность вакцинации в профилактике с заболеванием — при повышении процента вакцинации среди популяции значительно снижается число инфицированных и умерших. Если вам интересно узнать о более сложных и продвинутых моделях и о применении нейронных сетей для прогнозирования течения COVID-19, пишите в комментариях, ставьте лайки и мы обязательно расскажем об этом в следующих публикациях. Вакцинация помогает быстрее справиться с эпидемией, и является основным методом профилактики заболевания.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
