Время прочтения: 3 мин.
Анализ транзакций денежных средств может помочь экспертам выявить новые преступные схемы, а также недостатки в работе тех или иных процессов, связанных с переводами денежной наличности. Для работы с такими последовательностями используются графы и методы работы с ними.
В данной статье хотелось бы наиболее подробно остановиться на методах поиска компонента сильной связности графов, а также на том, как это может помочь в поиске «подозрительных» переводов и операций.
Немного теоретических тезисов:
Две вершины ориентированного графа называют сильно связанными, если есть путь из первой вершины во вторую и обратно.
Ориентированный граф можно назвать сильно связным, если каждая пара его вершин является сильно связной.
Так что же такое эта «компонента сильной связности» в графах, которые мы будем исследовать? Наиболее простой ответ на данный вопрос – «Это сильно связный подграф».
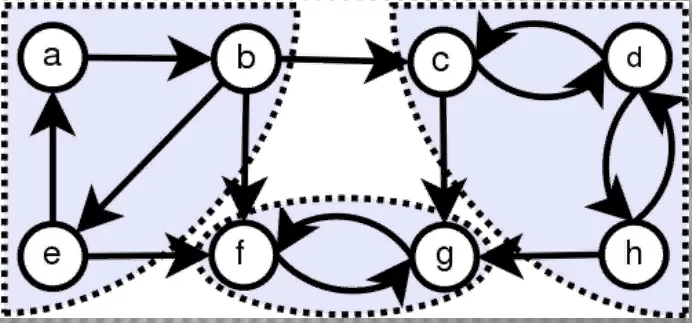
Для поиска компонент сильной связности будем использовать алгоритм Косарайю. Построим тестовый граф, как показано на рисунке:
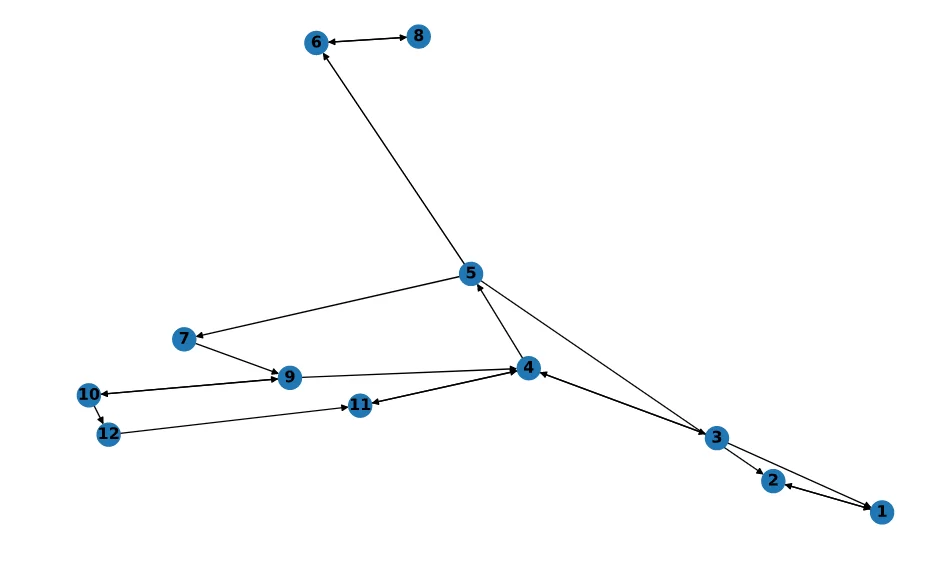
Для построения графа воспользуемся возможностями библиотек netwotkx и matplotlib, запустив следующий код:
import networkx as nx
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'svg'
plt.rcParams['figure.figsize'] = (10,6)
G = nx.DiGraph()
G.add_nodes_from(['1','2','3','4','5','6','7','8','9','10','11','12'])
G.add_edges_from([
('1','2'),('2','1'),('3','1'),('3','4'),
('4','3'),('4','5'),('4','11'),('5','2'),
('5','6'),('5','7'),('6','8'),('7','9'),
('8','6'),('9','10'),('9','4'),('10','9'),
('10','12'),('12','11')
])
nx.draw(G, with_labels=True, font_weight='bold')
Для полученного графа поиск компонент сильной связности по алгоритму Косарайю будет состоять из трёх шагов:
- Выполнить поиск в глубину, пока не будут «помечены» все вершины.
- Инвертировать исходный граф (сменить направление всех ребер в графе на противоположные).
- Выполнить поиск в глубину в порядке убывания пометок вершин.
Непосредственно код, выполняющий данные шаги:
# Считывание списка смежности вершин из текстового файла
def graph_to_vocab(adress):
graphs = {}
with open(adress) as file:
lines = file.readlines()
for line in lines:
line = line[:-1].split(' ')
graphs[line[0]] = line[1:]
return graphs
# Поиск пути из одной вершины в другую
def find_path(graph, start, end, path=[]):
path = path + [start]
if start == end:
return path
if start not in graph:
return None
for node in graph[start]:
if node not in path:
newpath = find_path(graph, node, end, path)
if newpath:
return newpath
return None
def connect(x1,x2):
return True if x1 != None and x2 != None else False
# Поиск компонент сильной связности
def Kosarai(graph_file):
abc = graph_to_vocab(graph_file)
graphs_list = []
for i in range(1,len(abc)+1):
res_graph = []
for j in range(1,len(abc)+1):
graph1 = find_path(abc, str(i), str(j))
graph2 = find_path(abc, str(j), str(i))
if connect(graph1, graph2):
if i!=j:
res_graph = graph1
if len(res_graph)>2:
graphs_list.append(res_graph)
return graphs_list
if __name__=="__main__":
print(Kosarai('graph.txt'))
Результат работы данного алгоритма для тестового графа:
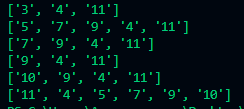
Найдем наиболее полные и уникальные списки смежности точек, по которым производятся переводы и отметим их в таблице:
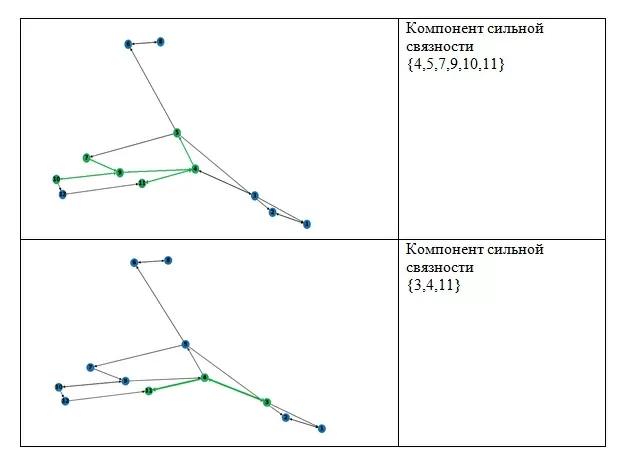
Как можно заметить из полученных подграфов, между данными транзакциями существуют устойчивые взаимоотношения по перечислениям, которые могут быть более подробно исследованы профильным сотрудником на предмет нарушений или реализации преступных схем.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
