Время прочтения: 5 мин.
При построении матриц миграции для анализа небольшого объема ссуд можно использовать Excel, но для оценки больших портфелей за несколько лет наблюдений необходимо использовать иные методы расчета, например, SQL/Python.
Коротко остановимся на процессе построения матриц миграции. На первом этапе осуществляется сегментации кредитного портфеля либо заемщиков по категориям качества ссудной задолженности. Могут использоваться различные варианты сегментации кредитного портфеля. Например, матрицы миграции могут строится по переходам субпортфеля/заемщиков по группам просрочки или рейтингам.
Элементы матрицы миграции представляют собой вероятность изменения рейтинга заемщика/группы просрочки за определенный временной интервал.
Например, для определенного субпортфеля на протяжении времени (например, месяц) анализируются переходы ссуд из одной группы просрочки другую. При этом задолженность может перейти как в худшую группу просрочки, так и в лучшую, а может остаться в этой же группе. Такая матрица показывает поведение заемщиков в течение анализируемого промежутка времени.
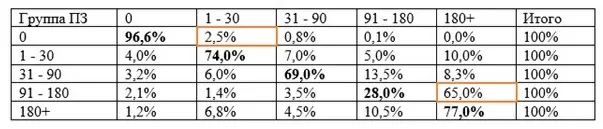
На примере, приведенном в таблице, видно, что с вероятностью 2,5% заемщики из группы «Без просроченных платежей» мигрируют в группу «Просрочка 1 – 30 дней», а заемщики, находящиеся в группе «Просрочка 91 -180 дней» с вероятностью 65% мигрируют в группу «Просрочка свыше 180 дней».
Большую роль в построении более точного прогноза играют актуальность данных и глубина анализируемого исторического периода. Чем больше анализируемый период, тем точнее прогноз, т.к. учитываются различные экономические, политические и иные факторы, оказывающие влияние на качество кредитного портфеля.
Для получения информации о переходах за весь исторический период (например, за 6 лет) значения матриц усредняются.
Так как с течением времени ссуды могут приобрести иные характеристики при первоначальном признании финансового актива Компания оценивает кредитный риск на 12 месяцев и на весь срок жизни актива. Для этого итоговые матрицы возводятся в степень равную периоду оценки кредитного риска (12 месяцев или срок жизни актива).
Рассмотрим код, с помощью которого мы построили матрицу миграции и возвели ее в степень 12.
На первом этапе с помощью языка SQL мы определили среднее значение доли заемщиков, которые на первую дату среза имели группу просроченной задолженности i, а на следующую дату среза перешли в группу просроченной задолженности j.
select
agg1.group1
,agg1.group2
,cast(summa_chisl/summa_znam as decimal(19,2)) sr_dol
from (
select group1
,group2
,sum(number) summa_chisl
from [basa].[matrix]
group by group1
,group2) agg1
left join (
select group1
,sum(number) summa_znam
from [basa].[matrix]
group by group1) agg2 on
agg1.group1 = agg2.group1
order by 1, 2
Далее в Python подключаемся к базе SQL и выполняем вышеуказанный скрипт:
import pyodbc
from sqlalchemy import create_engine
import pandas as pd
CONST_SERVER = ‘Server'
CONST_DATABASE = 'basa’
connection_str = r'Driver={SQL Server};Server=' + CONST_SERVER + ';DATABASE=' + CONST_DATABASE + ';Trusted_Connection=yes'
request = """
select
agg1.group1
,agg1.group2
,summa_chisl
,summa_znam
,cast(summa_chisl/summa_znam as decimal(19,2)) sr_dol
from (
select group1
,group2
,sum(number) summa_chisl
from [basa].[matrix]
group by group1
,group2) agg1
left join (
select group1
,sum(number) summa_znam
from [basa].[matrix]
group by group1) agg2 on
agg1.group1 = agg2.group1
order by 1, 2
"""
with pyodbc.connect(connection_str) as con:
engine = create_engine('mssql+pyodbc://', creator=lambda: con)
data = pd.read_sql(request, con)
В результате получаем среднюю долю мигрировавших за период заемщиков, сгруппированных по группам ПЗ:
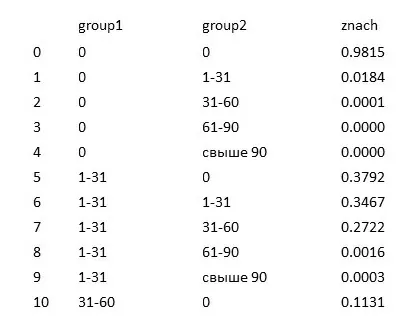
Далее данные из столбца «znach» переводим в numpy массив и меняем его размерность на (5, 5):
probabilities = data['znach']
probs = pd.DataFrame(probabilities)
numpy_array = probs.to_numpy()
numpy_array = numpy_array.reshape(5,5)
Получаем исходную матрицу со средними значениями по месячным переходам в течение исторического периода:
array([[9.815e-01, 1.840e-02, 1.000e-04, 0.000e+00, 0.000e+00],
[3.792e-01, 3.467e-01, 2.722e-01, 1.600e-03, 3.000e-04],
[1.131e-01, 1.307e-01, 2.570e-02, 7.269e-01, 3.600e-03],
[8.380e-02, 7.700e-02, 1.350e-02, 1.810e-02, 8.076e-01],
[8.100e-03, 4.000e-03, 7.000e-04, 5.000e-04, 9.868e-01]])
С помощью функции np.linalg.matrix_power(A, P), где А – матрица, P – степень, мы можем итоговую матрицу возвести в степень равную периоду оценки кредитного риска (12 месяцев или срок жизни актива). При этом, вместо непосредственного возведения в 12 степень, мы можем использовать цикл, в котором будем возводить исходную матрицу в степени от 1 до 12 и выводить результат на экран.
import numpy as np
table_columns = [
"0",
"1-30",
"31-60",
"61-90",
"90+",
]
for degree in range(1,13):
print(f"Месяц {degree}:")
result = np.linalg.matrix_power(numpy_array, degree)
result_dataframe = pd.DataFrame(result, columns=table_columns, index=table_columns)
result_dataframe = result_dataframe * 100
print(f"{result_dataframe}\n")
Результат будет следующим:
Месяц 1:
0 1-30 31-60 61-90 90+
0 98.15 1.84 0.01 0.00 0.00
1-30 37.92 34.67 27.22 0.16 0.03
31-60 11.31 13.07 2.57 72.69 0.36
61-90 8.38 7.70 1.35 1.81 80.76
90+ 0.81 0.40 0.07 0.05 98.68
Месяц 2:
0 1-30 31-60 61-90 90+
0 97.033084 2.445195 0.510920 0.010213 0.000588
1-30 53.457577 16.287911 10.142701 19.844601 0.267213
31-60 22.441914 10.673942 4.606401 3.204914 59.072865
61-90 12.103329 3.462637 2.212440 1.066776 81.162894
90+ 1.758110 0.561303 0.180511 0.101768 97.418176
Месяц 3:
………
Месяц 12:
0 1-30 31-60 61-90 90+
0 91.697332 2.860299 0.822638 0.617389 4.003870
1-30 68.381854 2.306220 0.682339 0.528402 28.124141
31-60 36.082358 1.520177 0.476558 0.387188 61.596381
61-90 22.423044 1.186051 0.388464 0.325778 75.764202
90+ 11.515956 0.920555 0.318920 0.277988 87.079001
Таким образом, используя в Python функциюnp.linalg.matrix_power(A, P) мы упростили задачу по возведению квадратной матрицы в необходимую степень. Матрица, возведенная в степень 12, описывает вероятность перехода на горизонте 12 месяцев, при этом значения колонки, соответствующей группе просрочки 90+, указывают на вероятность дефолта в течение года.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)
