Время прочтения: 5 мин.
Для реализации проекта мы использовали поквартальные данные финансовой отчетности заемщиков за год и выбран один из методов ML – xgboost, градиентный бустинг Python. Выбор метода для создания математической модели был обусловлен параметрами массива данных.
Исходные данные для создания обучающей выборки включали в себя финансовую отчетность 2913 клиентов за год, финансовое положение которых, по оценке кредитной организации, на начало года было хорошим. В качестве учителя мы использовали данные финансового положения клиентов, на основании оценки кредитной организации, на конец года.
Показатели финансовой отчетности клиентов являются количественными признаками за редким исключением, большинство из которых всегда имеют положительное значение. Информативность таких признаков, как отдельно взятых, довольно низкая, вследствие чего возникла необходимость преобразования признаков/создания новых комплексных признаков.
Для создания комплексных признаков в большинстве случаев был произведен расчет динамики признаков на основании данных 4 кварталов в относительных единицах измерения, в нашем случае были выбраны проценты. Динамическая составляющая признаков лежит в области положительных и отрицательных значений, данное свойство признаков несет в себе очень важную информацию о характеристике объекта в массиве. В процессе анализа простых признаков финансовой отчетности и разработки алгоритмов по созданию комплексных признаков, после предварительной обработки массива получили 19 комплексных признаков, из данных простых признаков финансовой отчетности.
Признаки были разработаны на основании нормативной финансово-экономической документации и ранее в нашей практике не использовались, необходимо было произвести их оценку влияния на характеристику объектов в массиве.
В качестве методов оценки признаков были выбраны инструменты: оценка важности признаков и коллинеарность признаков.
- Оценка качества модели
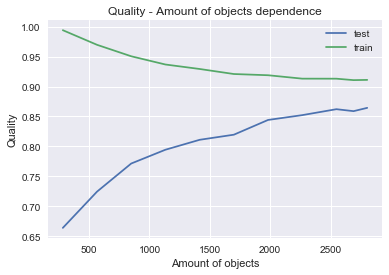
Оценка качества модели производилась с помощью метрики ROC_AUC в зависимости от количества объектов в выборке. По тренду графика оценки модели на тестовой выборке, можно сделать вывод о том, что при увеличении объектов в выборке качество модели растет.
ROC_AUC=0.863994043461
Значение метрики ROC_AUC хорошее. Проведем анализ признаков массива.
2. Анализ признаков
Первоначально обработанная выборка состояла из 15 комплексных признаков, после анализа признаков, описанного ниже, тест прошли 12 признаков, 3 признака были отвергнуты по причине их относительной важности равной нулю или близкой к этому значению.
#модель XGBoost автоматически рассчитывает важность признаков для задачи прогнозного моделирования.
#Эти оценки важности доступны в feature_importances_.
#они могут быть напечатаны следующим образом:
print(model.feature_importances_)
[ 0.15873016 0.09977324 0.16439909 0.12811792 0.08163265 0.07709751
0.06462585 0.07936508 0.13038549 0.00226757 0.01133787 0.00226757]
#plot
#Выведем эти оценки непосредственно на гистограмму, чтобы получить визуальное представление об
#относительной важности каждого объекта в массиве данных.
plt.bar(range(len(model.feature_importances_)), model.feature_importances_)
plt.show()
#Недостатком этого графика является то, что объекты упорядочены по их входному индексу,
#а не по важности. Можно отсортировать признаки по значениям важности, прежде чем строить гистограмму.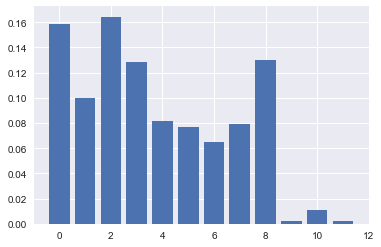
#В предыдущей гистограмме отсутствует легенда признаков и как следствие её наглядность оставляет желать лучшего.
#В список labels запишем названия признаков
#Так как названия признаков довольно длинные, построим горизонтальную гистограмму
position = np.arange(12)
fig, ax = plt.subplots()
ax.barh(position, model.feature_importances_)
#Устанавливаем позиции тиков:
ax.set_yticks(position)
#Устанавливаем подписи тиков
ax.set_yticklabels(labels,
fontsize = 15)
fig.set_figwidth(10)
fig.set_figheight(6)
plt.show()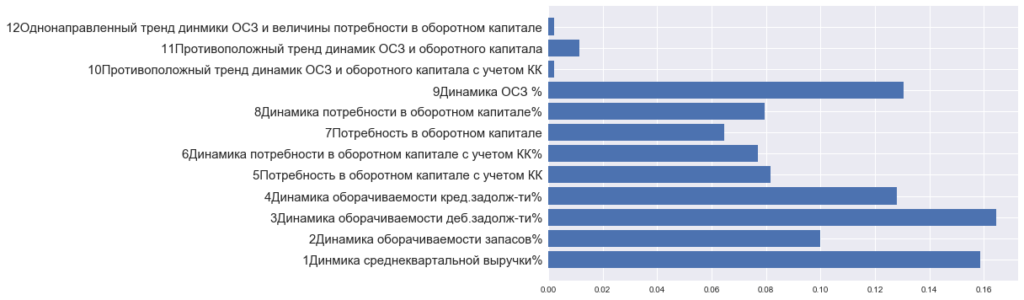
На гистограмме можно заметить пару признаков, исходя из смыслового содержания названий которых напрашивается вывод, что один из этих признаков, возможно, лишний. Это признаки «5Потребность в оборотном капитале с учетом краткосрочных кредитов» и «7Потребность в оборотном капитале». Чтобы проверить нашу гипотезу обратимся к инструменту, который дает оценку попарной корреляции признаков в массиве:
#8. Диаграмма корреляции
#Диаграмма корреляции используется для визуального просмотра метрики корреляции между всеми возможными парами числовых
#переменных в массиве.
plt.figure(figsize=(12,10), dpi= 100)
sns.heatmap(tab_new.corr(), xticklabels=tab_new.corr().columns, yticklabels=tab_new.corr().columns, cmap='RdYlGn', center=0, annot=True)
plt.title('Correlogram of Data_FO', fontsize=22)
plt.xticks(fontsize=10)
plt.yticks(fontsize=10)
plt.show()
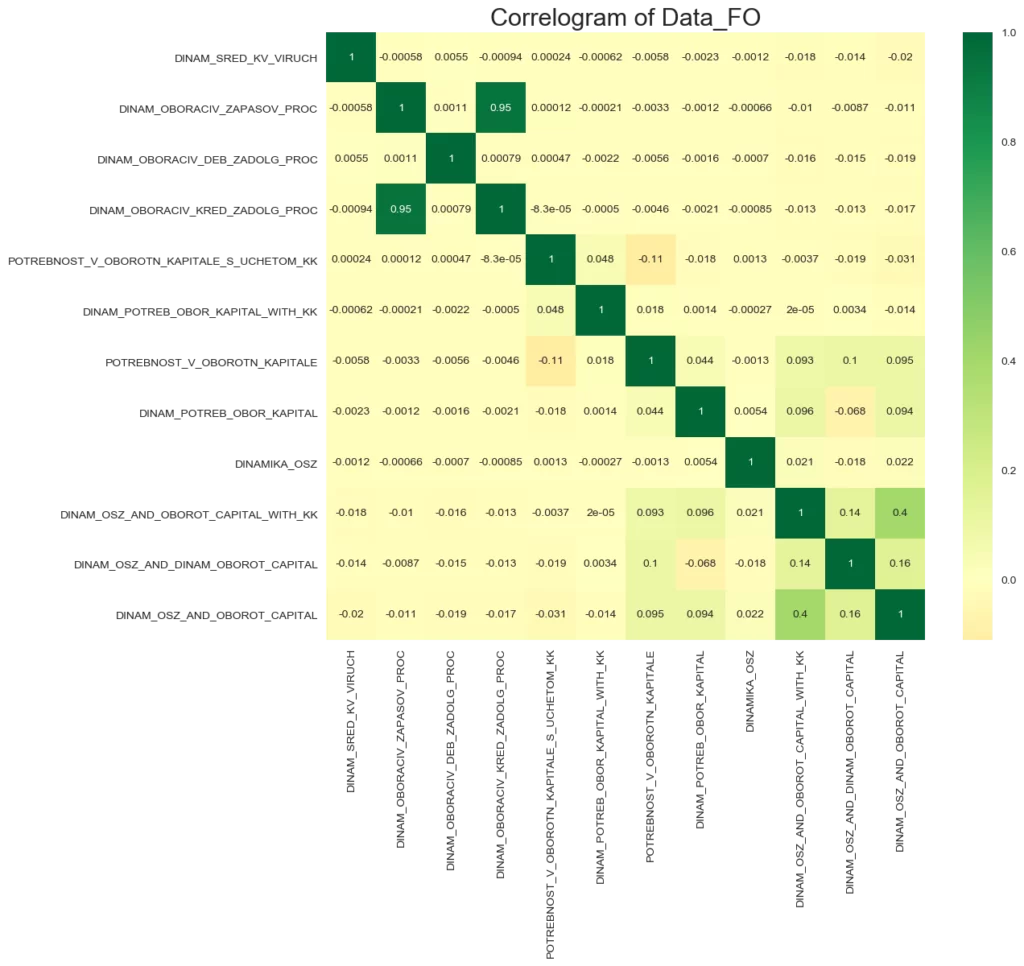
Коэффициент корреляции признаков «5Потребность в оборотном капитале с учетом КК» и «7Потребность в оборотном капитале» равен 0.0014. Корреляция признаков оказалась минимальной. Следовательно, данные признаки существенно отличаются по характеру оценки объектов в массиве, удалять из массива признаки нецелесообразно.
Также инструмент оценки корреляции выявил два признака с высокой степенью корреляции, равной 0.95. На практике, если коэффициент корреляции больше 0.98, рекомендуется один из парных признаков удалять из массива. В нашем случае этот порог не превышен, но для чистоты эксперимента удалим один из парных признаков с высокой степенью корреляции. Обучим модель на новой выборке. Оценим точность модели метрикой ROC_AUC.
ROC_AUC=0.858798142457
Качество модели понизилось, следовательно, удаление признака с высокой степенью корреляции нецелесообразно.
Вернемся к анализу важности признаков в выборке. Признаки «10Противоположный тренд динамик ОСЗ и оборотного капитала с учетом КК», «11Противоположный тренд динамик ОСЗ и оборотного капитала», «12Однонаправленный тренд динамики ОСЗ и величины потребности в оборотном капитале» были созданы на данных довольно большого количества простых признаков финансовой отчетности. Алгоритм создания комплексных признаков был разработан с командой аналитиков. На практике, как оказалось, эти признаки имеют довольно низкую относительную важность по сравнению с остальными признаками. На основании данного заключения мы приняли решение не удалять данные признаки из массива, так как важность признаков рассчитана на основании данных массива, выбранного из определенного промежутка времени. В будущих периодах характеристики объектов могут измениться под воздействием внешних и внутренних экономических и политических факторов и при переобучении модели на новом массиве, важность факторов может кардинально измениться.
В статье дано описание только некоторых аспектов одновременного использования таких инструментов Python, как оценка важности признаков и коллинеарность признаков. Можно найти еще довольно много интересных возможностей при одновременном использовании данных инструментов.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
