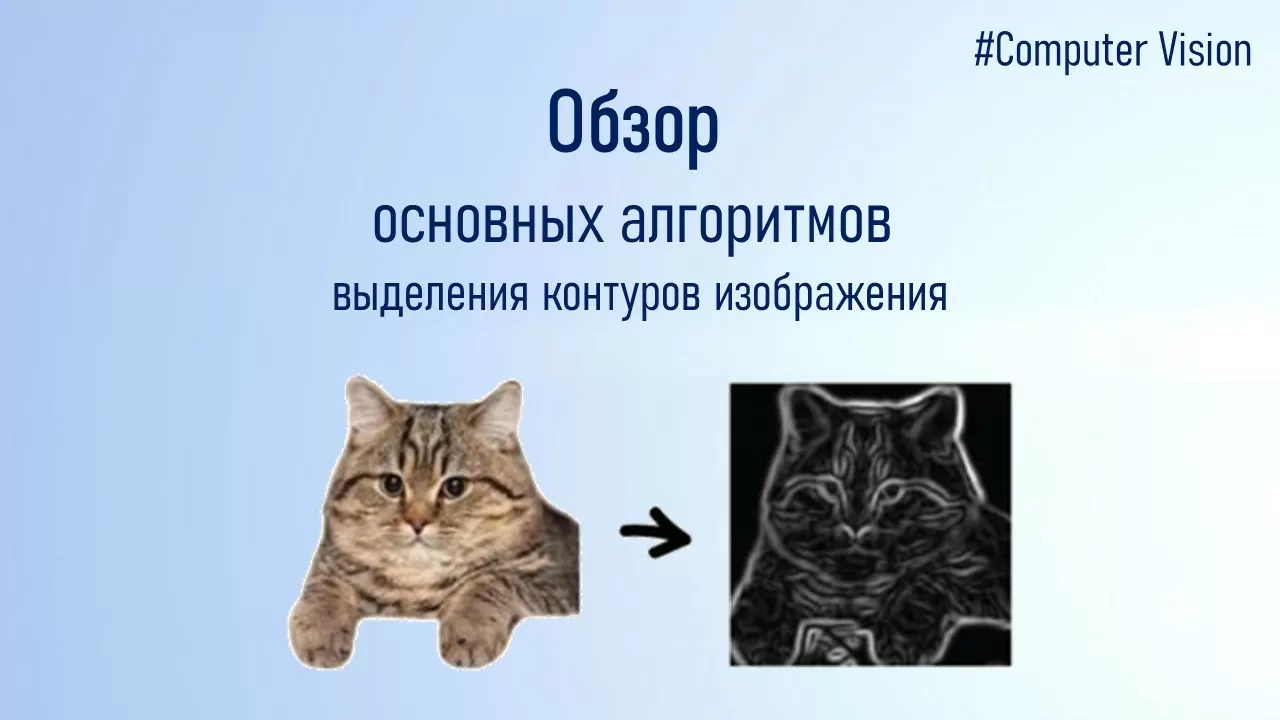
Время прочтения: 6 мин.
Для начала рассмотрим понятия фильтра и пространственной фильтрации.
Пространственная фильтрация изображения – это метод, при котором каждая точка изображения последовательно обрабатывается с помощью оператора, представленного в виде квадратной матрицы. Результатом работы этого метода является оценка значимости каждого пикселя изображения. Одним из признаков значимости пикселей являются резкие перепады яркости.
Изображение представляет собой двумерную функцию пространственных координат. Обычно эта функция обозначается как f(x,y). Пусть имеется некое изображение в системе координат XY. Рассмотрим произвольную точку с координатами (x,y) и 3×3 — окрестность этой точки.
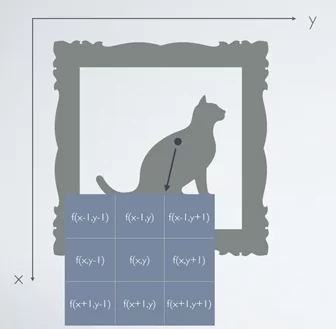
Фильтр представляет собой некую квадратную матрицу w, размер которой соответствует размеру окрестности обрабатываемой точки. Отклик фильтра вычисляется для каждой точки изображения с координатами (x,y). Рассмотрим пример линейной пространственной фильтрации. Для точки (x,y) значение отклика фильтра R будет вычисляться следующим образом: каждый элемент окрестности точки (x,y) последовательно умножается на соответствующий элемент маски фильтра. Затем полученные значения суммируются.
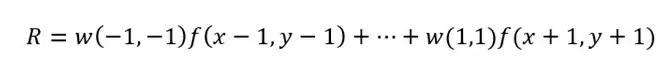
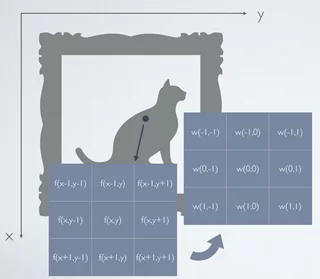
Коэффициенты фильтра вычисляются на основе дифференцирования амплитуды сигнала. Так как производная – это отношение приращения функции к приращению аргумента, а в случае изображения приращение аргумента будет всегда равно единице, то есть одному пикселю, то это эквивалентно разности значений яркости соседних пикселей:
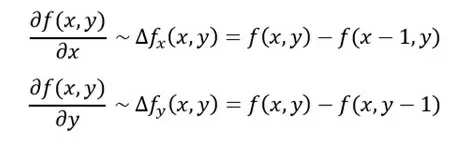
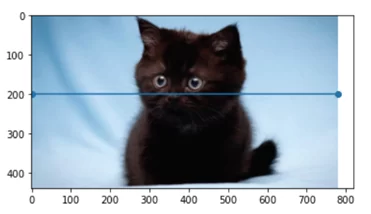
Рассмотрим пример. Возьмем черно-белое изображение.
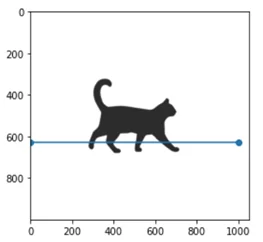
Построим график значений яркости пикселей, расположенных на линии. Так как изображение не содержит шума, то на графике четко видны очертания четырех лапок кошки.
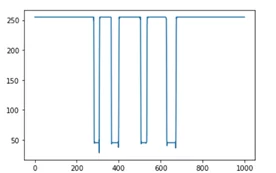
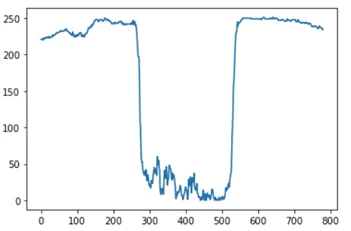
А теперь построим график производной по x по графику яркости. С помощью данного графика видно, в каких точках были резкие перепады яркости, соответственно, в этих точках проходят контуры изображения.
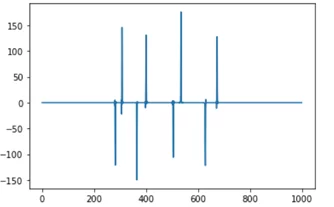
Теперь возьмем цветное зашумленное изображение и построим для него такие же графики для пикселей, расположенных на линии.
На графике яркости пикселей контуры прослеживаются уже не так очевидно, так как в данном случае мешают шумы, неоднородная текстура изображения.
На графике производной определить контуры также затруднительно.
Оператор Робертса
Рассмотрим 3×3 окрестность пикселя изображения:
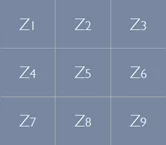
Оператор Робертса является одним из первых и самых простых способов нахождения частных производных. Рассмотрим точку Z5 и вычислим частные производные с помощью оператора Робертса. Так как данный оператор является перекрестным, то и производные вычисляются как перекрестная разность элементов.
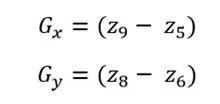
где и – это частные производные по x и по y соответственно
Оператор Робертса предполагает следующие фильтры:
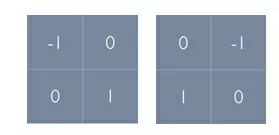
Оператор Робертса проигрывает в качестве выделения контуров по сравнению с другими операторами. Фильтры размерности 2х2 существенно снижают качество результата, так как нет четко выраженного центрального элемента. Также данный оператор очень чувствителен к шуму. Но несмотря на его недостатки, оператор Робертса все еще используется, так как скорость обработки изображения с помощью него довольно высока.
Оператор Прюитта
В данном операторе будем также рассматривать 3×3 окрестность пикселя изображения. В этом случае формулы для вычисления частных производных:
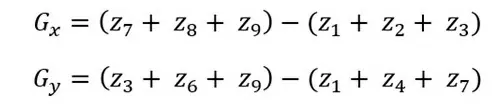
Так как в случае изображения производная равна дискретной разности, то в данных формулах приблизительное значение производной по оси x вычисляется как разность сумм значений элементов верхней и нижней строки, а разность сумм значений элементов по первому и последнему столбцам этой окрестности – производной по оси y.
Для реализации этих формул используется линейная пространственная фильтрация со следующими масками-фильтрами:
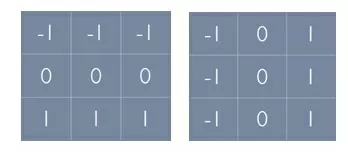
Оператор Собеля
Оператор Собеля определяется фильтрами, очень схожими с фильтрами оператора Прюитта. Он отличается в использовании весового коэффициента 2 для средних элементов:
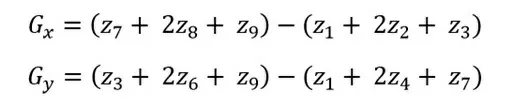
Этот коэффициент используется для уменьшения эффекта сглаживания за счет придания большего веса средним точкам.
Маски оператора Собеля:

Реализация оператора Собеля на python
На данном листинге реализована функция, которая возвращает приблизительное значение градиента в точке с помощью оператора Собеля.
def getsobel(x,y):
# Вычисляем значения яркости пикселей в 3x3 окрестности точки с координатами (x,y)
z1 = getpixel(x-1,y-1)
z2 = getpixel(x,y-1)
z3 = getpixel(x+1,y-1)
z4 = getpixel(x-1,y)
z5 = getpixel(x,y)
z6 = getpixel(x+1,y)
z7 = getpixel(x-1,y+1)
z8 = getpixel(x,y+1)
z9 = getpixel(x+1,y+1)
# Вычисляем значения частных производных
G_x = z7 + 2*z8 + z9 - (z1 + 2*z2 + z3)
G_y = z3 + 2*z6 + z9 - (z1 + 2*z4 + z7)
# Возвращаем значение градиента в точке с координатами (x,y)
return sqrt(G_x ** 2 + G_y ** 2)
Видно, что изображение не имеет четких краев из-за его зашумленности.

Эту проблему можно частично решить с помощью порога на значение градиента, определяемого оператором Собеля. Стоит учитывать, что чем выше порог, тем выше вероятность потери важных границ объекта изображения.

Также можно реализовать данный метод с помощью библиотеки OpenCV:
def sobel_edge_detection(img):
a = 0
b = 1
c = 2
f_x = np.array([[-b, -c, -b],[a, a, a],[b, c, b]])
f_y = np.array([[-b, a, b],[-c, a, c],[-b, a, b]])
res = cv2.filter2D(img,-1,f_x) + cv2.filter2D(img,-1,f_y)
return res
imshow(img_r, filter_=sobel_edge_detection)
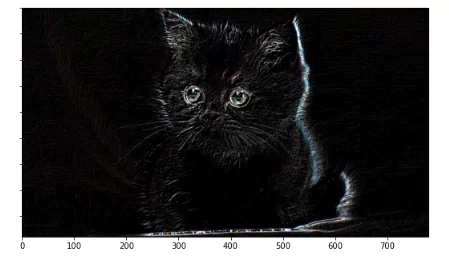
Реализацию остальных операторов можно посмотреть на GitHub по ссылке
Рассмотренные методы выделения контуров изображения хорошо работают в том случае, когда изображение имеет однородную текстуру и в нем отсутствуют шумы. Если эти условия не соблюдаются, то данными методами обнаружатся также лишние границы, которые будет сложно отделить от основного объекта. Для каждого изображения эти методы требуют ручной настройки пороговых значений из-за различных условий съемки изображений, например, освещенности. Поэтому применение этих методов довольно ограничено. В нейронных сетях выделение границ и прочих локальных характеристик производится в первичных сверточных слоях (Conv2D), т.е. сверточный слой соответствует маске фильтра. Определение значений маски w производится в процессе обучения нейронной сети.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)