Время прочтения: 5 мин.
В этой статье я расскажу, что такое выбросы, как их обнаружить и что можно предпринять в их отношении перед построением модели.
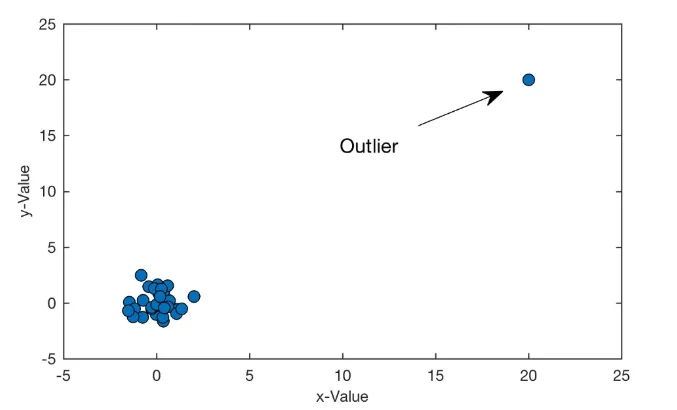
Выбросы (англ. outliers) – объекты, значения признаков которых сильно отличаются от признаков основной массы объектов. То есть это объекты, сильно выпадающие из общей картины.
Откуда же берутся выбросы? Во-первых, появление выбросов может быть обусловлено технической стороной эксперимента (например, в процессе сбора данных сменилось оборудование или у прежнего изменилась чувствительность датчиков). Во-вторых, на появление выбросов может влиять человеческий фактор. Возможны и другие причины: изменение правил проведения эксперимента, какая-то случайность или действительно уникальное значение.
В любом случае, какой бы ни была причина появления выбросов, они мешают алгоритмам обучаться, т.е. не дают построить хорошее решающее правило. Конечно, существуют алгоритмы машинного обучения (робастные), которые сами удачно обрабатывают выбросы. Но большинство алгоритмов путается в выбросах, пытается предсказать соответствующее значение для них, а в итоге плохо предсказывает значения как для выбросов, так и для остальных значений. Поэтому для получения хорошего решающего правила для основной массы объектов рекомендуется выявлять аномалии и обрабатывать их.
Так как же обнаружить аномальные явления в данных? Можно, конечно, это сделать визуально. Но для этого нужно располагать хорошими знаниями в предметной области, что не всегда возможно. Я расскажу про два способа, которые берут за основу распределение данных. Импортируем необходимые для обработки данных библиотеки:
import pandas as pd
import seaborn as sns
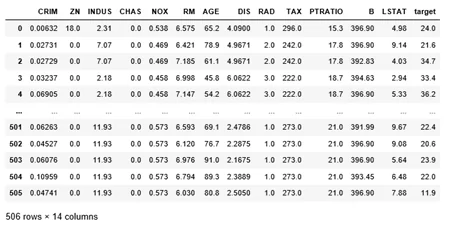
Для рассмотрения методов воспользуемся встроенным датасетом Boston библиотеки Scikit-learn. Он содержит набор данных о жилье в Бостоне (506 объектов, 13 признаков, целевая переменная – цена за дом).
from sklearn.datasets import load_boston
dataset = load_boston()
df = pd.DataFrame(dataset.data, columns = dataset.feature_names)
df['target'] = dataset.target
Для начала рассмотрим признак ‘RM’ – количество комнат в доме. Построим «ящик с усами» или бокс-диаграмму. Это один из способов визуального представления распределения. Нижний и верхний концы ящика соответствуют 1-му и 3-му квартилям (25% и 75% квантилям соответственно), а горизонтальная линия внутри ящика – медиане. Верхний «ус» продолжается вверх вплоть до максимального значения, но не выше полуторного межквартильного расстояния от верхней кромки ящика. Аналогично нижний ус продолжается вниз до минимального значения, но не ниже полуторного межквартильного расстояния от нижней кромки ящика. Концы «усов» обозначаются небольшими горизонтальными линиями. А за пределами усов значения изображаются в виде отдельных точек – эти значения можно считать выбросами.
figure=df.boxplot(column='RM')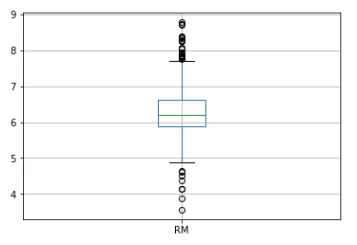
Также воспользуемся графиком distplot, который показывает и гистограмму, и график плотности одновременно.
sns.distplot(df['RM'].dropna())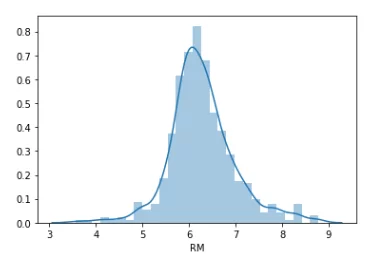
Как видно по графику данные в столбце ‘RM’ распределены нормально. Воспользуемся следующей формулой для определения границ выбросов:
Нижняя граница = Среднее значение – 3 * Стандартное отклонение
Верхняя граница = Среднее значение + 3 * Стандартное отклонение
lower_bound = df['RM'].mean()-3*df['RM'].std()
upper_bound = df['RM'].mean()+3*df['RM'].std()
print(lower_bound, upper_bound)
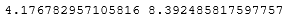
Таким образом, все значения меньшие, чем 4.1768 и большие, чем 8.3925 будут считаться выбросами.
Теперь рассмотрим данные из столбца ‘DIS’ (взвешенные расстояния до пяти бостонских центров занятости). Выведем аналогичные графики.
figure=df.boxplot(column='DIS')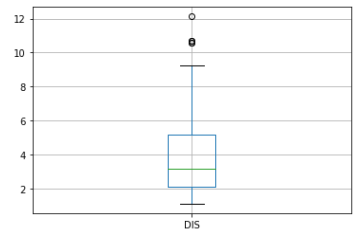
sns.distplot(df['DIS'].dropna())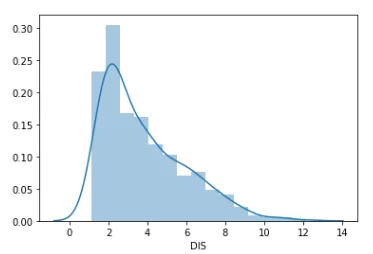
Как видно из графика данные перекошены в левую сторону, и предыдущий способ к ним не подходит. Воспользуемся ниже приведенными формулами для нахождения аномальных значений:
Нижняя граница = Первый квартиль – 1.5 * Межквартильное расстояние,
Верхняя граница = Третий квартиль + 1.5 * Межквартильное расстояние,
Межквартильное расстояние (IQR) = 75% квантиль – 25% квантиль
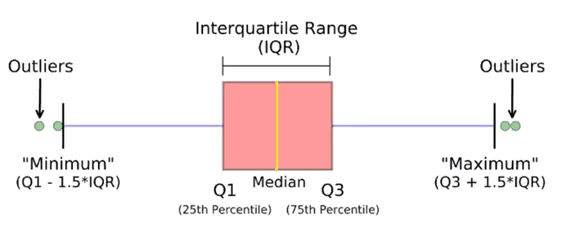
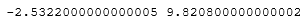
В случае, когда выбросы находятся чрезвычайно далеко от границ выбросов, используют следующую формулу:
Нижняя граница = Первый квартиль – 3 * Межквартильное расстояние,
Верхняя граница = Третий квартиль + 3 * Межквартильное расстояние
lower_bound = df['DIS'].quantile(0.25)-3*IQR
upper_bound = df['DIS'].quantile(0.75)+3*IQR
print(lower_bound, upper_bound)
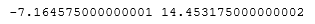
Теперь мы знаем, как определить выбросы, но что же делать с ними в дальнейшем? Конечно, можно удалить все аномальные значения, и это не вызовет особых проблем при работе с исчерпывающим датасетом в несколько десятков тысяч строк. Но что делать, если у вас немного данных? Один из вариантов решения – заменить аномальные значения на значение границ.

/img/star (2).png.webp)





/img/news (2).png.webp)
/img/event.png.webp)