Время прочтения: 4 мин.
Способность распознавать прямые линии важна как в человеческом, так и в компьютерном зрении. Человек может легко распознать многие типы объектов и их положения, просто увидев силуэт или грубый набросок. Обучить систему тому же – задача распознавания изображений. И определение прямых линий – важная часть этой задачи. Способов решения таких задач много. В этой статье я расскажу о преобразовании линии Хафа. Как это работает?
Прямую в пространстве изображения можно выразить двумя переменными. Например:
- В декартовой системе координат: Параметры: (m, b).
- В полярной системе координат: Параметры: (r, θ)
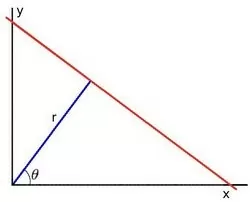
Для преобразований Хафа мы выразим линии в полярной системе. Следовательно, линейное уравнение можно записать как:
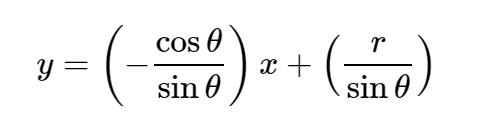
В общем, для каждой точки (x0, y0) мы можем определить семейство линий, проходящих через эту точку, как:
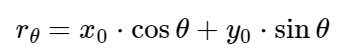
Это означает, что каждая пара (rθ, θ) представляет каждую линию, проходящую через (x0, y0).
Если для заданного (x0, y0) мы построим семейство линий, которые проходят через него, мы получим синусоиду. Например, для x0 = 8 и y0 = 6 получаем следующий график (в плоскости θ — r):
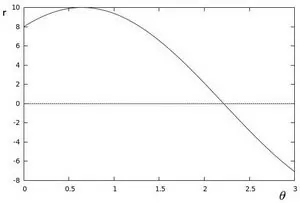
Мы рассматриваем только такие точки, что r> 0 и 0 <θ <2π.
Мы можем проделать ту же операцию для всех точек изображения. Если кривые двух разных точек пересекаются в плоскости θ — r, это означает, что обе точки принадлежат одной прямой. Например, следуя приведенному выше примеру и рисуя график еще для двух точек: x1 = 4, y1 = 9 и x2 = 12, y2 = 3, мы получаем:
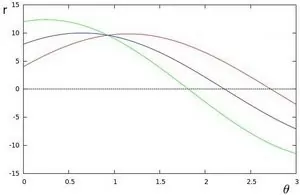
Три графика пересекаются в одной точке (0.925, 9.6), эти координаты являются параметрами (θ, r) или линией, в которой лежат (x0, y0), (x1, y1) и (x2, y2).
Что означает все вышеперечисленное? Это означает, что в целом линию можно обнаружить, определив количество пересечений между кривыми. Чем больше пересекающихся кривых, тем больше точек на линии, представленной этим пересечением. В общем, мы можем определить порог минимального количества пересечений, необходимых для обнаружения линии.
Это то, что делает метод преобразования линии Хафа. Он отслеживает пересечение кривых каждой точки изображения. Если количество пересечений превышает некоторый порог, то он объявляет это как линию с параметрами (θ, rθ) точки пересечения.
В библиотеке OpenCV существует два типа нужного нам алгоритма, а именно стандартное преобразование линии Хафа и вероятностное преобразование линии Хафа. Стандартный даст нам уравнение линии, поэтому мы не знаем начало и конец линии. В то время как вероятностное линейное преобразование даст список строк, в котором строка является списком начальной и конечной координаты. Для примера применения данного алгоритма возьмём задачу распознавания границ ячеек в таблице. Для такой задачи вероятностный вариант предпочтительнее. Так же разделим горизонтальные и вертикальные линии.
canny = cv.Canny(img, 50, 150)
cImg = np.copy(img)
houghLines = cv.HoughlinP(canny, 1, 1*np.pi/180, 40 , 250 , None, 250, 6 )
lin_horiz = []
lin_vert = []
if houghLines is not None:
for i in range(0, len(houghLines))
lin = houghLines[i][0]
if (lin[0]==lin[2]):
lin_vert.append(l)
elif (lin[1]==lin[3]):
lin_horiz.append(l)
for i, lin in enumerate(lin_horiz):
cv.lin(cIm, (lin[0], lin[1]), (lin[2], lin[3]), (0,255,0), 3, cv.lin_AA)
for i, lin in enumerate(lin_vert):
cv.lin(cIm, (lin[0], lin[1]), (lin[2], lin[3]), (0,0,255), 3, cv.lin_AA)
cv.imshow("with_line", cIm)
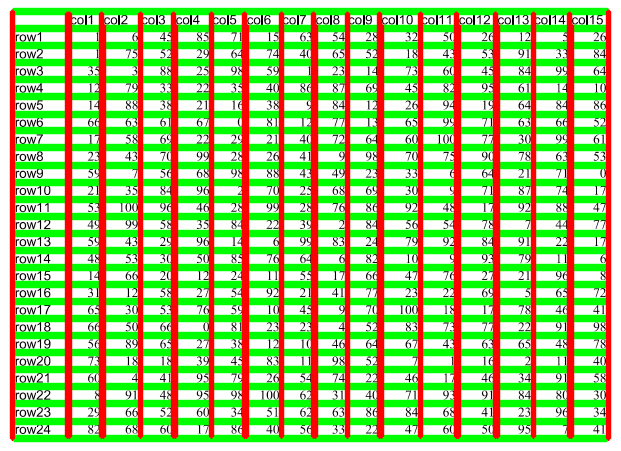
Полученный список координат обнаруженных линий в дальнейшем может помочь распознать содержимое таблицы точнее, вырезая содержимое ячейки и распознавая его в отдельности от остального изображения.

/img/star (2).png.webp)




/img/news (2).png.webp)
/img/event.png.webp)
